43

В.Н. Фальк

ВВЕДЕНИЕ В СЕТИ ПЕТРИ

И МОДЕЛИРОВАНИЕ СИСТЕМ

Учебное пособие

Москва 2009

1. Сети Петри. Основные понятия.

Сети Петри [1,2] – формальная модель поведения многоагентных систем, основанная на понятиях события и ресурса. Процесс в системе рассматривается как последовательность событий. Для возникновения событий необходимы ресурсы, а в результате событий возникают новые ресурсы.

Наиболее компактное формальное определение сети Петри может быть дано с использованием понятия комплекта элементов некоторого (базового) множества. Комплект¹ элементов множества (синонимом является понятие мультимножества) можно определить различными способами. Во-первых, его можно определить как конечный неупорядоченный набор элементов базового множества . Во-вторых, комплект можно определить как функцию, такую, что, определяющую для каждого элемента базового множествакратность его вхождения в соответствующий неупорядоченный набор. Наконец, если базовое множество конечно, то можно задать на нем некоторый линейный порядок и представить его как конечное упорядоченное множество . В этом случае комплект можно определить как кортеж длиныкратностей вхождения элементов базового множества:. На множестве комплектов базового множества можно определить различные бинарные отношения и операции, возможно, частичные. Мы будем использовать такие:

,

,

,

,

.

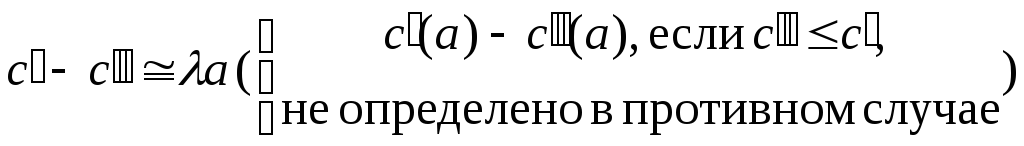Сетью Петри принято называть тройку , где– граф сети Петри, – конечное множествопозиций (или мест) сети, – конечное множествопереходов сети, ;– функции, задающие комплектывходных и, соответственно, выходных позиций переходов сети (здесь – множество всевозможных конечныхкомплектов элементов множества );– множество всевозможных состояний сети (маркировок); –начальная маркировка сети, задающая начальное состояние сети, –функция раскраски, возможно частичная, где – множествокрасок.

Позиции представляют виды ресурсов, маркировка определяет состояние системы – для каждой позиции задает количество единиц данного ресурса в данном состоянии. Переходы представляют возможные события в системе: входные связи перехода с позициями определяют необходимые для события ресурсы, а выходные – создаваемые в результате события ресурсы.

Пользуясь терминологией теории графов, можно сказать, что сети Петри – двудольные мультиорграфы с вершинами двух сортов (позициями, помеченными натуральными числами согласно начальной маркировке, и переходами, помеченными элементами множества согласно функции раскраски). Позиции как вершины графа изображаются в форме кружков, а переходы – в форме линий («полок»), обычно утолщенных (рис. 1). В кружке, соответствующем позиции , значениеизображается либо в форме соответствующего количества жирных точек («фишек»), либо в виде выражения (терма), определяющего значение. Метки переходов изображаются рядом с соответствующими «полками».

Если множество возможных красок конечно, то оно рассматривается как некоторый алфавит. Вследствие этого последовательность «срабатывающих» переходов представляет собой слово в этом алфавите, а множество возможных последовательностей образует формальный язык в алфавите. Основанная на этих понятиях семантика сетей Петри рассматривается более подробно в соответствующем разделе. Если, а– тождественная функция, то сеть Петри называетсясвободно раскрашенной.

Сети Петри рассматриваются с точностью до изоморфизма, то есть имена позиций и переходов являются «связанными» внутри сети и при графическом изображении, вообще говоря, могут не указываться (они необходимы только для ссылок, например, при описании поведения сети):

Определение 1. Сети и, считаютсяидентичными, если существуют взаимно-однозначные отображения и, такие, что

.

Основой определения операционной семантики сетей Петри является функция переходов , в общем случае частичная:

Функция обобщается на множество кортежей переходов::

,

Множество маркировок, достижимых из маркировки , обозначается и определяется так: , а множество всех достижимых в сети маркировок (достижимых из начальной маркировки ) так: . Маркировка называетсятупиковой, если для всех не определено, т.е. не выполняется условие.обозначает подмножество всехдостижимых тупиковых маркировок в сети. Кортеж переходов называется историей достижения в сети маркировки , если. Множество всех возможных историй достижения маркировкиобозначим.

Задачи исследования операционной семантики сетей Петри можно разделить на две группы: задачи анализа активности переходов и задачи анализа достижимости маркировок.

Приведем одну из возможных классификаций переходов по степени их активности (переход имеет данный уровень активности, если он удовлетворяет указанным требованиям и не отвечает требованиям более высокого уровня активности):

1. не выполняется условие срабатывания ни в одной из достижимых маркировок («мертвый» переход, не встречается ни в одной истории достижения маркировок из );

2. выполняется условие срабатывания хотя бы в одной из достижимых маркировок («потенциально живой» переход, встречается хотя бы в одной истории достижения маркировок из 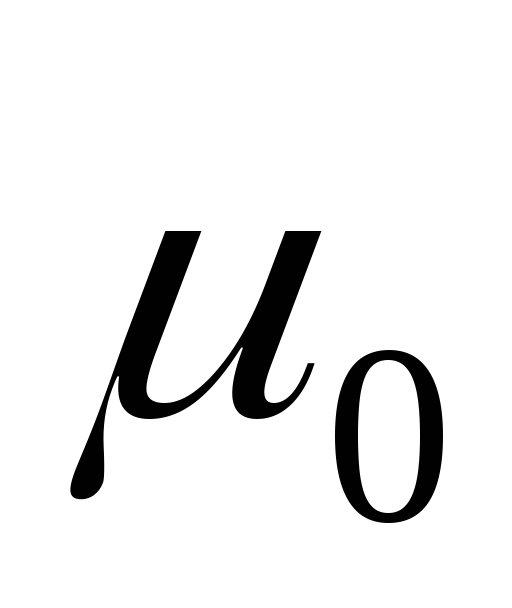, причем одновременно и «потенциально мертвый», т.е. существует достижимая маркировка, ни в одно из продолжений истории ее достижения которой он не входит);

3. для любого заданного натурального числа 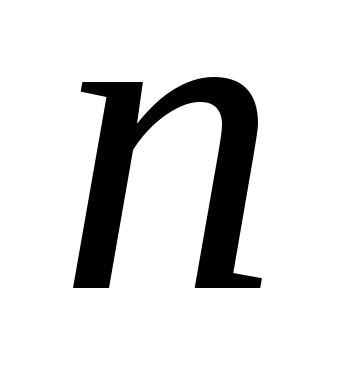существует история достижения маркировки из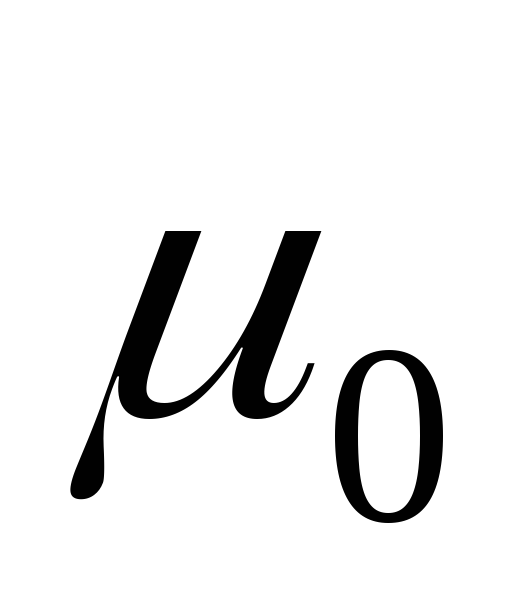, в которую переход входит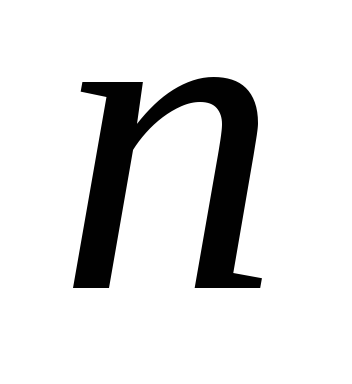раз;

4. существует потенциально бесконечная история поведения сети, в которую переход входит потенциально бесконечное (т.е. любое) число раз;

5. для любой достижимой маркировки существует продолжение истории поведения сети, в которую входит рассматриваемый переход («вечно живой» переход).

На рис. 2 приведена сеть, переходы которой перечислены в соответствии со степенью их активности.