Паросочетания в двудольных графах.

Определение 4.

Паросочетанием в любом графе называется подмножество попарно не смежных рёбер.

Определение 5.

Паросочетания в двудольном графе называются совершенными, если для любой вершины из левой или правой доли инцидентное ей ребро входит в это паросочетание.

Определение 6.

Максимальное паросочетание имеет максимальное число рёбер.

Следствие.

–множество всех вершин из Y, смежных с z. Если существует совершенное паросочетание, то

Необходимое и достаточное условие.

Определение 7.

Пусть – двудольный граф,. Произвольно занумеруем рёбра. Возьмём матрицу:

Пример.

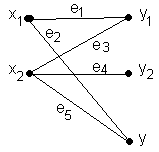
Определение 8.

Перманент квадратной матрицы А – сумма модулей всех слагаемых определителей .

Утверждение.

Все совершенные паросочетания в двудольном графе однозначно соответствуют ненулевым слагаемым в.

Ненулевое слагаемое имеет вид . Покажем, чтопопарно смежны, т. е. образуют паросочетание. Еслиисмежны в вершине доли(или долиY), то слагаемое перманента, содержащее такие рёбра, соответствует выбору одинаковых строк (одинаковых столбцов) матрицы , что невозможно по определению перманента и определителя.

Теорема 1. (Холла, критического существования совершенного паросочетания)

В двудольном графе существует совершенное паросочетание



Уже доказано выше.

Пусть это условие выполняется, но совершенное паросочетание не существует, тогда каждое слагаемое равно 0. Для любой подстановки .

Пусть , тогдастрокподматрица изp строк , у которой любой минор порядкаp равен 0(получили противоречие). 

Пример.

Следствие. (достаточное условие существования совершенного паросочетания)

Пусть .

Если , то совершенное паросочетание существует.

Пусть , рассмотрим– множество рёбер, инцидентных вершинам изz.

Пусть



Следствие.

Если , то существует совершенное паросочетание.

Лекция № 9.

СПОСОБЫ ПОСТРОЕНИЯ

СОВЕРШЕННОГО ПАРОСОЧЕТАНИЯ.

1. Условия теоремы Холла (самый не эффективный).

2. С помощью перманента (универсальный).

Венгерский алгоритм:

Обозначим паросочетания за П («пи»);

Рёбра, входящие в П назовём Т-рёбрами (тёмными);

Остальные рёбра назовём С-рёбрами (светлыми).

1. Начать с любого П (одно ребро);

2. Если Т-ребро, инцидентное, то П является совершенным (ВЫХОД), иначене инцидентная Т-ребру. В этом случае нужно построить дерево цепей, выходящих из вершиныи чередующихся по цвету рёбер (С – Т – С…);

3. Если все цепи закончились Т-рёбрами, то совершенного П не существует (ВЫХОД), иначе существует цепь С – Т – С;

4. Перекрашиваем все рёбра этой цепи, т. е. ТС, СТ, при этом число Т-рёбер увеличивается на 1;

5. Взять полученное паросочетание в качестве текущего и вернуться к пункту 2.

Пример.

I способ.

Видно, что найдено совершенное паросочетание, т. к. из каждой вершины X выходит ровно по одному Т-ребру.

II способ.

Задача о назначениях.

Имеется n видов работы иn работников .

–польза от назначения на.

Необходимо распределить работу между работниками так, чтобы получить максимум пользы.

Алгоритм.

Будем приписывать метки и менять их:

–метка вершины ;

–метка вершины .

1. 

2. Построить двудольный граф, соединив рёбрами ;

3. Если существует совершенное паросочетание, то оно определяет максимальное назначение (ВЫХОД), иначе построить Венгерским алгоритмом дерево Т цепей, которое доказывает, что совершенного паросочетания нет;

4. Для каждой вершины вычислить;

5. ;

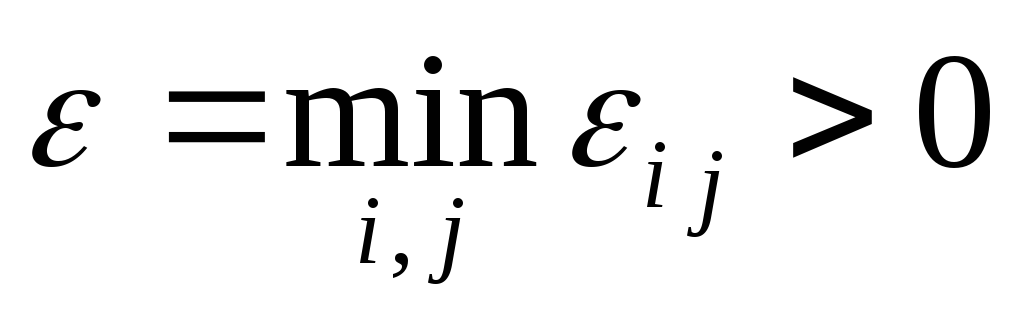6. Для каждой вершины изменить метки:

7. Вернуться к пункту 2.

Пример.

Смотри типовой расчет № 2.

Лекция № 10.

ЗАДАЧА О КРАТЧАЙШЕМ ПУТИ.

Дан ориентированный граф .– начальная,– конечная вершины.– длина дуги. Требуется найти путь изв, который обладает минимальной суммой весов входящих в него рёбер среди всех таких путей изв.

Алгоритм поиска минимального пути.

–временная метка вершины V (верхняя оценка длины минимального пути из в);

–постоянная метка вершины V (точное значение длины минимального пути из в).

Этап I – нахождение длины минимального пути из в, т. е.

V – текущая вершина.

1. 

2. 

3. Построить множество вершин, в которые ведут дуги изV;

4. Для каждой вершины обновить временную метку;

5. Найти вершину с минимальной временной меткой (если их несколько, то берём любую);

6. ;

7. Если , тои вернуться к пункту 3.

Этап II – построение пути.

Путь в виде списка L строим с конца.

1. 

2. Построить множество вершин, из которых идут дуги вV;

3. Найти вершину (если их несколько, то берём любую).

4. 

5. Если , то вернуться к пункту 2, иначе ВЫХОД.