Следствие.

Дерево и лес являются двудольными графами.

Следствие.

В простом планарном двудольном графе .

Если есть циклы, то они имеют длину и, т. к. каждая грань ограничена как минимум четырьмя рёбрами и все рёбра ограничивают не более двух гранейесли.

Если нет циклов, то т. к..

Следствие.

Граф не планарен.

Определение 6.

Графы называются подобными , если один из них может быть получен из другого в результате конечного числа введения или изъятия проходных вершин, т. е. вершин степени 2. В частности, любые два цикла являются подобными

Введение.

Изъятие.

Теорема 3 (критерий планарности Л. С. Поптрягина-Куратовского).

Граф планарен не имеет подграфов подобных графуи не имеет подграфов подобных графу.

(Доказательство теоремы очень сложное и не рассматривается).

Пример.

Рассмотрим граф Петерсена G.

Рассмотрим подграф .

Удалим проходные вершины .

не является планарным.

Замечание.

Графы иминимальные непланарные графы.

Лекция № 7.

РАСКРАСКА ГРАФА.

Определение 1.

Раскрасить граф – приписать его вершинам цвета 1,2,3… так, чтобы смежные вершины обязательно были раскрашены в разные цвета.

Минимальное число цветов, достаточное для раскраски графа G называется его хроматическим числом («хи»).

Утверждение 1.

Свойства хроматического числа:

1. 

2. Если граф содержит клику , то.

3. –цикл длины l, то

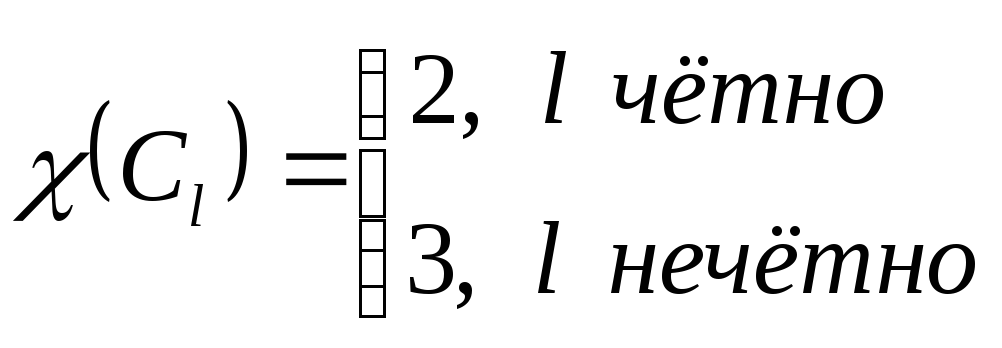
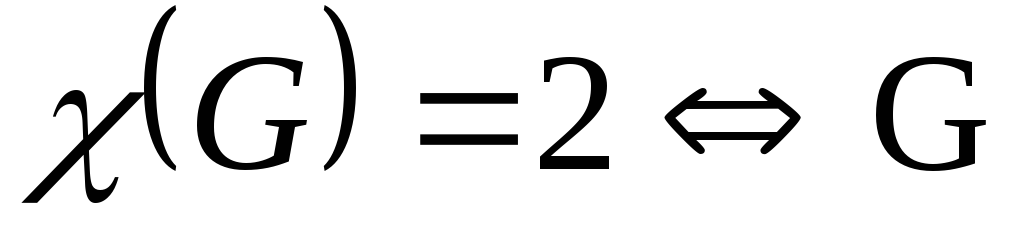4. –двудольный граф.

5. Если граф планарен, то (теорема о 4-х красках, Аппель и Хакен)

Теорема 1. «О пяти красках».

Если граф планарный, то его хроматическое число .

Докажем индукцией по числу вершин.

Если очевидно (базис индукции). Индуктивный переход. Пусть это верно для всех планарных графов, имеющихвершин. Рассмотрим граф сn вершинами.

По одному из следствий формулы Эйлера в графе существует вершина, степень которой .

А. Если степень вершины , то удалим вершину, получим граф, имеющийвершин. По индуктивному предположению его можно раскраситьцветами. При этом вершины, смежные св исходном графе окрашены не более, чем в 4 цвета, т. к. их всего. Тогда добавляеми окрашиваем её в пятый цвет.

Б. Если , то рассмотрим пять вершин, смежных с. Среди этих вершин есть, по крайней мере, 2е не смежные (например,и). Если бы таких вершин не было, то образовался бы граф, которого не может быть в силу планарности.

Отождествим вершины ,,Получим граф с меньшим числом вершин. Опять воспользуемся индуктивным предположением и раскрасим графцветов. Восстановим исходный граф, для всех вершин, кромеимы сохраним их окраску, а вершины,окрасим в пятый цвет. 

Пример.

Построена раскраска в 3 цвета .

Эвристический алгоритм:

1. Упорядочить вершины по невозрастанию степеней.

2. Найти минимально независимое множество, раскрасить вершины этого множества в один цвет.

3. Удалить окрашенные вершины со всеми инцидентными рёбрами. Получим подграф. Вернуться к пункту 1.

Замечание.

Эвристический алгоритм может привести к неоптимальной раскраске.

Лекция № 8.

ПРАВИЛЬНЫЙ ГРАФ.

Определение 1.

Граф называется однородным степени d, если .

Определение 2.

Пусть граф G является плоским. Двойственный графу G мульти граф

G G*

Следствие.

Определение 3.

Граф называется правильным, если он однородный, плоский и его G* однородный.

Утверждение.

Для правильного графа .

. Каждое ребро разделяет ровно 2 грани .

Утверждение.

Если G – правильный граф степени d, то .

Подставляем в формулу Эйлера



Найдём все правильные графы:

d	d*	n	m	f
1	2	2	1	1
2	n	n	n	2
3	3	4	6	4
3	4	8	12	6
4	3	6	12	8
3	5	20	30	15
5	3	15	30	20

тетраэдр

куб

октаэдр

додекаэдр

икосаэдр