Пример.

–все минимальные доминирующие множества.

Теорема 3.

Независимое множество является максимальным оно является доминирующим.



Пусть А – максимальное независимое множество. При соединении любой другой вершины нарушаем независимость, т. е. любая другая вершина смежная с вершиной из множества А множество является доминирующим.

Пусть А – доминирующее независимое множество…

Следствие.

Лекция № 6.

ИЗОМОРФНЫЕ, ПЛОСКИЕ И ПЛАНАРНЫЕ ГРАФЫ.

Определение 1.

Графы иназываются изоморфными, если существует биекция, сохраняющая отношения симметричности, т. е..

Определение 2.

Изображение графа называется плоским, если его рёбра пересекаются только в вершинах.

Определение 3.

Граф, для которого существует, изоморфное ему, плоское изображение называется планарным.

Пример.

плоский не плоский

Определение 4.

Пусть G – плоское изображение графа.

Его грань – это часть плоскости, для любых двух точек которой существует непрерывная кривая, соединяющая их и не пересекающая рёбра графа.

Пример.

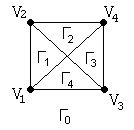
Замечание.

Любой граф имеет ровно одну бесконечную грань , конечная грань всегда ограничена циклом.

Теорема 1. (формула Эйлера для связных плоских графов)

Если n – число вершин, m – число рёбер, f – число граней и граф плоский и связный, то .

Рассмотрим остов Т графа G.

Далее будем прибавлять по одному ребру, достраивая остов до графа G число рёбер и граней увеличивается на единицу .

Замечание.

Для несвязных плоских графов эта теорема не верна, а верна следующая формула , где– число компонент связности.

Замечание.

Формула Эйлера верна также для плоских псевдо и мульти графов.

Пример.

Следствия из формулы Эйлера:

1. Простой связный планарный граф с вершинами и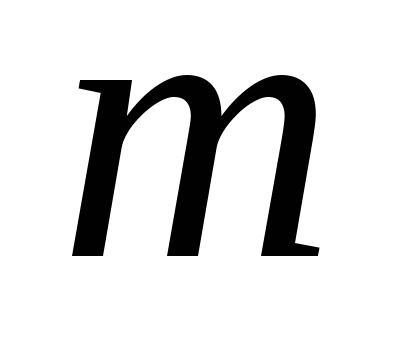рёбрами удовлетворяет неравенству

2. В любом планарном графе есть вершина, степень которой .

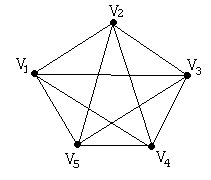
3. Граф не является планарным.



1.

А. Если есть цикл , т. к. любая грань ограничена как минимум 3-мя рёбрами и каждое ребро входит в границу не более чем двух граней.

Из формулы Эйлера:

Б. Если нет цикла, то граф является деревом.

Б1.

Б2.

.

2.

По теореме о сумме .

Если , топротиворечие свойству 1.

3.



Определение 5.

Граф называется двудольным, если его множество вершин может быть разбито на два подмножества:

X называется левой долей, а Y – правой.

Теорема 2.

Граф является двудольным все его простые циклы имеют чётную длину.



Рассмотрим двудольный граф и его простой цикл длины l .

Пусть , тогда реброприведёт вY, ребро приведёт вX и т. д.

должно быть чётно.

Пусть все простые циклы имеют чётную длину. Фиксируем . Назовём расстоянием между вершинами– длинаmin цепи, соединяющей и.

Р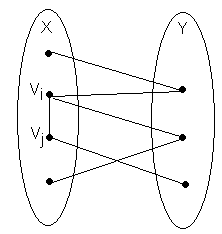азобьем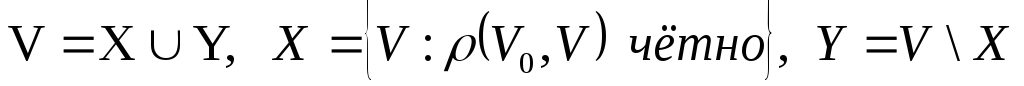. Покажем, что в этом случае рёбра соединяют вершины из разных долей.

Пусть простая цепьчётной длины, соединяющаяи, ипростая цепьчётной длины, соединяющаяи– цикл нечётной длины.

Аналогично, если мы допустим 