Лекция № 1.

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ.

Определение 1.

Граф обозначается , где – множество вершин графа, а– множество ребер, причем.

Определение 2.

Ребра бывают неориентированные , для которых порядок вершин не важен, и ориентированные– ориентированное ребро, или дуга. Стрелка от вершиныкпоказывает направление ориентации дуги.

Определение 3.

Вершины называются смежными, если существует ребро, которое их соединяет. Смежными называются ребра, имеющие общую вершину.

Определение 4.

Пусть , тогдаиназываются инцидентными.

Определение 5.

Если существуют несколько ребер, соединяющих две вершины, то такие ребра называются параллельными (кратными), причем кратность равна количеству ребер.

Определение 6.

Петлей называется ребро с совпадающими началом и концом.

Определение 7.

Граф называется простым, если он не содержит петель и кратных ребер.

Псевдограф – граф без кратных ребер.

Мультиграф – граф, содержащий петли и кратные ребра.

Определение 8.

Степенью вершины называется число ребер, инцидентных вершине. Петля в степени вершины учитывается дважды.

Теорема 1. (О сумме степеней вершин)

В любом графе, включая псевдограф и мультиграф, .

–число ребер, соединяющих и. Тогда. Каждое ребро в этой сумме содержится в двух слагаемыхи.

Следствие (лемма о рукопожатиях).

Число вершин нечетной степени четно.

Сумма степеней вершин чётной степени всегда чётно. А сумма степеней ВСЕХ вершин также должна быть чётной (по теореме о сумме степеней вершин). Следовательно, и сумма степеней вершин с нечётной степенью должна быть чётна, что возможно лишь в случае, когда чётно их число (сумма чётного числа нечётных слагаемых всегда чётна, а сумма нечётного числа нечётных слагаемых всегда нечётна).

Определение 9.

Маршрут – чередующаяся последовательность инцидентных друг другу вершин и ребер, начинающаяся и заканчивающаяся в вершине. Длина маршрута – число ребер в нем.

Определение 10.

Цикл – замкнутый маршрут, начинающийся и заканчивающийся в одной вершине.

Определение 11.

Цепь – маршрут без повторяющихся ребер.

Простая цепь – маршрут без повторяющихся вершин и ребер.

Пример.

–маршрут (не цепь!) длиной 3.

–цепь, но не простая.

–простой цикл, длины 3.

Определение 12.

Матрица смежности простого графа ,

, где

Свойства матрицы смежности:

1. Симметричность.

2. Элементы главной диагонали .

3. Число единиц в строке (столбце) равно.

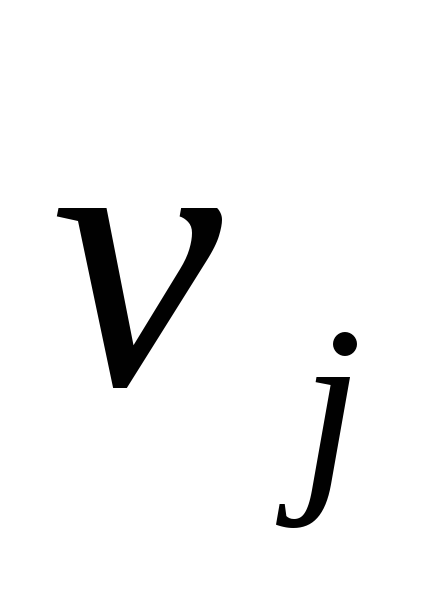4. Диагональный элемент равен. А произвольный элемент матрицыравен числу маршрутов длины, соединяющихи. Доказательство проводится индукцией по показателю степени.

Определение 13.

Матрица инциденций простого графа

Свойства матрицы инциденций:

1. В каждом столбце ровно 2 единицы.

2. Число единиц в строке равно степени вершины.

3. Каждый минор равен либо 0, либо +1, либо -1.

Определение 14.

Подграф графа :

Определение 15.

Граф называется связным, если любые две вершины имогут быть соединены маршрутом. Максимальный связный подграф называется компонентой связности. Таким образом, связный граф имеет одну компоненту.

Граф	Орграф
Ребро	Дуга
Степень вершины	Полустепень исхода Полустепень захода
Маршрут	Путь
Цикл	Контур
Матрица смежности
Матрица инцидентности