Св-ва двойного интеграла

Пусть D – квадрируемое мн-во

1)=S; S – площадь D

Док-во f(x,y)=1 на D. Рассм.разбиениемн-ва D:=Т.к.,=>=S =>Q_i=>==>=S



2)Пусть ф-ции f(x,y) и g(x,y) интегр. На мн-ве D. Тогда ф-ция [f(x,y)+g(x,y)] интегр. На мн-ве D и=+

3)Пусть f интегр на мн-ве D. Тогда дляА-const ф-ция {Af(x,y)} интегр. на D и=

4)Пусть f интегр. на D и D=D₁D₂ D₁и D₂квадрир. мн-ва, т.ч.Тогда=+

5)Пусть ф-ции f(x,y) и g(x,y) интегр. на D и f(x,y)g(x,y)(x,y)D Тогда

6)Пусть f(x,y) интегр на D, тогда ф-ция |f(x,y)| интегр на D и ||

Док-ва 2)-6) совпадают с док-ми соотв. св-в для определенного интеграла



Билет №26 Теорема о среднем для двойного интеграла

Теорема(о среднем): Пусть D – связный компакт и ф-ция f(x,y) непрерывна на D, тогдаМD, т.ч.=f(M)S, S – площадь D.

Док-во:D – компакт и f непрерывна на D =>М₁,М₂D: f(М₁)=, f(М₂)==> f(М₁)f(x,y)f(М₂)(x,y)D По св-ву 5)(билет 25):

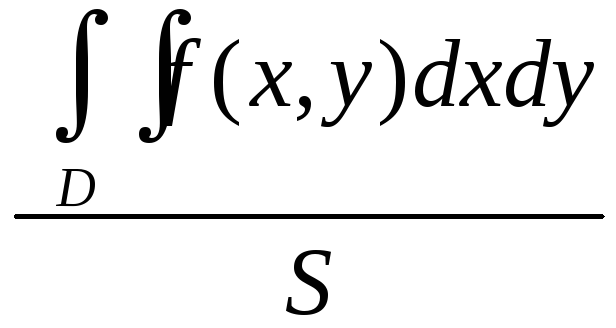
По свойствам 1),3) (билет 25): f(М₁)Sf(М₂)S=> f(М₁)f(М₂)

Обознач. => f(М₁)f(М₁)

Т.к. D – связное мн-во и f непрерывна на D => МD: f(М)==>

f(M)= => f(M)S=, МD

Билет №27.Сведение двойного интеграла к повторному.

Пусть D=

Множество D– криволинейная трапеция относительно множестваOX.

Теорема: Если f(x,y) непрерывна на множествеD, заданном формулой (1).

Тогда – повторный интеграл.

Доказательство: 1) 2)f(x,y) непрерывна наD=>f(x,y) непрерывна на поyна [] для=.

3) Формулу (2) докажем в частном случае, когда D-прямоугольник со сторонами || - осям

координат.

D=[a,b]x[c,d] наnравных частей точками:a=<< … <<=b,c=<< … <<= =d. Обозначим,k=1…n,l=1…n. Тогда τ=– разбиение множества =>Так какповторный интеграл => I== {по свойству аддитивности для определенного интеграла} == {аддитивность} == ={линейность} =.f(x,y) непрерывна наD=>f(x,y) непрерывна поyна[],l=1,n. При=> по теореме о среднем для определенного интеграла:где, =>={так какf(x,y) непрерывна наD=> функцияf(x,на=> по теореме о среднем для определенного интеграла:,} ==,=>=Имеем:С другой стороны==>=>

Рассмотрим множество G=(3), где,- непрерывны на [c,d] =>G– криволинейная трапеция относительноOY:

Теорема: Пусть f(x,y) непрерывна на множествеG, заданном формулой (3), где,- непрерывны на [c,d]. Тогда:.

Билет №28.Замена переменных в двойном интеграле.

Пусть Пусть пара функций, (), отображаетна плоскости переменныхx,y.

Предположим, что выполнены условия:

1) функции непрерывно-дифференцируемы на.

2) отображение взаимно-однозначное.

3) Определитель 0,()называется якобианом отображенияОтображениевзаимно-однозначные, если:

1)

2)

Если - ограниченное множество с кусочно-гладкой границейи отображениеудовлетворяет условиям 1)-3), тос кусочно-гладкой границейграница

Теорема:

Если функция f(x,y) непрерывна наи выполнены условия 1-3, тогда;

Док-во:

1. Т.к. f(x,y) непрерывна на=>.

2. Т.к. f(x,y) непр-на на, ф-ии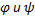непр-но дифф-мы на, то функциянепр-на на=>

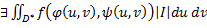
Формулу (1) докажем для частного случая линейного отображ.:

,a,b,c,d– числа.

Введем на площади прямоугольную cетку с шагомh.

Эта сетка в случ. лин. отобр. переходит в прямоугольную сетку на пл-ти x,y.

Рассм. такие квадраты на пл-ти u,v, которые имеют ненулевое пересечение с. Пересечение этих квадратов собразует разбиениемн-ва.

Обозн. – образпри отображении (*) =>– разбиение мн-ваD.

Т.к. вып. условия 1-3 и все мн-ва - квадрируемые (т.к.ограниченное мн-во с кусочно-гладкой границей), то– тоже квадрируемые мн-ва. Обозн.– площадь,– площадь.

Выбираем точку; обозначим черезобразпри отображении (*)=>.

Составим интегральную сумму: .

Выберем в разбиении tвсе такие мн-ва, которые не пересекаются с Г и.

Пусть .

Ан-но , т.ч.не пересекаются с.

Т.к. граница переходит в границу Г (в силу усл. 1-3), то<=>=>

, где- сумма по;

- сумма по, т.ч..

Рассм. . Если=>- образ целого квадрата.

- квадрат, построенный на векторах (h,0),(0,h).

Вектора (h,0),(0,h) переходят в вектора

– параллелограмм, построенный на векторах.

.

Якобиан отображения:

=>=>

.

Обозн. =>.

Имеем:

. Интегральная сумма дляF, соответствующая разбиению:.

Пусть – параметр разбиенияt,- параметр разбиения.

(т.к.). Т.к.=>

. Т.к.=>.

Докажем что .

f(x,y) непрерывна на,– компакт =>fогран. на.

, т.к. Г – кусочно-гладкая кривая =>S(Г)=0 =>.

Аналогично =>.

.

=>.

Билет №29.Тройной интеграл и его свойства. Сведение тройного интеграла к повторному.

Мн-во в R₃, являющееся объединением конечного числа прямоугольных параллелепипедов, ребра которых параллельны осям координат называется элементарным телом.

Поверхность Sназ-ся поверхностью объема (меры) нуль, еслиэлементарное телот.ч..

Например, гладкая поверхность имеет объем нуль, кусочно-гладкая поверхность имеет объем нуль.

Пусть -ограниченное мн-во вR₃. Мн-вокубируемо <=> мера его границы равна нулю.

Док-во аналогично док-ву критерия квадрируемости мн-ва.

Пусть–ограниченное мн-во вR₃с кусочно-гладкой границей. Разбиваемнаnчастейс помощью кусочно-гладких поверхностей так, чтобы выполнялись св-ва:

1);2) ,ij;

Мн-во t={}, т.ч. выполнены условия 1, 2 называется разбиением.

Обозн. – объем. Обозн. d_i=diam . Пусть=maxd_i– параметр разбиения.

Выбираем точку Q_i. Пустьf(x,y,z) опред. на мн-ве.Составим интегральную сумму:

Если lim(), не зависящий от разбиенияtи выбора точекQ_i, то этот предел называется тройным интегралом от функцииfпо мн-ву. Обознач.

Функция f(x,y,z) наз-ся интегрируемой на, если.

Необходимое условие интегрируемости, достаточное условие интегрируемости, критерий интегрируемости, критерий интегрируемости формулируются и док-ся также как и для двойного и определенного интеграла. Например:

Дост. условие интегрируемости: если fнепрерывна на, тоfинтегрируема на(где- кубируемое мн-во).

Св-ва тройного интеграла:

1), гдеV– объем. Док-во:

Рассм. и выбираем=>=>lim()=V,Vне зависит отtи т.Q_i =>

2) Пусть функции f,gинтегрируемы на. Тогда {f+g} интегрируема наи

3) Пусть fинтегрируема на. Тогда дляфункция {Af} интегрируема наи.

4) Пусть fинтегрируема наигде. Тогда.

5) Пусть fиgинтегрируемыиf(x,y,z)≤g(x,y,z). Тогда.

6) Пусть fинтегрируема на, тогда |f|интегрир. наи.

7) Теорема о среднем:

Пусть – связный компакт вR₃ и функцияf(x,y,z) непр-на на. Тогда,V– объем

Св-ва 2-6 доказываются как для определенного интеграла; 7 док-ся как для двойного интеграла.

Сведение тройного интеграла к повторному.

Рассм. мн-во G={} (1), где,Dквадрир. мн-во

функциинепрерывны на. Мн-воG, заданное (1) называется цилиндроидом от-ноxy.

Теорема:

Пусть f(x,y,z) непр-на наG, гденепр. на. Тогда(2). Интеграл в правой части (2) наз-ся повторным.

Док-во: в частном случае когда G– параллелепипед с ребрами, ||-ми осям координат, проводится аналогично для соответствующей формулы для двойного интеграла.

Аналогично вводятся цилиндры отн-но плоскостей xzиyzи формулируется теорема о сведении тройного интеграла к соответствующим повторным.

Билет № 30. Замена переменной в тройном интеграле

Пусть - ограниченное мн-во в пространстве переменныхu,v,wс кусочно-гладкой границей.

Пусть система функций: (*)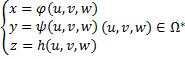

отображает на мн-вов пространстве переменныхx,y,z. Предполагаем, что выполнены условия:

1. ф-ии непрерывно дифф-мы на,

2. отображение (*) – взаимооднозначное ,

3. определитель I=. Определитель наз-ся якобианом отображения (*)

Если отображение (*) удовлетворяет условиям 1-3, то ограниченное мн-во с кусочно-гладкой границейотображается на ограниченное мн-вос кусочно-гладкой границей, причемотображается на

Теорема: Пусть ф-ия f(x,y,z) непр-на наи выполнены условия 1-3 для отображения (*). Тогда:.

Док-во аналогично.

Сферические координаты

Θ– угол между осьюOZи(Θ– сферический угол).

φ – угол от основания OXдо(φ – полярный угол)

(r,Θ, φ) – сферические координаты.

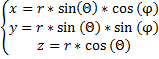
I= = = r²*sin (Θ)→|I|= r²*sin (Θ)

(т.к. 0≤ Θ≤π→sin(Θ)≥0)

Формула замены переменных в случае сферических координат имеет вид:

Цилиндрические координаты

M’ – прокцияMна плоскостьOxy

(r,φ) – полярные координаты т.M.

=>(r,φ,z) – цилиндрические координаты т.M

I=→r≥0→|I|=r

Формула замены переменной в случае цилиндрических координат имеет вид:

Билет №31(Криволинейный интеграл 1-го рода и его св-ва)

Пусть Г – ограниченная кусочно-гладкая кривая без точек самопересечения.

Разбиваем Г на nчастей точками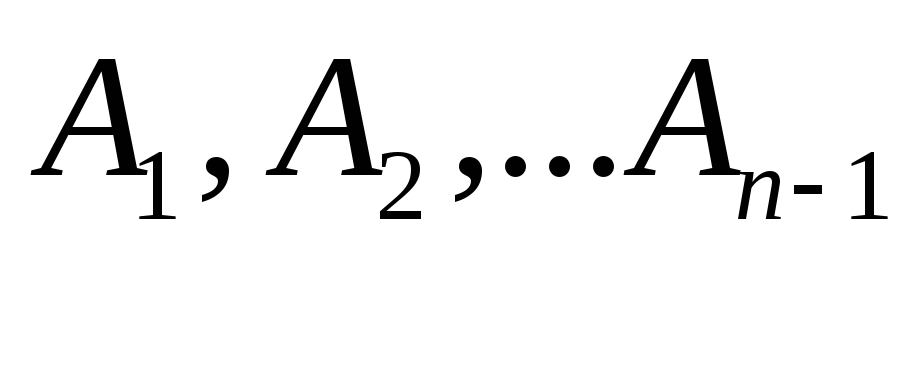. Обозначим. Обозначим через- длинна дуги..

Мн-ва точек T=называем разбиением Г,- параметр разбиения Т. Выбираем произвольные точки. Пусть ф-яопределена на Г. Составляем интегральную сумму: .

ОпрЕсли, не зависящий от разбиенияTи выбора точек, то этот предел наз-ся криволи-ым интегралом 1-го рода от ф-цииfпо кривой Г и обозна-ся. Ф-циюfназывают интегрируемой по Г, если.

Св-ва криволинейного интнграла 1-го рода

1) L– длинна кривой Г.

Док-во: рассматриваем разбиениеT=кривой Г и выбираемточкигдена Г

2) Пусть интегрируема по Гдля

3) Пусть ф-ции f(x,y,z) иg(x,y,z) интегрируемы по Г. Тогда(св-во линейности).

4) Пусть f(x,y,z) интегрируема по кривой АВ и точка САВ. Тогда(св-во аддитивности).

5) Пусть интегрируема по кривой Г. Тогда ф-яинтегрируема по Г и.

6) Пусть иинтегрируема по Г ина Г. Тогда. Док-во св-в 2-6 аналогично док-вам св-в для определенного интеграла.

Пусть кривая Г задана параметрически урав-ми

где непрерывно дифференцируемы на. Пусть ф-цияопределена на Г. Говорят, что ф-янепрерывна на Г, еслинепрерывна на.

Теорема (О среднем): пустьнепрерывна на Г. Тогдатакая, что,- длинна Г. Док-во теоремы аналогично дов-ву о среднем для определеного интеграла.

Замечание:криволинейный интеграл 1-го рода не зависит от направления обхода (величина) на кривой. Рассмотрим интегральную сумму, т.к ине зависят от направления обхода кривойинтегральная сумма не зависит от направления обхода криволинейный интеграл 1-го рода не зависит от направления обхода на Г.

Билет №32. Существование криволинейного интеграла 1 рода и его вычисление.

Пусть кривая Г задана параметрически :

Кривая Г называется гладкой, если функции непрерывно дифференцируемы на [a;b] и

Теорема.

Пусть Г-гладкая кривая заданная уравнениями (1) и непрерывна на Г. Тогда:

Доказательство.

Т.к функция fнепрерывна на Г, функциинепрерывно дифференцируемы на [a;b] то сложная функциянепрерывна на [a;b] =>

Рассмотрим Разбиение кривойT

Пусть- параметр разбиения Т. Выбираемточки

Составляем интегральную сумму:

=

Для точки,) причем;

=> разбиение

Для ,)

Т.к. непрерывно дифференцируемы на=> функциянепрерывна на=> по теореме о среднем для определенного интеграла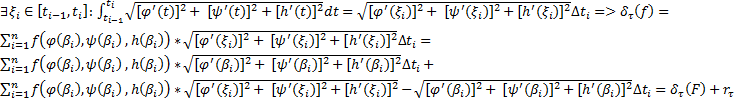

Т.к F(t)непрерывна на=>- параметр разбиения

Докажем что ФиксирФункциянепрерывна на=> Она ограничена нат.е.

Т.к. непрерывно дифференцируемы на=>непрерывны на=> для

Т.к можно счиать что

Имеем

Т.к,

И =>

;=>

=если=>=>

=>

Докажем что если

,

Функция непрерывна на=> Эта функция достигаетminназначенияm

Т.к. на=>m>0 =>т.е.

=> =>

Т.о. Т.к.m=>

Т.е.