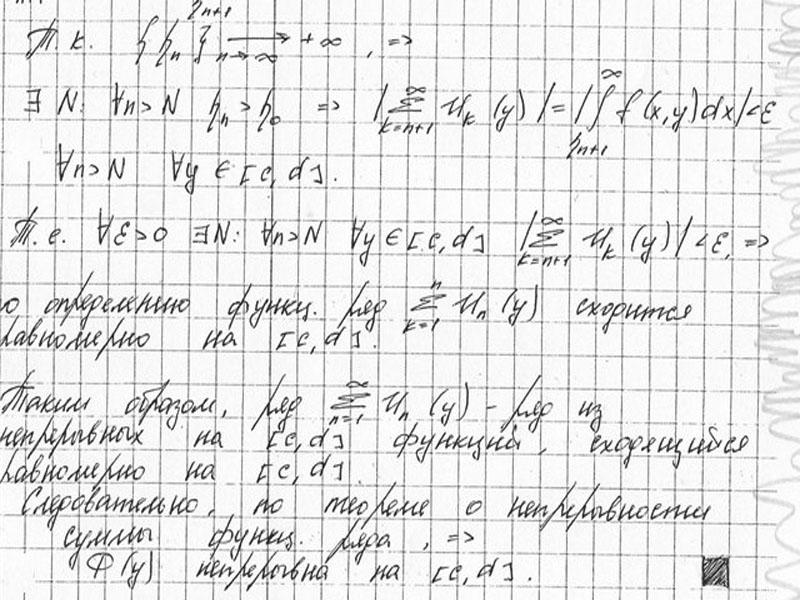- •8. Почленное дифференцирование функционального ряда
- •17. Равномерная сходимость тригонометрического ряда Фурье (без док-ва).
- •20. Несобственные интегралы, зависящие от параметра. Равномерная сходимость. Признак Вейерштрасса.
- •21. Непрерывность несобственного интеграла, зависящего от параметра.
- •22. Дифференцирование несобственного интеграла, зависящего от параметра.
- •23.Кривая площади нуль. Примеры (теорема).
- •24. Критерий квадрируемости множества.
- •Св-ва двойного интеграла
- •3 В .3.Криволинейный интеграл 2ого рода и его свойства.
- •37. Поверхностный интеграл 1 рода и его свойства.
- •38. Существование поверхностного интеграла 1 рода и его вычисление.
- •46. Дивергенция. Геометрическое определение дивергенции.
- •47. Поток векторного поля через поверхность. Векторная формулировка теоремы Остроградского-Гаусса.
- •48. Ротор. Циркуляция. Теорема Стокса.
- •49. Условия независимости криволинейного интеграла от пути интегрирования.
20. Несобственные интегралы, зависящие от параметра. Равномерная сходимость. Признак Вейерштрасса.
Рассм. интеграл (1) ![]() ,yєY,a<b<+
,yєY,a<b<+![]() ,
где для
,
где для![]() фиксир.
фиксир.![]()
интеграл (1) несобств.
Тогда интеграл (1) наз. несобств. инт-лом,
зависящим от параметра, ![]() -
параметр. Далее рассм. несобств. инт-л,
зависящ от параметра вида (2)
-
параметр. Далее рассм. несобств. инт-л,
зависящ от параметра вида (2)![]() ,
зависящий от параметраyєYНесобств. инт-лы (1), гдеb– конеч. число, рассм-ся анал-но.
,
зависящий от параметраyєYНесобств. инт-лы (1), гдеb– конеч. число, рассм-ся анал-но.
Предположим, что для ![]() фиксир
фиксир![]() ф-я
ф-я![]() интегрируема на
интегрируема на![]() конечном промежутке
конечном промежутке![]()
Опр. Инт-л (2) сх-ся на мн-ве У, если для
![]() фиксир.
фиксир.![]() интеграл
интеграл![]() сх-ся, т.е. для
сх-ся, т.е. для
![]() фиксир.
фиксир.![]()
![]() (обозн)
(обозн)
Другими словами ![]()
![]()
![]()
![]()
![]()
![]()
Равномерная сходимость несобственных интегралов, зависящих от параметра.
Опр. Инт-л (2) сх-ся равномерно на мн-ве
У, если ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Замечание. Если инт-л (2) сх-ся равномерно на У, то он сх-ся на У. Обратное неверно.
Т. (Критерий Коши равномер. сх-сти)
Инт-л (2) сх-ся равном на S![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Для доказательства критерия Коши необх. рассм. единство функций
Ф (![]() и док-ся Крит.Коши равном сх-ти сем-ва
ф-ий,из кот след.крит.Коши равном сх-ти
несобств.инт-лов.
и док-ся Крит.Коши равном сх-ти сем-ва
ф-ий,из кот след.крит.Коши равном сх-ти
несобств.инт-лов.
Теорема.(Критерий Коши для ФП)
Функциональная последовательность
![]() сходится равномерно на Е
сходится равномерно на Е![]()
Доказательство
=>
{![]() Сходится равномерно на Е =
Сходится равномерно на Е =![]()
![]() функция
функция![]() ,определена на Е, т.ч.
,определена на Е, т.ч.![]() на Е
Фиксируем
на Е
Фиксируем![]()
Для ![]()
![]()
=> ![]()
![]() =
=![]()
![]()
<=
![]() для
для![]() фиксированного
фиксированного![]() для числовой последовательности{
для числовой последовательности{![]() выполнен Критерий Коши => для
выполнен Критерий Коши => для![]() фиксированного
фиксированного![]() числовая последовательность{
числовая последовательность{![]() сходится к некоторому числу =>
функциональная последовательность{
сходится к некоторому числу =>
функциональная последовательность{![]() сходится к некоторой функции
сходится к некоторой функции ![]() на множестве Е. Докажем что функц.
Последовательность
на множестве Е. Докажем что функц.
Последовательность![]() на Е
на Е
Имеем по условию: ![]()
![]() (1*)
(1*)
Т.к ![]()
Для ![]()
![]() Переходим в неравенство(1*)к
Переходим в неравенство(1*)к![]() =>
=>![]()
![]()
![]() => ФП
=> ФП![]() на Е.
на Е.
Док-во крит Коши для ед-ва ф-й полностью анал-но док-ву крит Коши для ф-й послед-сти.
Т. (признак Вейерштрасса)
Пусть ![]() неотриц ф-я
неотриц ф-я![]() т.ч.
т.ч.
![]() сх-ся и
сх-ся и![]()
![]()
![]() ,
,
![]() є
є![]() , +
, +![]() Тогда
Тогда![]() сх-ся равномерно на У.
сх-ся равномерно на У.
Д.1) Д-м, что![]() сх-ся на У.
сх-ся на У.
т.к. ![]()
![]()
![]()
![]()
![]() є
є![]() , +
, +![]() и
и
![]() сх-ся, то призн сравнения для
сх-ся, то призн сравнения для![]() фикс
фикс![]() сх-ся инт-л
сх-ся инт-л
![]()
![]() сх-ся
(абсол)
сх-ся
(абсол)
для ![]() У
У![]()
(3) ![]()
![]()
Т.к. ф-и ![]() (для фикс у) и
(для фикс у) и![]() инт-мы на
инт-мы на![]() [a,η]⊂[a,+
[a,η]⊂[a,+![]() ],
то
],
то![]() η
η![]() инт-лы
инт-лы![]() ,
,![]() ,
,![]() сх-ся (для
сх-ся (для![]() фикс.y
фикс.y![]() Y)
и справедливы нер-ва
Y)
и справедливы нер-ва![]()
![]()
![]() y
y![]() Y(4).
2)Д-м,что
Y(4).
2)Д-м,что![]() сх-ся равномерно неY.
имеем
сх-ся равномерно неY.
имеем![]() сх-ся
равномерно наY. Имеем
сх-ся
равномерно наY. Имеем![]() сх-ся
сх-ся![]() η0
η0![]() η> η0
η> η0![]() <
<![]() .
Из (4)получ., что
.
Из (4)получ., что![]() y
y![]() Y
Y![]() <
<![]()
![]() η> η0
η> η0![]() η0
η0![]() η> η0
η> η0![]() y
y![]() Y
Y![]()
![]()
![]() сх-ся равномерно наY.
сх-ся равномерно наY.
21. Непрерывность несобственного интеграла, зависящего от параметра.
Т.Пусть![]() непрерывна (по совокупности переменных)
на
непрерывна (по совокупности переменных)
на![]() х
х![]() (декартово произведение) и интеграл
(декартово произведение) и интеграл![]() сходится равномерно на
сходится равномерно на![]() , тогда ф-ция
, тогда ф-ция
Ф(у)=![]() непрерывна на
непрерывна на![]()
Д .Рассмотрим посл-сть точек
.Рассмотрим посл-сть точек![]() ,
такую что
,
такую что![]()
![]()
![]()
Рассмотрим функц. ряд ![]()
![]()
![]()
![]()
Докажем, что ряд (5) сходится на ![]() .
.
Рассмотрим частную сумму ряда: ![]()
Т.к. ![]() сходится равномерно на
сходится равномерно на![]() ,
,![]()
![]()
Последовательность ![]()
![]()

![]()
![]()
ряд ![]()
![]() сумма
сумма![]() Докажем, что ф-ция
Докажем, что ф-ция![]() непрерывна на
непрерывна на![]()
![]() nф-ияUn(y)=
nф-ияUn(y)=![]() - собств. инт-л , зависящий от парам-ра.
- собств. инт-л , зависящий от парам-ра.
Т.к. f(x,y)
непрер. на мн-ве![]() х
х![]() f(x,y)
неперер.на
f(x,y)
неперер.на![]() х
х![]()
![]() n
n![]() по теор. о непрер-ти собств. инт-ла,
зависящего от параметра, все ф-ииUn(y)
непрер. на [c,d]Докажем,
что
по теор. о непрер-ти собств. инт-ла,
зависящего от параметра, все ф-ииUn(y)
непрер. на [c,d]Докажем,
что![]() сх-ся
равномерно на [c,d].
сх-ся
равномерно на [c,d].
Т.к ![]() сх-ся равномерно на [c,d]
сх-ся равномерно на [c,d]![]() >0
>0![]() :
:![]() η>η0
η>η0![]() [c,d]
|
[c,d]
|![]() <
<![]()
Т.к. функц.ряд ![]() сх-ся
на [c,d]
сх-ся
на [c,d]![]() сх-ся
сх-ся![]() на [c,d]
на [c,d]![]() ,
причем
,
причем![]() =
=![]() .
.
Т.к