
- •8. Почленное дифференцирование функционального ряда
- •17. Равномерная сходимость тригонометрического ряда Фурье (без док-ва).
- •20. Несобственные интегралы, зависящие от параметра. Равномерная сходимость. Признак Вейерштрасса.
- •21. Непрерывность несобственного интеграла, зависящего от параметра.
- •22. Дифференцирование несобственного интеграла, зависящего от параметра.
- •23.Кривая площади нуль. Примеры (теорема).
- •24. Критерий квадрируемости множества.
- •Св-ва двойного интеграла
- •3 В .3.Криволинейный интеграл 2ого рода и его свойства.
- •37. Поверхностный интеграл 1 рода и его свойства.
- •38. Существование поверхностного интеграла 1 рода и его вычисление.
- •46. Дивергенция. Геометрическое определение дивергенции.
- •47. Поток векторного поля через поверхность. Векторная формулировка теоремы Остроградского-Гаусса.
- •48. Ротор. Циркуляция. Теорема Стокса.
- •49. Условия независимости криволинейного интеграла от пути интегрирования.
Билет 1. Функциональная последовательность (ФП). Область сходимости. Примеры.
Определение 1.
Если каждому натуральному числу nставится в соответствие по некоторому
закону функция![]() , определенная на множестве
, определенная на множестве![]() ,
то говорят, что на множестве Х задана
функциональная последовательность
,
то говорят, что на множестве Х задана
функциональная последовательность![]()
Множество Х называется областью
определения последовательности ![]()
Пример.
![]()
Область определения последовательности
![]() .
Пусть
.
Пусть![]()
Определение2.
Функциональная последовательность ![]() сходится в точке
сходится в точке![]() , если числовая последовательность
, если числовая последовательность![]() сходится.
сходится.
Множество всех точек ![]() , в которых функциональная последовательность
, в которых функциональная последовательность![]() сходится, называется областью сходимости
функциональной последовательности.
сходится, называется областью сходимости
функциональной последовательности.
Пример.
![]()
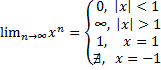 Область сходимости последовательности
Область сходимости последовательности![]() .
.
Пусть D– область сходимости
последовательности![]() .//обозначение
предельного значения//
.//обозначение
предельного значения//
Совокупность всех предельных значений
![]() являейтся функцией, определенной наD. Эта функция
являейтся функцией, определенной наD. Эта функция![]() называется предельной функцией
последовательности
называется предельной функцией
последовательности![]() .
.
Пример.
![]()
Замечание.
Поточечная сходимость ФП на множестве Dне гарантирует сохранение свойств членов последовательности (например свойства непрерывности, интегрируемости и т.д.)
Пример
![]()
![]() - область сходимости
- область сходимости![]() непрерывна наD
непрерывна наD
Предельная функция ![]() Функция
Функция![]() не является непрерывной наDт.к. имеет разрыв в точке х=1.
не является непрерывной наDт.к. имеет разрыв в точке х=1.
Билет 2. Функциональный ряд (ФР). Область сходимости. Абсолютная сходимость ФР.
Пусть дана функциональная последовательность
![]() Определенная на множествеX.
Определенная на множествеX.
Определение1
Формально написанную сумму
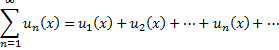 Будем называть функциональным рядом.
Будем называть функциональным рядом.
Множество Х называется областью определения ряда.
Сумма nпервых членов ряда![]() называетсяn– ной частичной
суммой ряда.
называетсяn– ной частичной
суммой ряда.
Заметим что ![]() является ФП, определенной на Х.
является ФП, определенной на Х.
Пусть точка ![]()
Определение 2.1
Функциональный ряд ![]() сходится в т.
сходится в т.![]() если числовой ряд
если числовой ряд![]() сходится.
сходится.
Множество Dточек![]() в которых ФР сходится, называется
областью сходимости ряда.
в которых ФР сходится, называется
областью сходимости ряда.
Определение2.2
Функциональный ряд ![]() сходится на множествеD,
если ФП
сходится на множествеD,
если ФП![]() его частичной суммы сходится наD.
его частичной суммы сходится наD.
Если ФР сходится на D, то его сумма есть функцияS(x)Определенная наD.
Очевидно S(x)
Есть предельная функция последовательности![]() частичных сумм ряда.
частичных сумм ряда.
Замечание
Поточечная сходимость ряда на множестве Dне гарантирует сохранение свойств членов ряда для суммы раяда (напремер свойство непрерывности)
Определение 3.
ФР ![]() сходится абсолютно на множествеD, если ФР
сходится абсолютно на множествеD, если ФР![]() Сходится на множестве
Сходится на множестве![]()
Утверждение 1.
Если ФР ![]() сходится абсолютно на множестве
сходится абсолютно на множестве![]() то он сходится на
то он сходится на![]()
Доказательство.
Ряд ![]() сходится абсолютно на
сходится абсолютно на![]() =>
ряд
=>
ряд![]() Сходится на
Сходится на![]() =>
=>![]() числовой ряд
числовой ряд![]()
Сходится => числовой ряд ![]() сходиться абсолютно => числовой ряд
сходиться абсолютно => числовой ряд![]() сходится (в обычном смысле).
сходится (в обычном смысле).
Т.к ![]() - любая точка из
- любая точка из![]() ФР
ФР![]() сходится на множестве
сходится на множестве![]()
![]()
Билет 3. Равномерная сходимость ФР, ФП. Критерий Коши (для ФП).
Дана ФП ![]() определенная на множестве Х.
определенная на множестве Х.
Определение.
Последовательность ![]() сходится равномерно на множестве Е⊂
Х, если
сходится равномерно на множестве Е⊂
Х, если![]()
![]()
![]()
Определение.
Последовательность ![]() сходится равномерно на Е, если
сходится равномерно на Е, если![]() функция
функция![]() ,
такая что
,
такая что![]() сходится равномерно к
сходится равномерно к![]() ,
на множестве Е
,
на множестве Е
![]() на Е
на Е
Определение 1.
Функциональный ряд ![]() сходится равномерно к функцииS(x)
на множестве
сходится равномерно к функцииS(x)
на множестве![]() Если последовательность частичных сумм
Если последовательность частичных сумм![]() сходится равномерно к функции
сходится равномерно к функции![]() на множестве Е.
на множестве Е.
Предположим что последовательность
![]() ,….,
,….,![]() сходится на множестве
сходится на множестве![]() к функции
к функции![]()
Теорема.(Критерий Коши для ФП)
Функциональная последовательность
![]() сходится равномерно на Е
сходится равномерно на Е![]()
Доказательство
=>
{![]() Сходится равномерно на Е =
Сходится равномерно на Е =![]()
![]() функция
функция![]() ,определена на Е, т.ч.
,определена на Е, т.ч.![]() на Е
Фиксируем
на Е
Фиксируем![]()
Для ![]()
![]()
=> ![]()
![]() =
=![]()
![]()
<=
![]() для
для![]() фиксированного
фиксированного![]() для числовой последовательности{
для числовой последовательности{![]() выполнен Критерий Коши => для
выполнен Критерий Коши => для![]() фиксированного
фиксированного![]() числовая последовательность{
числовая последовательность{![]() сходится к некоторому числу =>
функциональная последовательность{
сходится к некоторому числу =>
функциональная последовательность{![]() сходится к некоторой функции
сходится к некоторой функции ![]() на множестве Е. Докажем что функц.
Последовательность
на множестве Е. Докажем что функц.
Последовательность![]() на Е
на Е
Имеем по условию: ![]()
![]() (1*)
(1*)
Т.к ![]()
Для ![]()
![]() Переходим в неравенство(1*)к
Переходим в неравенство(1*)к![]() =>
=>![]()
![]()
![]() => ФП
=> ФП![]() на Е
на Е![]()
Билет 4. Равномерная сходимость ФР. Критерий Коши (для ФР). Необходимое условие равномерной сходимости ряда.
Пусть ФР ![]() определена на Х;
определена на Х;![]() –n-ая частичная сумма
ряда
–n-ая частичная сумма
ряда
Определение 1.
Функциональный ряд ![]() сходится равномерно к функцииS(x)
на множестве
сходится равномерно к функцииS(x)
на множестве![]() Если последовательность частичных сумм
Если последовательность частичных сумм![]() сходится равномерно к функции
сходится равномерно к функции![]() на множестве Е.
на множестве Е.
Теорема (Критерий Коши для ФР).
ФР ![]() сходится равномерно на Е
сходится равномерно на Е![]()
Доказательство.
ФР сходится равномерно на Е ФП частичных сумм![]() сходится равномерно на Е
сходится равномерно на Е
![]()
![]() Таким образом
Таким образом
![]()
![]()
Теорема(необходимое условие сходимости ряда)
Если ФР ![]() сходится равномерно на Е, тогда ФП
сходится равномерно на Е, тогда ФП![]() на Е
на Е
Доказательство.
ФР ![]() сходится равномерно на Е => (По Критерию
Коши)
сходится равномерно на Е => (По Критерию
Коши)![]() .
В частности приp=1 имеем
.
В частности приp=1 имеем![]() => ФП
=> ФП![]() на Е
на Е![]()
Билет 5. Признак Вейерштрасса равномерной сходимости ФР.
Теорема (Признак Вейерштрасса).
Пусть дан ФР на множестве Еи пусть
существует сходящийся числовой ряд ![]() такой что
такой что![]()
![]() ,n=1,2…. Тогда ФР сходится
равномерно и абсолютно на множестве Е.
В этом случае числовой ряд называется
мажорирующим рядом для ФР
,n=1,2…. Тогда ФР сходится
равномерно и абсолютно на множестве Е.
В этом случае числовой ряд называется
мажорирующим рядом для ФР![]() .
.
Доказательство.
1) Докажем , что ФР ![]() сходится абсолютно на Е
сходится абсолютно на Е
Имеем любой фиксированный ![]() :
:![]() n=1,2…. => для любого
фиксированного
n=1,2…. => для любого
фиксированного![]() числовой ряд
числовой ряд![]() сходится по признаку сравнения т.к.
сходится по признаку сравнения т.к.![]() сходится => ФР
сходится => ФР![]() сходится на множестве Е =>
сходится на множестве Е =>
ФР ![]() сходится абсолютно на множестве Е.
сходится абсолютно на множестве Е.
Кроме того, ФР ![]() Сходится равномерно к функции
Сходится равномерно к функции![]() на множестве Е.
на множестве Е.
2) Докажем что ФР ![]() сходится равномерно к функцииS(x)
на множествеE,
сходится равномерно к функцииS(x)
на множествеE,
Обозначим ![]() ,
,
![]() ,
,![]() Для
Для![]()
![]() .
Числовой ряд
.
Числовой ряд![]() сходится =>
сходится =>![]() =>
=>![]()
![]() =>
=> ![]()
![]() => ФР
=> ФР![]() сходится равномерно на множестве Е
сходится равномерно на множестве Е
Кроме того ФР ![]() сходится к некоторой к функцииS(x)
На множестве Е.
сходится к некоторой к функцииS(x)
На множестве Е.
![]()
Билет 6. Свойства равномерно сходящихся ФП и рядов: непрерывность.
Теорема.
Пусть ФП ![]() Определена в
Определена в![]() и пусть выполнены свойства.
и пусть выполнены свойства.
1) Все члены последовательности ![]() непрерывны в точке
непрерывны в точке![]()
2) ФП ![]() сходится равномерно к
сходится равномерно к![]() в
в![]() тогда функция
тогда функция![]() определенна в точке
определенна в точке![]()
Тогда функция ![]() непрерывна в точке
непрерывна в точке![]() .
.
Замечание :
Из доказательства теоремы будет видно, что справедливо утверждение.
Утверждение.
Пусть ФП ![]() Сходится равномерно к
Сходится равномерно к![]() на <а,b> и все члены
последовательности
на <а,b> и все члены
последовательности![]() непрерывны на <а,b>
тогда
непрерывны на <а,b>
тогда![]() непрерывна на <а,b>.
непрерывна на <а,b>.
Доказательство.(Теоремы о непрерывности).
![]() в
в![]() . Фиксируем
. Фиксируем![]() .
Для
.
Для![]()
![]()
![]() =>
=>
в частн. ![]()
![]() если
если![]()
Фиксир. ![]() соотв.
соотв.![]() непр. В т.
непр. В т.![]() => для
=> для![]()
![]()
![]()
![]()
Рассм. ![]() <
<![]() +
+![]()
Где n– зафиксирован.
Если![]() => функция
=> функция![]() непрерывна в т.
непрерывна в т.![]()
![]()
Теорема
Пусть ФР ![]() сходится равномерно в
сходится равномерно в![]() и все члены ряда
и все члены ряда![]() непрерывны в т.
непрерывны в т.![]() Тогда
сумма ряда
Тогда
сумма ряда![]() непрерывна в т.
непрерывна в т.![]()
Доказательство.
Ряд ![]() сходится равномерно в
сходится равномерно в![]() => последовательность частичных сумм
=> последовательность частичных сумм![]() в
в![]()
Т.к. все функции ![]() непрерывны в т.
непрерывны в т.![]() Все частичные суммы
Все частичные суммы![]() непрерывны
в т.
непрерывны
в т.![]() Следовательно
Следовательно![]() непрерыв. В . .
непрерыв. В . .![]()
Билет 7. Почленное интегрирование функционального ряда
Пусть функциональный ряд ![]() сходится
равномерно на [a,b]
к функцииS(x),
все члены ряда непрерывны на [a,b],
тогда
сходится
равномерно на [a,b]
к функцииS(x),
все члены ряда непрерывны на [a,b],
тогда![]() 0,x
0,x![]() [a,b]
справедливо
[a,b]
справедливо![]() ;(*)
;(*)
Формула (*) можно переписать в виде ![]()
Доказательство.
Так как функция непрерывна на [a,b]
=> интегрируема на [a,b]
и на любом![]() 0,x]
0,x]![]() [a,b]
. Функциональный ряд
[a,b]
. Функциональный ряд![]() сходится
равномерно на [a,b]
к функцииS(x)
и все члены ряда непрерывны на [a,b]
=> сумма рядаS(x)
непрерывна на [a,b]
=> интегрируема на
сходится
равномерно на [a,b]
к функцииS(x)
и все члены ряда непрерывны на [a,b]
=> сумма рядаS(x)
непрерывна на [a,b]
=> интегрируема на![]() 0,x]
0,x]![]() [a,b].
Нужно доказать, что ряд
[a,b].
Нужно доказать, что ряд![]() сходится к функции
сходится к функции![]()
![]() x
x![]() [a,b]. Рассмотрим
[a,b]. Рассмотрим![]() -
-![]() ={по свойству линейностиопр.
интегралов}=
={по свойству линейностиопр.
интегралов}=
![]() -
-![]() ={по
свойству линейности}=
={по
свойству линейности}=![]() -
-![]() =
=![]() -
-![]()
Фиксируем ![]() .
Ряд
.
Ряд![]() сходится равномерно на [a,b]
=>
сходится равномерно на [a,b]
=>
для ![]() >0,
>0, ![]() .;
.;
![]() =
=![]() ,
то есть
,
то есть
![]() .=>
.=>
![]() =>
ряд
=>
ряд ![]() сходится к
функции
сходится к
функции ![]() ,
,
![]() ▲.
▲.
8. Почленное дифференцирование функционального ряда
Теорема:
Пусть функциональный ряд
![]() определен на
определен на![]() и
выполнены условия:
и
выполнены условия:
Ряд
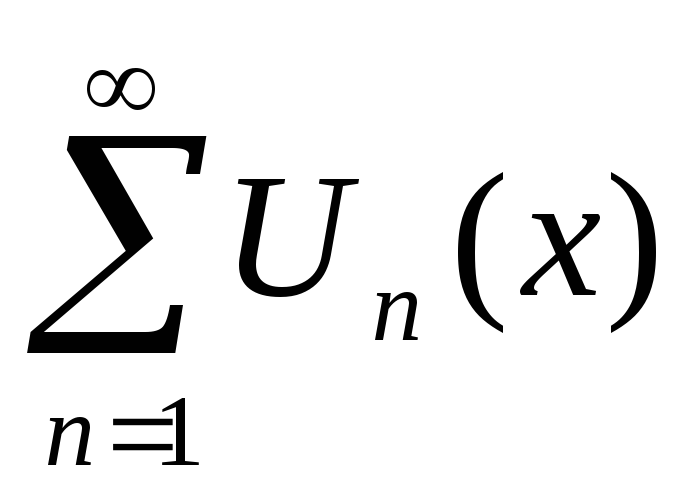 сходится по крайней мере в точке
сходится по крайней мере в точке
Все члены ряда
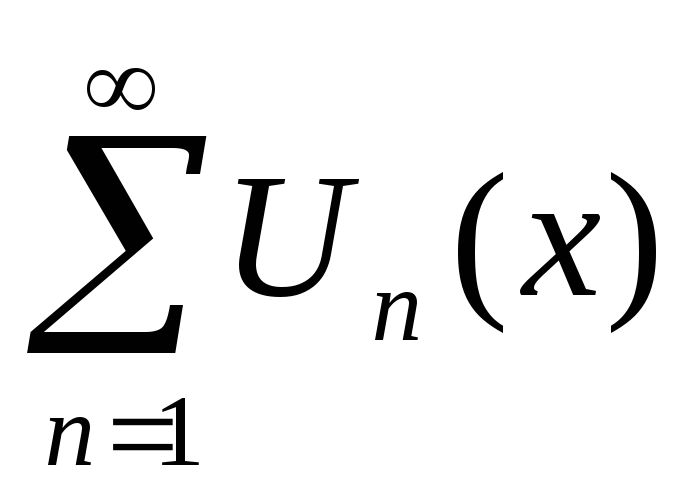 непрерывно дифференцируемы на
непрерывно дифференцируемы на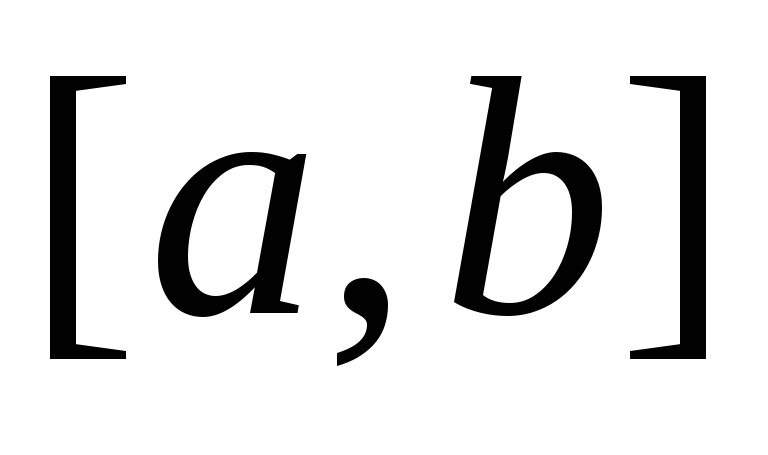
Ряд
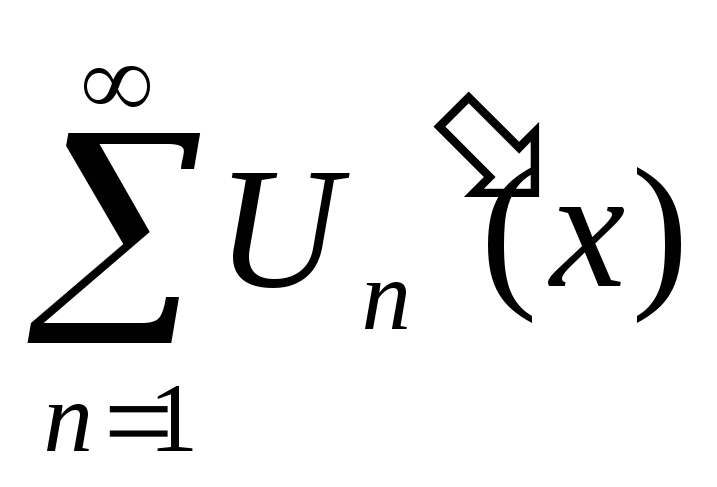 сходится равномерно на
сходится равномерно на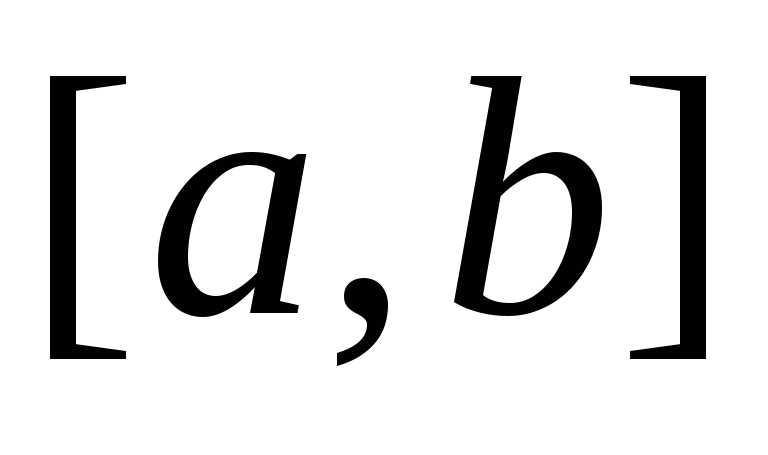
Тогда функц ряд
![]() сходится на
сходится на![]() ,
его суммаS(x)
непр. дифф-ма на
,
его суммаS(x)
непр. дифф-ма на![]() иS(x)
=
иS(x)
=![]()
![]() (*)
(*)
Формулу (*) можно записать в виде
![]() =
=![]()
Доказательство:
Обозначим
![]()
![]() .
Ф-ции
.
Ф-ции![]() непр на
непр на![]() и
и![]() сходится равномерно на
сходится равномерно на![]() =>G(x) непр
на
=>G(x) непр
на![]() .
По теореме о почленном интегрировании
для
.
По теореме о почленном интегрировании
для
![]()
![]() (по
формуле Ньютона-Лейбница)
(по
формуле Ньютона-Лейбница)![]() => ряд
=> ряд![]() сходится
сходится
![]() .
Т.к. функциональный ряд
.
Т.к. функциональный ряд![]() сх-ся в т.с=> сх-ся числ ряд
сх-ся в т.с=> сх-ся числ ряд![]() => для
=> для
![]() сх-ся ряд
сх-ся ряд![]()
![]() =>
=>![]() сх-ся
сх-ся
![]() =>
=>
![]()
![]()
![]() =
=![]() =>
=>
![]()
![]()
![]()
G(x) непр на![]() =>
=>
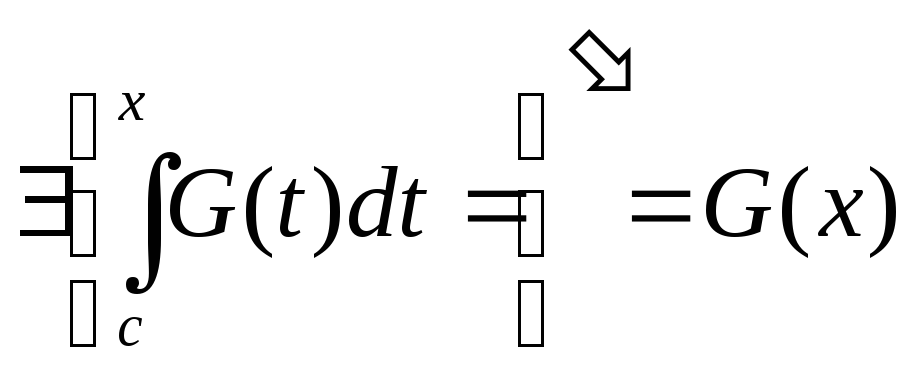 =>
=>![]()
![]() и
и
![]()
![]() .
Кроме того ф-яG(x)
непр на
.
Кроме того ф-яG(x)
непр на![]() =>
=>
![]() непр
на
непр
на![]() =>S(x) непр
дифф-ма на
=>S(x) непр
дифф-ма на![]() .▲
.▲
Билет №9 Степенной ряд. Теорема Абеля.
Функциональный ряд вида:
С0+С1(x-x0)+C2(x-x0)2+…+Cn(x-x0)n+…=![]()
где x0 и С0 , С1… Cn– заданные числа, называетсястепенным рядом
Степенной ряд сходится в точке х= x0
Задача – исследовать степенной ряд на сходимость в х
С помощью замены t= х- x0данный степенной ряд можно привести к виду
С0+С1t+C2t2+…+Cntn…
Поэтому далее рассматриваем степенной ряд:
С0+С1t+C2t2+…+Cntn+…=![]()
Теорема(Абеля):
Пусть степенной ряд
![]() сходится в точке x10.
Тогда ряд сходитсях:
|x|<| x1|
сходится в точке x10.
Тогда ряд сходитсях:
|x|<| x1|
Док-во
Ряд
![]() сх-ся в точке x1=>числовой ряд
сх-ся в точке x1=>числовой ряд![]() сх-ся => числовая последовательность
сх-ся => числовая последовательность![]() сх-ся (к нулю) => посл-ть
сх-ся (к нулю) => посл-ть![]() - ограничена, т.е.М:n
- ограничена, т.е.М:n![]() Рассмотримх: |x|<|
x1| Обозначим
Рассмотримх: |x|<|
x1| Обозначим![]()
Рассмотрим
![]() :
:![]()
Т.к. 0<q<1 =>![]() сх-ся=>числовой ряд (для фиксированных
х)
сх-ся=>числовой ряд (для фиксированных
х)![]() сх-ся по признаку сравнения. Т.к. х –
произвольная точка, т.ч. |x|<| x1|
Функциональный ряд
сх-ся по признаку сравнения. Т.к. х –
произвольная точка, т.ч. |x|<| x1|
Функциональный ряд![]() сх-ся на множестве |x|<| x1| =>
сх-ся на множестве |x|<| x1| =>![]() сх-ся абсолютно на множестве |x|<| x1|▲.
сх-ся абсолютно на множестве |x|<| x1|▲.
Следствие:
Если степенной ряд
![]() расходится
в точке x2 , то этот ряд расходитсях: |x|>| x2|
расходится
в точке x2 , то этот ряд расходитсях: |x|>| x2|
Док-во:
От противного: Пусть x3 : | x3|>| x2| и ряд сх-ся в точке x3 => по теореме Абеля ряд сх-ся в точке x2 – противоречие, т.к. в x2 ряд расходится=>ряд расходитсях: |x|>| x2|▲.
Билет №10 Радиус сходимости степенного ряда (теорема о существовании радиуса). Формула Коши – Адамара (без док-ва).
Определение:
Если R – неотрицательное число или
![]() ,
обладает тем свойством, что степенной
ряд
,
обладает тем свойством, что степенной
ряд![]() сходится на множестве |x|>R, то R называется
радиусом сходимости данного степенного
ряда. В этом случае интервал (-R;R) называется
интервалом сходимости этого степенного
ряда. Область сходимости степенного
ряда может не совпадать с интервалом
сходимости, т.к. может включать точки
сходится на множестве |x|>R, то R называется
радиусом сходимости данного степенного
ряда. В этом случае интервал (-R;R) называется
интервалом сходимости этого степенного
ряда. Область сходимости степенного
ряда может не совпадать с интервалом
сходимости, т.к. может включать точки![]()
Теорема:
У всякого степенного ряда есть радиус сходимости
Док-во:
Пусть А – множество всех неотрицательных
чисел, в которых степенной ряд
![]() сходится. Т.к. ряд сходится в т. х=0 =>
сходится. Т.к. ряд сходится в т. х=0 =>![]() =>supА (возможно равная
=>supА (возможно равная![]() )
)
Обозначим R=supA Докажем, что R – радиус сходимости степенного ряда:
Фиксируем x: |x|<R
=> по опр. supчисло![]() :
|x|<c<R
:
|x|<c<R
Т.к.
![]() =>
ряд сходится в точке с => по теореме
Абеля ряд сходится на множестве |x|<c,
в частности, сходится в точке x, т.к. х –
произвольная точка такая что |x|<R =>
ряд сходится на множестве |x|<R
=>
ряд сходится в точке с => по теореме
Абеля ряд сходится на множестве |x|<c,
в частности, сходится в точке x, т.к. х –
произвольная точка такая что |x|<R =>
ряд сходится на множестве |x|<R
Фиксируем x: |x|>R =>число b: |x|>b>R Т.к. b>R => bA, т.е. степенной ряд расходится в точке b => ряд расходится в точке х (по следствию из теоремы Абеля) Т.к. х – произвольная точка такая что |x|>R => ряд расходится на множестве |x|>R
Следовательно R=supA – радиус сходимости степенного ряда
Вопрос:как найти радиус сходимости степ. ряда?
Предположим, что
![]() конечный или бесконечный
конечный или бесконечный
Возможны 3 случая:
1) конечный![]() Обозначим
Обозначим![]()
Применим к ряду
![]() признак Даламбера:
признак Даламбера:
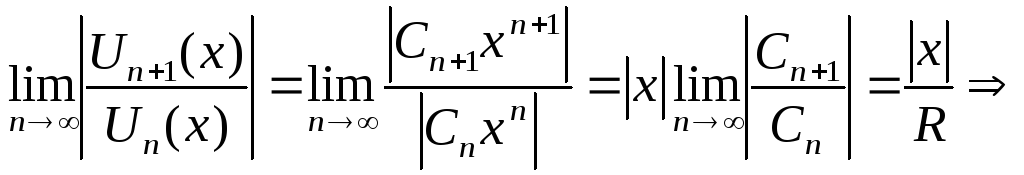 при
при![]() <1
– ряд сх-ся => исходный ряд
<1
– ряд сх-ся => исходный ряд![]() сх-ся(абсолютно) на мн-ве |x|<R
сх-ся(абсолютно) на мн-ве |x|<R
Если![]() >1
– не выполнен необходимый признак сх-ти
ряда => ряд рас-ся на множестве |x|>R =>
R=
>1
– не выполнен необходимый признак сх-ти
ряда => ряд рас-ся на множестве |x|>R =>
R=![]() - радиус сх-ти степенного ряда в случае
1)
- радиус сх-ти степенного ряда в случае
1)
2)
![]() =0
Если
=0
Если![]() n, то посл-ть {
n, то посл-ть {![]() }
– бескон. большая, т.е.
}
– бескон. большая, т.е.![]() =
=![]() Рассмотрим:
Рассмотрим:
![]() если
х0 => если х0,
то не выполнен необходимый признак
сх-ти ряда => ряд рас-сяx0
=>радиус сх-ти R=0 в случае 2)
если
х0 => если х0,
то не выполнен необходимый признак
сх-ти ряда => ряд рас-сяx0
=>радиус сх-ти R=0 в случае 2)
3)
![]() =
=![]() =>посл-ть {
=>посл-ть {![]() }
– б.б. => посл-ть {
}
– б.б. => посл-ть {![]() }
– б.м.=>
}
– б.м.=>![]() =>
=>![]() х => по признаку
Даламбера ряд сх-ся(абсолютно)х
=>R=
х => по признаку
Даламбера ряд сх-ся(абсолютно)х
=>R=![]() =
=![]() в случае 3)
в случае 3)
Т.О. если
![]() =>радиус
сх-ти степенного ряда R=
=>радиус
сх-ти степенного ряда R=![]()
Анал-но доказывается, что если
![]() (конечный или бесконечный) то радиус
сх-ти степенного ряда R=1/
(конечный или бесконечный) то радиус
сх-ти степенного ряда R=1/![]() где полагаем что R=0 при
где полагаем что R=0 при![]() и R=
и R=![]() при
при![]()
В общем случае справедлива формула
Коши-Адамара:
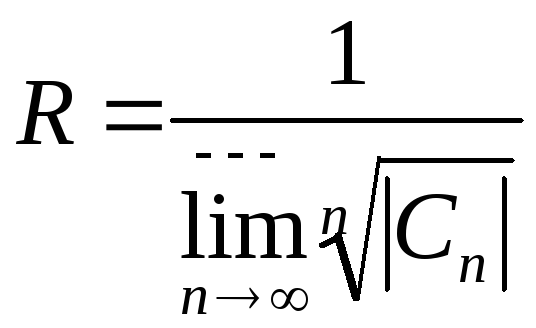
Билет 11. Равномерная сходимость степенных рядов. Непрерывность суммы степенного ряда.
Теорема
Если степенной ряд ![]() *
*![]() имеет радиус сходимостиR>0,
то данный ряд сходится равномерно на
любом отрезке [-r;r],
где 0<r<R.
имеет радиус сходимостиR>0,
то данный ряд сходится равномерно на
любом отрезке [-r;r],
где 0<r<R.
Доказательство:
Рассмотрим ![]() r:
0<r<R=>r
r:
0<r<R=>r![]() (-R;R) => в
точкеx=rстепенной ряд сходится абсолютно, т.е.
числовой ряд
(-R;R) => в
точкеx=rстепенной ряд сходится абсолютно, т.е.
числовой ряд![]() *
*![]() .
Справедливо неравенство
.
Справедливо неравенство
![]() =
=![]() *
*![]() ,
,![]()
![]() [-r;r] => так
как числовой ряд
[-r;r] => так
как числовой ряд![]() *
*![]() сходится, то по признаку Вейерштрасса
данный степенной ряд сходится равномерно
на [-r;r]
сходится, то по признаку Вейерштрасса
данный степенной ряд сходится равномерно
на [-r;r]![]()
Замечание:
Из теоремы не следует, что ряд сходится равномерно на (-R;R), гдеR– радиус сходимости.
Пример:
Ряд ![]() 1) сходится равномерно на
1) сходится равномерно на![]() [-r;r],r<1; 2) не
сходится равномерно на (-1, 1) .
[-r;r],r<1; 2) не
сходится равномерно на (-1, 1) .
Теорема(непрерывность суммы)
Если степенной ряд ![]() *
*![]() имеет
радиус сходимостиR>0,
то сумма рядаS(x)
непрерывна на (-R; R)
имеет
радиус сходимостиR>0,
то сумма рядаS(x)
непрерывна на (-R; R)
Доказательство:
Нужно доказать, S(x)
непрерывна в![]() (-R;R). Фиксируем
(-R;R). Фиксируем![]() x
x![]() (-R;R) =>
(-R;R) =>![]() => из теоремы 1 следует, что данный ряд
сходится равномерно на [-r;r]. Кроме того, все члены
ряда (
=> из теоремы 1 следует, что данный ряд
сходится равномерно на [-r;r]. Кроме того, все члены
ряда (![]() *
*![]() – непрерывны на [-r;r].
=> по теореме о непрерывности равномерного
сходящегося функционального ряда
получаем, чтоS(x)
непрерывна на [-r;r]
=>S(x)
непрерывна в точкеx, так
какx
– непрерывны на [-r;r].
=> по теореме о непрерывности равномерного
сходящегося функционального ряда
получаем, чтоS(x)
непрерывна на [-r;r]
=>S(x)
непрерывна в точкеx, так
какx![]() [-r;r]
[-r;r]![]()
Билет №12. Интегрирование степенных рядов.
Пусть степенной ряд ![]() имеет радиус сходимостиR>0.
Тогда
имеет радиус сходимостиR>0.
Тогда![]() x
x![]() (-R,R)
(-R,R)
![]() =
=![]() (1) причем радиус сходимости степенного
ряда в правой части (1) также равенR.
(1) причем радиус сходимости степенного
ряда в правой части (1) также равенR.
Доказательство:
Фиксируем ![]() x
x![]() (-R,R) =>
(-R,R) =>![]() :
|x| <R=>
ряд
:
|x| <R=>
ряд![]() сходится равномерно наx
сходится равномерно наx![]() [-r,r]
[-r,r]
и все члены ряда непрерывные на [-r,r] функции. Следовательно, по теореме о почленом интегрировании функционального ряда имеем:
![]() =
=![]() =
=![]() Пусть
Пусть![]() – радиус сходимости ряда
– радиус сходимости ряда![]() =>
=>![]() ;
;![]() = =
= =![]() =
=![]() так как
так как
R = ![]() =>
=> ![]()
Билет 13. Дифференцирование степенных рядов.
Теорема :
Пусть степенной ряд ![]() имеет радиус сходимости R>0. Тогда дляx(-R;R):
имеет радиус сходимости R>0. Тогда дляx(-R;R):
(![]() )’
=
)’
=![]() (*),
(*),
причем радиус сходимости ряда в правой части (*) равен R.
Док-во:
Пусть R1- радиус сходимости ряда
в правой части (*) =>R1=![]()
![]()
=>R1=R
Фиксируем x(-R;R).
Тогда r>0:
|x|<r<R => [-r;r][-R;R] => ряд сходится равномерно на [-r;r];
Все функции непрерывно дифференцируемы на [-r;r];
Исходный ряд ![]() сходится на [-r;r] => по теореме о почленном
дифференцировании функционального
ряда (на всем отрезке [-r;r]):
сходится на [-r;r] => по теореме о почленном
дифференцировании функционального
ряда (на всем отрезке [-r;r]):
(![]() )’
=
)’
=![]() =
=![]() .
Так какточкаx[-r;r]=>
в точкеx
.
Так какточкаx[-r;r]=>
в точкеx
![]() =
=![]()
Билет 14. Ряд Тейлора. Условия разложения функции в ряд Тейлора.
Определение.
Пусть f(x) имеет в точкеx0 производные любого порядка. Составим формально ряд:
![]()
Этот ряд называется рядом Тейлора функции f(x) с центром в точкеx0.
Если x0 =0, то ряд Тейлора называют рядом Макларена.
Вопрос: При каких условиях на функцию f(x) ряд сходится к функцииf(x)?
Пусть f(x) имеет производные любого порядка вU(x0). Тогдаf(x) можно разложить по формуле Тейлора вU(x0), то есть:
=![]() ;xU(x0),
гдеRn(x)
– остаточный член формулы Тейлора (но
не остаток ряда!!)
;xU(x0),
гдеRn(x)
– остаточный член формулы Тейлора (но
не остаток ряда!!)
![]() =
=![]() n-ая частичная сумма ряда
Тейлора
n-ая частичная сумма ряда
Тейлора
=> f(x)=Sn(x)+ Rn (x); xU(x0)
Ряд Тейлора сходится к функции f(x)
<=>![]() ,xU(x0)
<=>
,xU(x0)
<=>
![]() ,xU(x0);
,xU(x0);
Таким образом ряд Тейлора функции f(x) сходится к функцииf(x) вU(x0) <=>
Для остаточного члена формулы Тейлора справедливо:
![]() ;xU(x0);
;xU(x0);
Если ряд Тейлора функции f(x) сходится к функцииf(x) вU(x0), то
![]() ,
,
то есть Rn(x)=rn(x).
Действительно:
![]() ;
;
Cдругой стороны:f(x)=Sn(x)+Rn(x)
=> Rn(x)=rn(x)
Теорема: (достаточное условие разложения функции в ряд Тейлора)
Пусть функция f(x) имеет вU(x0) производные любого порядка, причем все производныеf(n)(x) ограничены в совокупности вU(x0), то естьM>0n=0,1,2,…xU(x0)
| f(n)(x0) |M
Тогда f(x) можно разложить в ряд Тейлора вU(x0):
![]() ;
x
U(x0);
;
x
U(x0);
Это значит, что ряд Тейлора сходится к функции f(x).
Док-во:
Достаточно доказать, что остаточный
член формулы Тейлора ![]() ,xU(x0);
,xU(x0);
Так как функция f(x) имеет производные любого порядка вU(x0), тоf(x) можно записать по формуле Тейлора с остаточным членом в форме Лагранжа, то есть:
![]() ,
гдележит междуxиx0.
,
гдележит междуxиx0.
| Rn
(x)|=![]() ;
x
U(x0);
;
x
U(x0);
Расмотрим числовой ряд: ![]() ;
;
По признаку Даламбера числовой ряд сходится, т.к. :
![]()
Тогда выполнен необходимый признак сходимости ряда:
![]() ;
Тогда:
;
Тогда:![]() ,xU(x0)
,xU(x0)
Билет 15. Разложение элементарных функций в ряд Тейлора.
![]()
![]()
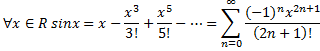
2. ![]()
![]() => аналогично получаем разложение для
=> аналогично получаем разложение для![]()
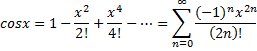
3. ![]()
![]() .
Фиксируем для
.
Фиксируем для![]() ,n=0,1…
,n=0,1…![]() =>
=>![]() в частности справедливо в точкеx,
т.к х произвольная точка из R =>
в частности справедливо в точкеx,
т.к х произвольная точка из R =>
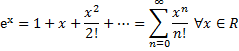
4.
![]() .
.![]()
![]()
Записываем остаточный член формулы
Тейлора функции ![]() в форме Коши, можно доказать, что
в форме Коши, можно доказать, что![]()
![]()
В частности ![]()
![]() ,
,![]()
5. ![]()
![]() ряд Тейлора для функции
ряд Тейлора для функции![]()
![]()
Радиус сходимости : ![]()
В точке х=-1 получаем числовой ряд: ![]()
Докажем что остаточный член формулы
Тейлора ![]()
![]()
Пусть ![]() Запишем
остаточный член в форме Лангранжа
Запишем
остаточный член в форме Лангранжа![]()
![]()
![]()
![]()
![]()
![]()
![]()
Аналогично, записывая ![]() в форме Коши, можно доказать, что
в форме Коши, можно доказать, что![]()
![]()
Таким образом, ![]()
![]()
Билет 16. Ортогональность тригонометрической системы функций. Тригонометрический ряд Фурье. Теорема Дирихле.
В пространстве кусочно-непрерывных на
![]() функций рассмотрим тригонометрическую
систему функций:
функций рассмотрим тригонометрическую
систему функций:
![]() Эта
система является ортогональной на
Эта
система является ортогональной на![]() т.к.
т.к.
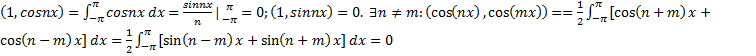
![]() Коэффициенты тригонометрического рядя
Фурье
Коэффициенты тригонометрического рядя
Фурье
[ ![]() – формально ряд Фурье
– формально ряд Фурье![]() -
коэффициент ]
-
коэффициент ]
![]() // скалярное произведение //
// скалярное произведение //
(1,1)=![]()
![]() =
=![]()
![]()
![]()
![]()
Формальный ряд ![]()
Теорема Дирихле.
Пусть ![]() -периодическая
функция, кусочно-непрерывная и
кусочно-монотонная на
-периодическая
функция, кусочно-непрерывная и
кусочно-монотонная на![]() .
Тогда тригонометрический ряд Фурье
сходится везде на
.
Тогда тригонометрический ряд Фурье
сходится везде на![]() причем для его суммы
причем для его суммы![]() справедливы равенства: 1)
справедливы равенства: 1)![]() Если
Если![]()
2)![]()
![]()
![]()
3)![]()
![]()
Определение.
![]() называется кусочно-монотонной на
называется кусочно-монотонной на![]() если
если![]() можно разбить на конечное число
промежутков, на каждом из которых функция
монотонна.
можно разбить на конечное число
промежутков, на каждом из которых функция
монотонна.
Определение.
Функция называется кусочно-непрерывной
на ![]() если она непрерывна на
если она непрерывна на![]() за исключением конечного числа точек
разрыва 1-ого рода.
за исключением конечного числа точек
разрыва 1-ого рода.
