Решение.
Заряд Q, который нужно поместить в нижней точке сферы, должен быть таким, чтобы электрическая, действующая на верхний заряд, была не меньше силы тяжести mg, т.е.
kQq/d2 ≥ mg.
Отсюда
Q ≥ mgd2/q.
О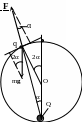
днако
нам нужно проверить, будет ли равновесие
шарика устойчивым. Рассмотрим малое
отклонение шарика от положения равновесия.
Равновесие устойчиво, если проекция
силы F электрического взаимодействия
зарядов на касательную к сфере больше
или равна проекции силы тяжести на ту
же касательную:
kQqsinα/d2 ≥ mgsin2α.
(Сила N реакции перпендикулярна к поверхности сферы.) Так как угол α отклонения шарика от положения равновесия мал, то sinα ≈ α. Тогда условием устойчивого равновесия будет неравенство
Q ≥ 2mgd2/q.
6. Три одинаковых положительных точечных заряда q расположены в вершинах равностороннего треугольника. Сторона треугольника равна L. Найти напряженность в вершине тетраэдра, построенного на этом треугольнике.
Ответ: E = k√6q/L2.
Решение.
К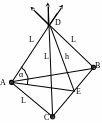
аждый
заряд создает в точке D напряженность
поля
Е/ = kq/L2.
Полная напряженность будет суммой трех векторов (см. рис.). Горизонтальные составляющие этих векторов в сумме дадут нуль, так как они равны по модулю и составляют друг с другом углы по 120о. Сами векторы образуют с вертикалью углы 90о – α, где α – угол между ребром тетраэдра и высотой h треугольника ABC. Вертикальные составляющие одинаковы и равны каждая
kqsinα/L2.
Из треугольника ADE очевидно, что
sinα = (2/3)1/2.
Отсюда искомая напряженность поля равна
E = k√6q/L2.
7. Четыре непроводящих шарика радиуса r = 10 –3 м, в центре каждого из которых находится заряд q = 10 –7 Кл, расположены вдоль прямой, касаясь друг друга. Какую работу нужно совершить, чтобы сложить из этих шариков пирамидку (правильный тетраэдр)? Влиянием силы тяжести пренебречь. (Меледин, 3.34)
Ответ: A = 0.07 Дж.
Решение.
Энергия цепочки
W1 = k[q2/6r + 2q2/4r + 3q2/2r] = 13kq2/6r.
Энергия тетраэдра
W2 = 3kq2/r.
Искомая работа
A = 5kq2/6r = 0.07 Дж.
8. Тонкое проволочное кольцо имеет заряд +Q. Маленький шарик массой m, имеющий заряд -q, может двигаться без трения по тонкой диэлектрической спице, проходящей вдоль оси кольца. 1) Как будет двигаться шарик, если его отвести от центра кольца на расстояние x << R и отпустить без начальной скорости? Записать уравнение движения шарика x(t). Как изменится движение, если убрать спицу? 2) Как будет двигаться шарик, если ему мгновенно придать скорость vo, направленную вдоль оси кольца? Как зависит характер движения от величины vo?(1001, 12.28,12.29).
Ответ: 1) Шарик будет совершать гармонические колебания x = xocos{[kxQq/(mR3)]1/2t}, 2) При vo ≥ vmin = [2kQq/(mR)]1/2 шарик уйдет на бесконечность; при vo < vmin – шарик будет совершать колебания (при vo << vmin – гармонические).
Решение.
На расстоянии х от центра кольца на шарик действует сила
F = qE = kxQq/[R2 + x2]3/2,
направленная к центру кольца. Поскольку R2 + x2 ≈ R2 при x << R, второй закон Ньютона для шарика принимает вид
max = - kxQq/R3.
Это – уравнение гармонических колебаний с циклической частотой
ω = [kxQq/(mR3)]1/2.
Максимальное отклонение хо достигается в начальный момент времени, так что
x = xocosωt = xocos{[kxQq/(mR3)]1/2t}.
Если убрать спицу, проявится неустойчивость такого движения по отношению к малым боковым смещениям, поэтому шарик притянется к какой-нибудь точке кольца.
Воспользуемся законом сохранения энергии
-qφ(0) + ½ mvo2 = -qφ(x) + ½ mv(x)2,
где φ(x) = kQ/(R2 + x2)1/2 – потенциал кольца на расстоянии x, v(x) – скорость шарика на расстоянии х от кольца. Если
-qφ(0) + ½ mvo2 ≥ 0,
то шарик улетит на бесконечность. При этом начальная скорость шарика должна удовлетворять условию
vo ≥ vmin = [2kQq/(mR)]1/2.
При vo < vmin – шарик будет совершать колебания (при vo << vmin – гармонические).
9. Заряд Q равномерно распределен по объему шара радиусом R из непроводящего материала. Чему равна напряженность и потенциал поля на расстоянии r от шара? Построить графики E(r) и φ(r). (1001,12.31,12,32)
Ответ: при r ≤ R: E(r) = k|Q|r/R3, φ(r) = ½ kQ(3R2 – r2)/R3; при r > R: E(r) = k|Q|/r2, φ(r) = kQ/r2