Решение.

Разложим скорость шарика v_o на тангенциальную (вдоль плиты) и нормальную (перпендикулярно к плите) составляющие:

v_oτ = v_osinα и v_on = v_o cosα .

Тангенциальная составляющая, благодаря гладкости стенки, после соударения шарика не изменяется. Нормальная составляющая относительно движущейся плиты

w_on = v_on + u = v_o cosα + u

после соударения изменит знак, сохранив свой модуль:

w_n = - w_on.

Относительно неподвижной системы отсчета составляющая нормальная составляющая v_n изменится на величину u:

v_n = w_n – u = -(v_o cosα + 2u).

Полная скорость шарика относительно неподвижной системы отсчета после соударения с плитой будет

v = (v_n² + v_oτ²)^1/2 = [(v_ocosα +2u)² + (v_osinα)²]^1/2.

.

14. По прямому шоссе со скорость v₁ = 16 м/с движется автобус. На расстоянии d = 60 м от шоссе и s = 400 м от автобуса находится человек. Человек может бежать со скоростью v₂ = 4 м/с. В каком направлении он должен бежать, чтобы “перехватить” автобус, который к нему приближается? При какой наименьшей скорости человека v_min это вообще возможно? В каком направлении следует при этом бежать?

Ответ: 37^о ≤ β ≤ 143^o, где β – угол, отсчитываемый от направления на автобус; v_min = 2.4 м/с, следует бежать перпендикулярно направлению на автобус.

Решение.

Р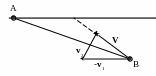 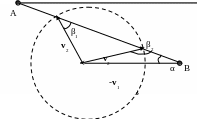ешение задачи становится проще и нагляднее, если перейти в систему отсчета, связанную с автобусом. В этой системе отсчета скорость человека V = v₂ – v₁. Величина скорости V роли не играет, а направление должно быть таким, чтобы человек пересек шоссе правее “стоящего” автобуса или, в крайнем случае, вышел точно на автобус (см. рис.). Конец вектора V лежит на окружности радиуса v₂ (см. рис.). Очевидно, угол β между отрезком АВ и направлением v₂ должен лежать в пределах β₁ ≤ β ≤ β₂ , где β₁ и β₂ – два решения уравнения

sin β = (v₁/v₂ )sinα

(уравнение следует из теоремы синусов), удовлетворяющие условию 0 < β < π. Здесь

sinα = d/s.

Таким образом

arcsin(v₁d/v₂s) ≤ β ≤ 180^o – arcsin(v₁d/v₂s) ; 37^о ≤ β ≤ 143^o.

Поскольку область решений соответствует условию

sin β ≥ (v₁/v₂ )sinα = dv₁/sv₂ ,

то

dv₁/sv₂ ≤ 1

или

v₂ ≥ dv₁/s.

Значит

v_min = dv₁/s = 2.4 м/с.

При такой скорости sin β = 1, β = 90^о – т. Е бежать нужно под прямым углом к направлению на автобус (а не к дороге).

15. Небольшое тело падает с высоты h на горизонтальную поверхность. При каждом соударении с поверхностью модуль скорости тела уменьшается в k раз. Найти полный путь, пройденный телом до остановки.

Ответ: S = h(1 + k²)/(1 – k²).

Решение

Путь, пройденный телом после i-го соударения, равен

S_i = v_i²/g = k²(v_i-1²/g) = k²S_i-1.

Таким образом, последовательность путей, пройденных телом после каждого соударения, представляет собой убывающую геометрическую прогрессию со знаменателем q = k² < 1. Первый член этой прогрессии равен S₁ = k²(v_o²/g) = 2hk².

Полный путь, пройденный телом равен

S = h + S_прогр

где S_прогр – сумма членов геометрической прогрессии

S_прогр = S₁(1 – qⁿ)/(1 –q).

При n → ∞

S_прогр = S₁/(1 –q) = 2hk²/(1 – k²).

Тогда для полного пути, пройденного телом до остановки, получим

S = h(1 + k²)/(1 – k²).

1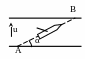 6. По реке из т. А в т. В вдоль прямой АВ, образующей угол с линией берега α, плывет катер. Под прямым углом к берегу дует ветер со скоростью u. Флаг на мачте катера образует угол β с направлением движения катера. Определить скорость катера относительно берега.

Ответ: v = - ucos(α + β)/sinβ.

Решение

Н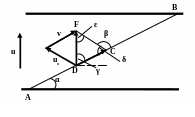 аправление флага совпадает с направлением скорости ветра относительно катера u_o. Из закона сложения скоростей u = v + u_o получим

u_o = v + u.

Из треугольника DFC

δ = π – β,

γ = ½ π – α,

ε = π – δ – γ =

= π – (π – β) – (½ π – α) = α + β - ½ π.

По теореме синусов

v/sinε = u/sinδ → v = u sinε /sinδ = u sin(α + β - ½ π) /sin(π – β) →

v = - u cos(α + β)/sinβ

1.2. Равноускоренное движение.

1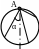 . Из точки А, лежащей на верхнем конце вертикального диаметра некоторой окружности радиуса R, по желобам, установленным вдоль различных хорд этой окружности (см. рис.), одновременно начинают скользить грузы. Через какое время грузы достигнут окружности? Как это время зависит от угла α наклона хорды к вертикали? Трением пренебречь.

Ответ: t = 2(R/g)^1/2.

Решение.

Время движения t груза вдоль хорды определяется из соотношения

t² = 2L/a,

где а – ускорение груза, L – длина хорды. Если хорда составляет с вертикалью угол α, то

a = gcosα,

L = 2Rcosα,

где R – радиус окружности. Таким образом,

t² = 4R/g.

Время движения грузов вдоль любой из хорд будет одинаковым.

2. Тело начинает двигаться из состояния покоя прямолинейно с постоянным по величине ускорением. Через некоторое время ускорение меняет свой знак, оставаясь прежним по величине. Найти отношение величины максимальной скорости v₁, которая была у тела при удалении от точки старта, к величине скорости v₂, с которой оно вернулась в точку старта.

Ответ: v₁/v₂ = 1/√2.

Решение.

При движении “туда” максимальная скорость тела определяется из соотношения:

v₁² = 2aS,

где а – ускорение тела, S – пройденный им путь.

При движении обратно максимальная скорость тела определяется из равенства

v₂² – v₁² = 2aS.

Отсюда получаем искомое соотношение

v₁/v₂ = 1/√2.

3. Лифт начинает подниматься с ускорением а = 2.2 м/с². Когда его скорость достигла v = 2.4 м/с, с потолка кабины лифта начал падать болт. Чему равны время t падения болта и перемещение болта при падении относительно земли? Высота кабины лифта Н = 2.5 м.

Ответ: t = 0.645c , s = 0.49 м.