Решение.

За время Δt насос подает на высоту Н массу воды ρVΔt , совершая работу А, равную изменению механической энергии воды. Так как насос “гонит” воду с некоторой скоростью v, то

A = ½ (ρVΔt)v² + (ρVΔt)gH.

Следовательно, мощность насоса

N = ½ ρVv² + ρVgH.

Найдем скорость v. За время Δt через поперечное сечение трубы площадью S = ¼ πd² проходит объем воды VΔt = vΔt(¼ πd²). Отсюда

v = 4V/ (πd²).

Таким образом, мощность насоса

N = 32ρV³/ (π²d⁴) + ρVgH.

Из последнего выражения видно, что чем больше диаметр d трубы, тем меньше необходимая мощность насоса. Но можно уменьшить величину N , не меняя диаметра трубы. Если обрезать на высоте h << H, то вода будет вылетать из трубы с некоторой скоростью u. Для этого необходима мощность насоса

N^/ = ½ ρVu²

(т.к. h <<H, то потенциальной энергией на высоте h для простоты пренебрегаем). Для того чтобы вода поднялась на высоту Н, необходимо, чтобы ее скорость была не меньше, чем

u_min = [2g(H – h)]^1/2 ≈ [2gH]^1/2.

Таким образом, можно использовать насос мощностью

N^/ = ρVgH.

2. Водометный катер забирает забортную воду и выбрасывает ее назад со скоростью u = 20 м/с относительно катера. Площадь поперечного сечения струи S = 0.01 м². Найти скорость катера, если действующая на него сила сопротивления пропорциональна квадрату скорости: F = kv², причем k = 7.5 Н^.с²/м² . (Козел, 1.68)

Ответ: v = 13.4 м/с.

Решение.

Масса воды, которую в единицу времени забирает и выбрасывает катер m_t = ρSu. Когда вода забирается в катер, она приобретает скорость катера v, и на катер (по третьему закону Ньютона) действует сила

F₁ = - ρSuv.

Когда вода выбрасывается из катера назад со скоростью u, на катер действует сила

F₂ = ρSu² .

Результирующая сила, действующая на катер со стороны воды,

F = F₁ + F₂ = ρSu(u – v).

Она равна силе сопротивления, так как катер по условию движется с постоянной скоростью:

ρSu(u – v) = kv².

Решая квадратное уравнение, находим v = 13.4 м/с.

3. На высоте h = 2 м над широким сосудом открывают на время t_o = 2 с кран, из которого вниз выливается в единицу времени масса воды m_t = 0.2 кг/с. Площадь отверстия крана S = 1см². Найти изменение силы давления на подставку и изобразить графически эту силу как функцию времени. (Козел, 1.72)

Решение.

Скорость, с которой вода вытекает из крана,

v_o = m_t /ρS = 2 м/с.

Скорость v, которую имеет вода, попадая в сосуд, можно найти с помощью закона сохранения энергии:

v = (v_o + 2gh)^1/2 = 6.6 м/с.

При попадании в сосуд вода тормозится, происходит абсолютно неупругий удар, вследствие чего на сосуд действует сила, равная изменению импульса в единицу времени:

F₁ = m_t v = 1.3 Н.

Кроме того, по мере заполнения сосуда водой на дно действует сила тяжести этой воды, линейно нарастающая со временем:

F ₂ = m_t gt.

Общая сила давления на дно

F = F₁ + F₂ .

Ее график приведен на рисунке. Время, за которое вода долетает от крана до сосуда,

t₁ = 2h/ (v + v_o) = 0.45 с.

Начальную силу давления на дно полагаем равной нулю. Максимальная сила давления на дно

F_max = F₁ + m_t gt_o = 5.2 H.

Сила давления на дно сосуда после того, как струя перестанет попадать в сосуд

F_к = m_t gt_o .

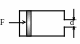4 . Цилиндр диаметра D заполнен водой и расположен горизонтально (см. рис.). С какой скоростью перемещается поршень, если на него действует сила F, а из отверстия в задней стенке цилиндра вытекает струя диаметра d? Трением пренебречь силу тяжести не учитывать. (Козел, 1.74)

Ответ: v = (2d²/D){2F/[πρ(D⁴ – d⁴)]}^1/2.