Решение.

Введем оси координат х₁ и х₂. Второй закон Ньютона в проекциях на эти оси запишется в виде

Т₁ – m₁gsinα = m₁a₁,

m₂g – T₂ = m₂a₂.

Из условия невесомости блока следует

Т₂ = 2Т₁.

Далее, запишем уравнение кинематической связи – за равные промежутки времени модуль перемещения тела m₂ вдвое меньше модуля перемещения тела m₁.

а₁ = 2а₂.

С учетом этого, для ускорений тел получим

a₂ = g(m₂ – 2m₁sinα)/(4m₁ + m₂) = 0.5 g.

a₂ = 2a₁ = g.

11. Ледяная горка составляет с горизонтом угол α = 30^о, по ней пускают снизу вверх камень, который в течение времени t₁ = 2c проходит расстояние S = 16м, после чего соскальзывает вниз. Какой промежуток времени t₂ длится проскальзывание камня вниз? Каков коэффициент трения между горой и камнем?

Ответ: t₂ = 4.2c, k = 0.37.

Решение

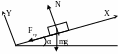
Направим оси координат, как показано на рисунке (такой выбор удобен, как правило, всегда, когда речь идет о наклонной плоскости). Второй закон Ньютона в проекциях на оси координат запишется в виде:

X: - F_тр – mgsinα = ma_x^u - при движении вверх,

F_тр – mgsinα = ma_x^d - при движении вниз,

Y: N - mgcosα = 0.

F_тр = kN = kmgcosα.

С другой стороны, кинематические уравнения кинематические движения камня можно записать в виде

S = ½ a_x^u t₁²,

- S = ½ a_x^d t₂².

Решая эти уравнения, получим

t₂ = t₁[S/(gt₁²sinα – S)] = 4.2 c.

k = {[2S/ t₁² – gsinα]/gcosα} = 0.37.

2.2. Вращательное движение.

1. На горизонтальном диске, на расстоянии R от оси лежит маленькая шайба. Диск медленно раскручивают так, что его угловая скорость равномерно возрастает со временем. Через время τ после начала раскручивания шайба начала скользить по диску. Найти коэффициент трения шайбы о диск, если за время τ диск сделал n оборотов. (МГУ, физ. фак. , 2000)

Ответ: /

Решение.

При раскручивании диска сила трения сообщает шайбе ускорение. По второму закону Ньютона

,

где - полное ускорение шайбы;

нормальное (центростремительное) ускорение, связанное с изменением направления вектора скорости;

тангенциальное ускорение, связанное с изменением модуля скорости. Поскольку , то .

В момент, когда шайба начала скользить по диску . Следовательно .

Из кинематических соотношений

; ; ,

где путь, пройденный шайбой по окружности,

модуль скорости шайбы по истечению времени . Получим

, .

Отсюда искомый коэффициент трения будет равен

/ .

2. Спутник вращается по круговой орбите вокруг Земли на высоте h = 3200 км. В какой пропорции сообщенная ему при запуске энергия поделилась между потенциальной и кинетической энергиями?

Ответ: W_П/W_K = 1.

Решение.

Кинетическую энергию спутника W_K = ½ mv² несложно найти, используя второй закон Ньютона и закон всемирного тяготения

mv²/(R + h) = GmM/(R + h)² → v² = (GM/R²)R² /(R + h) → v² = gR² /(R + h).

W_K = ½ mv² = ½ mgR² /(R + h).

Здесь m, M – массы спутника и Земли, R – радиус Земли, G – гравитационная постоянная, g = GM/R² – ускорение свободного падения.

Находясь на поверхности Земли, спутник уже обладает потенциальной энергией. Если, как обычно, выбрать начало отсчета потенциальной энергии на бесконечности, то для потенциальной энергии тела, находящегося на расстоянии r от Земли, можно записать

W = - GMm/r = - mgR²/r.

Потенциальная энергия на поверхности Земли будет

W_П⁽¹⁾ = - mgR,

а потенциальная энергия на орбите

W_П⁽²⁾ = - mgR²/(R + h).

Следовательно, при выводе спутника на орбиту ему была сообщена потенциальная энергия

W_П = W_П⁽²⁾ - W_П⁽¹⁾ = mghR/(R + h).

Тогда

W_П/W_K = 2h/R = 1.

3. На бруске, находящемся на горизонтальной плоскости, вертикально установлен легкий стержень, к которому привязана нить с грузом массы m = 100 г на конце (см. рис.). Нить с грузом отклоняют до горизонтального положения и отпускают. Определить массу бруска, если он сдвинулся, когда угол между нитью и стержнем был равен α = 45^о. Коэффициент трения бруска о плоскость k = 0.8. (МАИ,1999)

Ответ: M = 37.5 г.