Решение.
В момент времени t, когда скорость груза становится равной v(t) , точно такую же по величине линейную скорость должна иметь и любая точка тонкого обода. Следовательно, кинетическая энергия системы “колесо-груз” должна стать равной
Wk = ½ (M + m)v2.
На основании закона сохранения механической энергии можно записать
½ (M + m)v(t)2 = mgh(t).
Величину тангенциальной составляющей ускорения обода можно считать равной ускорению груза
v(t) = aτ t ; h(t) = ½ aτ t2.
Подставляя эти соотношения в предыдущие уравнение, получим:
aτ = mg/(m + M).
Учитывая, что нормальная составляющая ускорения равна
an = v2/R,
определим полное ускорение точек обода в момент времени t:
a = (an2 + aτ2)1/2 = mg{R2 + [mgt2/(M + m)]2}/[(M + m)R].
3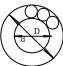
.
Шарикоподшипник поддерживает конец
оси вала, вращающегося с угловой скоростью
ω. Диаметр оси вала равен d
, диаметр обоймы шарикоподшипника равен
D
(см. рис.). Найти линейную скорость
движения центра одного из шариков, если
обойма неподвижна и если обойма вращается
с угловой скоростью Ω. Считать, что в
обоих случаях шарики катятся по валу и
обойме без проскальзывания.
Ответ: vo = ½ (v1 + v2) = (ωd + Ω D)/4.
Решение.
Линейная скорость точек на окружности вала
v1 = ½ ωd.
Линейная скорость точек обоймы
v2 = ½ Ω D.
Так как шарики катятся без проскальзывания, такими же будут и мгновенные скорости тех точек шарика, которые в данный момент соприкасаются с валом и обоймой. Но мгновенную скорость любой точки шарика можно рассматривать как сумму двух скоростей – скорости движения его центра vo и линейной скорости вращательного движения вокруг центра. Вращение шарика будет происходить с некоторой угловой скоростью ωо. Поэтому
v1 = vo - ωоr , v2 = vo + ωоr.
Отсюда
vo = ½ (v1 + v2) = (ωd + Ω D)/4.
В этом выражении каждая из угловых скоростей может быть как положительной, так и отрицательной. При Ω = 0
vo = ωd/4.
4
.
Стержень длиной l = 0.85 м
движется в горизонтальной плоскости.
В некоторый момент времени скорости
концов стержня равны
v1
= 1 м/с и v2 = 1.5 м/с, причем
скорость первого из них направлена под
углом α = 30о к стержню.
Какова угловая скорость ω вращения
стержня вокруг его центра? (МГУ, фак.
ВМК, 2001)
Ответ: ω = 2 рад/с.
Решение.
Поскольку скорости концов стержня в неподвижной системе отсчета различны, он совершает относительно этой системы сложное движение, представляющее собой сумму поступательного и вращательного движений. При этом скорости разных точек стержня различны. Для определения угловой скорости вращения стержня, удобно перейти в систему отсчета, поступательно движущуюся вместе с его центром масс. С этой целью определим скорость центра масс стержня относительно неподвижной системы отсчета.
Если стержень однороден, то центр его масс совпадает с геометрическим центром, радиус- вектор которого определяется как полусумма радиус- векторов его концов:
rc = ½ (r1 + r2).
Дифференцирование этого равенства по времени дает аналогичное соотношение для скорости центра
vc = ½ (v1 + v2).
Согласно закону сложения скоростей скорости концов стержня в системе отсчета, связанной с его центром, выражаются следующим образом
u1 = v1 – vc = ½ (v1 - v2);
u2 = v2 – vc = ½ (v2 – v1).
Из постоянства длины стержня вытекает, что проекции скоростей его концов на направление стержня в каждый момент времени совпадают:
v1 cosα = v2 cosβ.
Поэтому u1 и u2 перпендикулярны стержню, причем
u1 = u2 = ½ ωl.
Следовательно,
ω = |u2 – u1|/l = (v1 sinα + v2 sinβ) /l.
Учитывая, что
cosβ = (v1/v2) cosα,
получаем ответ
ω = [v1 sinα + (v22 – v12 cos2α )1/2]/l = 2 рад/с.
5. При взрыве покоящейся цилиндрической бомбы радиуса R осколки, разлетающиеся в радиальном направлении, за время t удаляются от оси цилиндра на расстояние L1. На какое расстояние L2 от оси цилиндра удаляются осколки за то же время t , если в момент взрыва бомба будет вращаться вокруг своей оси с угловой скоростью ω? Влиянем силы тяжести пренебречь.
Ответ: L2 = [(ωRt)2 + L12]1/2.