Е.М.Елькина

Подготовка школьников к олимпиаде по физике.

I. Кинематика.

ВОПРОСЫ:

1.По какой траектории и как должна двигаться точка, чтобы пройденный ею путь равнялся модулю перемещения?

Ответ. Точка должна двигаться прямолинейно и только в одном направлении.

2.Точка а движется со скоростью 1 м/с, а точка в – со скоростью 2 м/с, причем скорость т. В все время направлена так же, как т. А. Может ли расстояние ав оставаться постоянным?

Ответ. Может. В случае, когда т. А и В движутся по двум концентрическим окружностям.

3. Во время езды на автомобиле снимали показания скорости по спидометру каждый раз, когда она изменялась. Можно ли по этим данным определить среднюю скорость автомобиля?

Ответ. Нельзя, поскольку в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей.

4. Какова (относительно земли) траектория колеблющегося на пружине грузика, помещенного в равномерно движущийся вагон?

Ответ. Синусоида или косинусоида.

5. По какой траектории движется частица в бегущей продольной волне?

Ответ. По отрезку прямой на линии , совпадающей с направлением распространения волны.

6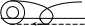 . Существуют ли такие точки движущегося вагона, которые перемещаются не вперед, а назад? Каковы траектории этих точек?

Ответ. Такие точки есть на реборде колеса. Траектория таких точек называется циклоидой.

7. Две материальные точки движутся по окружностям одинакового радиуса с одинаковыми по модулю ускорениями. Ускорение первой точки направлено под углом к касательной, а второй - по радиусу. У какой из этих точек модуль скорости больше?

Ответ. У второй точки центростремительное ускорение больше, значит, больше и модуль скорости.

8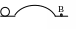 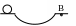. Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и времена движения шариков к моменту их прибытия в точку В? Трением пренебречь.

О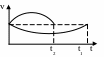 твет. Скорости будут одинаковы. Время движения второго шарика меньше. Примерные графики скорости движения шариков приведены на рисунке. Так как пути, пройденные шариками равны, то, как видно из графика (пути численно равны площадям заштрихованных фигур), t₂ <t₁ .

9. Материальная точка движется по окружности радиусом 3 м. Найти путь и модуль перемещения точки за время, в течение которого радиус-вектор повернулся на 60^о относительно своего первоначального положения. Начало радиус-вектора совпадает с центром окружности.

Ответ. Длина пути L = 2πR(60/360) = π ≈ 3.14 м. Модуль перемещения | s | = R = 3 м.

10. Движение материальной точки описывается уравнениями x = 10cos3t см , y = 10sin3t см. Определить вид траектории и скорость точки. Ответ. Траектория – окружность, скорость точки v = 30 см/с.

11. Движение материальной точки в данной системе отсчета описывается уравнениями x = 2 + t, y = 1 + 2t. Найти уравнение траектории. Построить траекторию на плоскости xOy. Указать положение точки при t = 0, направление и скорость движения.

Ответ. y = 2x – 3, траектория – прямая линия, скорость точки v = √5 м/с.

12. Шарик с высоты H падает на пол, отскакивает без потери скорости и поднимается на ту же высоту. Построить график зависимости ускорения, скорости и перемещения от времени. Начало системы координат расположить на полу, ось х направить вверх.

Р ешение.

В момент удара о пол при t = τ = ( 2H/g)^1/2 в течение короткого промежутка времени возникает значительное ускорение направленное вверх ( на рисунке показано условно). АВ и ВС параболы, А и С вершины парабол.

1 3. Круг радиусом R катится по неподвижному кругу (обкатывает) радиуса 2R. Сколько оборотов совершит малый круг по возвращении в первоначальное положение? Сколько оборотов совершит малый круг при обкатывании внутренней поверхности большого круга?

Ответ: n₁ = 3, n₂ = 1.

Угловая скорость малого круга

ω = v_o/R,

где v_o – скорость центра малого круга. Угловая скорость центра малого круга при его движении вокруг центра большого круга равна

Ω = v_o/(3R).

Значит, когда центр малого круга совершит один оборот вокруг центра большого, сам малый круг совершит три оборота. Аналогично можно показать, что во втором случае малый круг совершит один оборот.

1 4. Тонкая нерастяжимая нить переброшена через блок, и к концу ее привязан груз. Под действием груза цилиндр катится по горизонтальной поверхности без скольжения. Какой путь S пройдет груз, когда цилиндр сделает один полный оборот, если длина окружности

цилиндра L?

Ответ: S = 2L.

Нить размотается на длину, равную L. В свою очередь, цилиндр пройдет путь, также равный L. Поэтому расстояние, которое пройдет груз, равно 2L.

15. С башни по всевозможным направлениям с начальной скоростью v_o , брошены камни. Оказалось, что камень, подлетевший к земле по наиболее пологой траектории, имел при подлете к ней скорость, составляющую с горизонтом угол φ. Определить высоту башни.

Ответ: H = [v_o²/(2g)]tg²φ.

Решение.

Скорость любого камня при подлете к земле

v = (v_o² + 2gH)^1/2 .

Камень, подлетевший по наиболее пологой траектории, имеет наибольшую горизонтальную скорость (v_г)_max. Но

(v_г)_max = v_o .

Поэтому

cos φ = v_o/(v_o² + 2gH)^1/2 .

Отсюда

H = [v_o²/(2g)]tg²φ.