4.Комплекс санның тригонометриялық түрі.

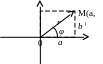z санының a+bi түрінде жазылуында осы санға сәйкес нүктенің декарттық координаттары қолданылады. Жазықтықтағы нүктенің орналасуы оның полярлық координаттарын берілуімен де анықталады: координат басынан нүктеге дейінгі r қашықтығы және абсцисс өсінің оң бағыты мен координат басыан берілген нүктеге дейін жүргізілген радиус векторының арасындағы φ бұрышы.

a + bi « M(a,b)

Анықтама. радиус- векторының ұзындығы комплекс санның модулі деп аталады және r = |z| деп белгілінеді.

r саны – "z C үшін бірмәнді анықталатын, теріс емес нақты сан.

Анықтама. (a,b) радиус векторы мен Ox өсінің оң бағыты арасындағы φ бұрышы комплекс санның аргументі деп аталады және arg z = деп белгіленеді.

φ бұрышы бірмәнді анықталмайды, себебі барлық φ + 2πk (k z) бұрыштары да комплес санның аргументі болып табылады.

Бұрыштың бірмәнділігі үшін оны аралығында алады.

Полярлық және декарттық координаттар арасындағы байланыс.

Егер тікбұрышыты координат жүйесін полярлық жүйемен сәйкестендірсе, онда (1) болады.

Егер компелекс сан нақты болса, онда

Демек, нақты санның модулінің (абсолют шамасының) түсінігі комплекс санның модулінің жалпы түсінігінің дербес жағдайы болып табылады.

(1) формуласын кез келген комплекс санға қолданайық z=a+bi=r(cos +isin ) z санының бұл жазылуы модулінің тригонометриялық түрі деп талады.

Тригонометриялық түрдегі комплекс сандарға қолданылатын амалдар.

а) Комплекс сандарды қосу және азайту операцияларын алгебралық түрде жасауға ыңғайлы, ал көбейту және бөлу операцияларын тригонометриялық түрді пайдаланып жасаған жөн

б) Осы сандарды көбейтейік

(2)

Комплекс сандарды көбейткенде олардың модулдері көбейтіледі, ал аргументтері қосылады.

в) санын санына бөлейік , яғни

⁽³⁾

Бөліндінің модулі бөлінгіштің және бөлгіштің модулдерінің қатынастарына тең, ал бөліндінің аргументі бөлінгіштің және бөлгіштің аргументтерінің айырмасына тең.

Тригонометриялық түрде берілген комплекс сандарды көбейту ережесіне сай: , (4)

Муавр формуласы

Комплекс санды бүтін оң дәрежеге шығарғанда, оның модулі осы дәрежеге шығарылады, ал аргументтері дәреже көрсеткішіне көбейтіледі

n-ші дәрежелі түбірді алу.

Нақты сандарда да сияқты, комплекс санының n-ші дәрежелі түбірі деп Сⁿ = z болатындай С саны аталады. n-ші дәрежелі түбір деп белгілінеді.. Кез келген z комплекс санынан алуға болады, және n мән қабылдайды.

Қорытынды: ,мұндағы (5)

Бірдің түбірлері

Бір санынан n-ші дәрежелі түбір алған жағдай өте маңызды. Бұл түбірдің n мәні бар, және (5) формулалары мен 1= cos0+ isin0 теңдігінен бір санының n-ші дәрежелі барлық түбірлері келесі формуламен беріледі:

(6)

Комплекс жазықтықта бірдің n-ші дәрежелі түбірлері бірлік шеңбердің бойында орналасады және оны тең n доғаларға бөледі. 1- бөлу нүктелерінің бірі, ал нақты емес түбірлер нақты өске қатысты симметриялы орналасқан, яғни жұп-жұптан түйіндес.

Анықтама. e комплекс саны 1 санының n-ші дәрежелі алғашқы түбірі деп аталады (n 1), егер e⁰,e¹,…,e^n-1 жиынтығы zⁿ =1 теңдеуінің барлық шешімдер жиыны болса.

Теорема. z комплекс санының n –ші дәрежелі түбірлерінің барлық мәндерін осы түбірлердің біреуін бірдің n-ші дәрежелі барлық түбірлеріне көбейткенде алуға болады.

Өзін-өзі тексеруге арналған сұрақтар:

1. Комплекс санның түсінігі қалай еңгізіледі?

2. Комплекс санның алгебралық түрі деп не аталады. Нақты және жорамал бөлігі қалай анықталады?

3. Комплекс сандарға қатысты операциялар қалай жүзеге асырылады? Қосу және көбейту операцияларының қандай қасиеттері бар?

4. Алгебралық түрдегі комплекс саннан квадрат түбірді алу формулаларын жаз.

5. Комплекс сандардың бірінші геометриялық интерпретациясының және оларға қолданылатын амалдардың мәні неде?

6. Комплекс сандардың екінші геометриялық интерпретациясының және оларға қолданылатын амалдардың мәні неде?

7. Қандай комплекс сандар түйіндес деп аталады, түйіндес комплекс сандар геометриялық түрде қалай бейнеленеді?

8. Қандай екі комплекс сан тең деп аталады?

9. Жорамал бірлік қалай анықталады?

10. Комплекс санның тригонометриялық түрі қандай координаттарды қолданады?

11.Комплекс санның модулі және аргументі деп не аталады? Олар бірмәнді анықтала ма?

12.Декарттық және полярлық координаттар арасындағы байланысты көрсетіңіз.

13.Комплекс санның тригонометриялық түрі қалай анықталады?

14.Тригонометриялық түрдегі комплекс сандарға операциялар қалай жүргізіледі?

15.Тригонометриялық түрдегі комплекс саннан n-ші дәрежелі түбірді алу формуласын көрсетіңіз. Бірдің барлық n –ші дәрежелі түбірлері қалай табылады?

Әдебиет: 1,110 бет; 2, 8 бет.

№2 дәріс

Тақырып: 2,3-ретті анықтауыштар.

Анықтауыштар қасиеттері

Мақсаты:

Анықтауыштар тұсінігін кіргізу.

2, 3-ретті анықтауыштарды есептеу ережесімен таныстыру.

Қарастыруға арналған сұрақтар тізімі:

1. 2-ші ретті анықтауыш, оны есептеу ережесі.

2. 3-ші ретті анықтауыш, оны есептеу ережесі..

3. Анықтауыштар қасиеттері.

1. 2-ші ретті анықтауыш.

- түріндегі тікбұрышты сандық таблица 2-ші ретті квадрат матрица аталады.

а_11, а₁₂,…- матрица элементтері.

а₁₁а₂₂-а₂₁а₁₂ саны 2-ші ретті анықтауыш аталады және Диагональ символымен белгіленеді. Сонымен = а₁₁а₂₂-а₂₁а₁₂.(1)

Анықтауыштың а_11,а₂₂ сандары орналасатын диагоналі бас диагонал аталады, екінші диагоналі- қосымша диагонал.

Екінші ретті анықтауышты есептеу ұшын оның бас диагонал бойындағы элементтерінің көбейтіндісімен қосымша диагонал бойындағы элементтерінің көбейтіндісінің айырымын табу керек.

Мысал

1 = анықтауышты есептеу керек.

Шешімі.

(1) формуласын қолданып, табамыз = 5*3-(-20*15 = 15+30 = 45.

2. 3-ші ретті анықтауыш.

Анықтама..Үшінші ретті анықтауыш деп, келесі формула бойынша есептелетін сан аталады:

(2)

Саррюс ережесі немесе үшбұрыш әдісі:

Әр қайсысы матрицаның кез келген жолынан және кез келген бағанынан алынған үш санның көбейтіндісі болатын алты мүшенің алгебралық қосындысын аламыз.

2.Мысал. Келесі анықтауышты есетейік: =

Шешімі. Саррюс ережесін қолданып (2) деп белгіленген көбейтінділерді есептейміз:

1: 1*(-1)*(-2)=2; 4*(-7)*3=-84; 2*5*6=60.

2: 6*(-1)*3=-18; 4*2*(-2)=-16; (-7)*5*1=-35.

Соңғы кобейтінділер (2)- ге теріс таңбамен жазылады. Сонымен

= = 2-84+60+18+16+35 = 47.

Үшбұрыш әдісін меңгергендерге ескерту. (2)-ге кіретін көбейтінділерді бөлек есептеу қажеті жоқ. Бәрінде бір жолға жазып, тек қана таңбасын ескере отырып есептеуге болады.