9.3. Пружинный маятник

Пусть груз массой m, лежащий на идеально гладкой горизонтальной плоскости, прикреплён к пружине жёсткостью k, которая другим концом закреплена на стенке (рис. 9.2, а). Очевидно, что если шарик вывести из положения равновесия и отпустить, то он будет совершать колебания. Поэтому такая колебательная система называется пружинным маятником. Покажем, что колебания груза в этом случае будут описываться уравнением (9.1).

Проведём ось х как показано на рис 9.2, а, приняв х = 0 в точке равновесия груза. Выведем груз из равновесия, сдвинув его на небольшое расстояние х вправо, и затем отпустим. По закону Гука, на груз при этом будет действовать упругая сила F_x = −kx, направленная против смещения (рис. 9.2, б). Тогда, в силу 2-го закона Ньютона, уравнение движения груза будет таким:

m a_x = −kx,

или:

,

или

, (9.4)

где символом ω² обозначено отношение k/m, т. е.

ω = . (9.5)

Видно, что уравнение движения груза (9.4) полностью совпадает с (9.1), следовательно, груз совершает синусоидальные колебания с угловой частотой (9.5). В общем виде эти колебания описываются функцией (9.3), в которой коэффициенты А и В определяются из начальных условий, т. е. из способа возбуждения колебаний груза. Начальными условиями для уравнения (9.4) являются значения координаты и скорости груза в начальный момент времени: х(0) и (0) = υ(0). Рассмотрим два типичных способа возбуждения колебаний груза: 1) груз оттянули и отпустили; 2) груз толкнули из положения равновесия.

Вариант 1: груз оттянули вправо на заданное расстояние Х и отпустили. Тогда начальные условия запишутся так:

х(0) = Х, υ(0) = (0) = 0.

Подставляя (9.3) в первое начальное условие, получаем:

А sin 0 + B cos 0 = Х,

откуда В = Х (коэффициент А пока не определён).

Подставляя (9.3) во второе начальное условие, получаем:

= Аω cos 0 – Bω sin 0 = Аω = 0,

о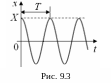 ткуда А = 0. Таким образом, при данном способе возбуждения закон колебаний груза будет иметь вид (рис. 9.3):

х = Х cos ωt. (9.6)

Вариант 2: груз толкнули из положения равновесия, т. е. в момент t = 0 при х = 0 ему сообщили начальную скорость υ₀. В этом случае начальные условия будут иметь вид:

х(0) = 0, υ(0) = (0) = υ₀.

Подставляя (9.3) в первое начальное условие, получаем:

0 = А sin 0 + B cos 0,

откуда В = 0, т. е. теперь можно записать:

х = А sin ωt.

Подставляя это выражение во второе начальное условие, получаем:

υ₀ = Аω cos 0,

т. е. А = υ₀ /ω. И тогда при данном способе возбуждения закон колебаний груза будет иметь вид (рис. 9.1):

х = Х sin ωt, (9.7)

где − амплитуда колебаний.

В обоих вариантах частота колебаний одна и та же (формула 9.5), и она определяется только массой груза и жёсткостью пружины. Период колебаний

.

ПРИЛОЖЕНИЕ: закон Гука и энергия сжатой (растянутой) пружины.

Закон Гука утверждает, что для сжатия или растяжения пружины на величину х, к ней надо приложить силу F, пропорциональную х: F= kx. Коэффициент пропорциональности k называется жёсткостью пружины. Если к пружине прикреплено какое-то тело (груз), то на него со стороны деформированной пружины будет действовать сила, пропорциональная деформации х и противоположно направленная этой деформации: F_х = −kx (рис. 9.2,б).

Растягивая или сжимая пружину, сила F совершает работу

А = ,

в результате которой пружина приобретает потенциальную энергию

W = .