2.2. Использование неравенства Чебышева для оценки риска

Как уже отмечалось, математическое ожидание и дисперсия являются двумя показателями, определяющими степень риска, но если воспользоваться неравенством Чебышева, можно получить один показатель (вероятность нежелательного события), зависящий от этих двух даже в том случае, когда неизвестен закон распределения случайной величины.

Неравенство Чебышева. Если случайная величина Х имеет конечную дисперсию и математическое ожидание m_x, то вероятность Р того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине будет меньше любого положительного числа  > 0, определяется неравенством

. (2.18)

Вторая форма неравенства Чебышева имеет вид

. (2.19)

Пусть инвестиции осуществляются за счет кредита, взятого под залог недвижимости под процентную ставку r_k. Оценим риск того, что инвестор не сможет вернуть свой долг и потеряет недвижимость (риск банкротства).

В данном случае риск R будет оцениваться вероятностью Р нежелательного события, что ожидаемая доходность инвестиций Х окажется меньше r_k:

X < r_k. (2.20)

Неравенство (2.20) можно записать в следующем виде:

. (2.21)

Тогда вероятность события

. (2.22)

Используя неравенство Чебышева и обозначая , получаем

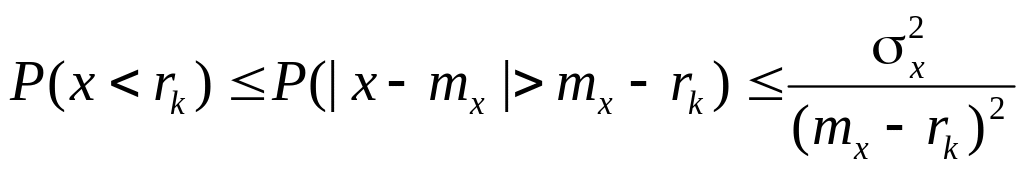. (2.23)

Таким образом, степень риска

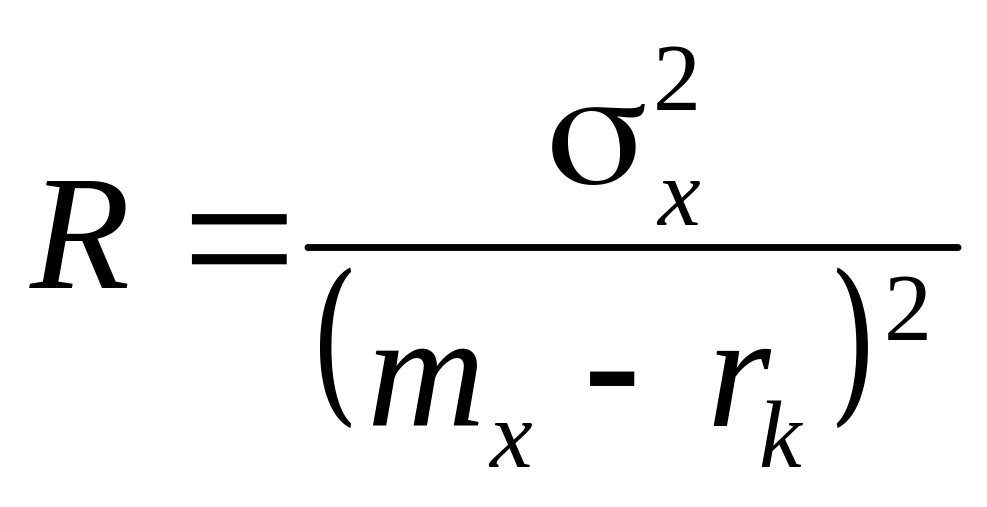. (2.24)

Если, например, инвестор хочет, чтобы риск банкротства был не больше, чем , то для этого необходимо выполнить условие

или

(2.25)

Во многих случаях допустимый риск имеет меньшую величину, например р_доп = 0,001.

В этом случае

,

или

.

Пример. Предприниматель берет кредит под 10% годовых для реализации инновационного проекта. При этом эксперты оценивают, что риск (среднее квадратическое отклонение), связанный с колебанием ожидаемой доходности проекта , равен 5%. Необходимо оценить уровень ожидаемого доходности , чтобы избежать банкротства с вероятностью .

Решение. Имеем . Используем формулу (2.25), получаем

,

т.е. уровень ожидаемой доходности должен быть не меньше, чем 25%.

Рассмотрим еще одну ситуацию, когда инвестор вкладывает в обычные акции лишь часть своего капитала, оставляя некоторую часть на сохранность под практически безрисковую процентную ставку наращивания . Какая будет при этом величина риска (вероятность банкротства)?

Пусть А – капитал инвестора, тогда х₀ А – часть, которая вкладывается в практически безрисковый актив с процентной ставкой .

Очевидно, что банкротство будет в случае, когда

, (2.26)

где – процентная ставка обычных акций (очевидно, что для банкротства должна быть отрицательной).

Из выражения (2.26), получаем, что банкротство будет в том случае, когда

. (2.27)

Используя неравенство Чебышева, определим уровень ожидаемого дохода от обычных акций, при котором вероятность банкротства будет меньше . Считая, что есть случайная величина Х, имеем:

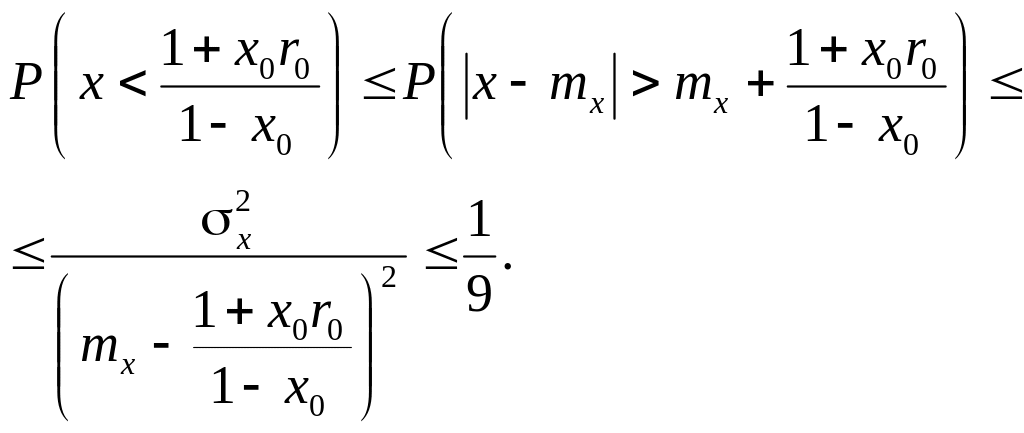
Отсюда

. (2.28)

Сравнивая выражение (2.28) и (2.25), видим, что игра на бирже на собственный капитал существенно менее рискованна. Даже если вложить весь собственный капитал в обычные акции (х₀ = 0), то уровень ожидаемой доходности от акций, позволяющий избежать банкротства с вероятностью , должен быть не меньше

. (2.29)

Пример. Инвестор вкладывает половину своего капитала в безрисковые ценные бумаги, доходность от которых составляет 30%. Вторую половину денег он собирается вложить в рискованный проект. Среднеквадратичное отклонение доходности от этого проекта равно 100(%.) Инвестор хотел бы, чтобы вероятность банкротства была бы для него не больше . Какой для этого должна быть ожидаемая доходность от инвестиций?

Решение. Используя выражение (2.28), получаем

.

Следовательно, ожидаемая доходность от инвестиций должна быть не менее 70%.

Пример. При производстве товаров на экспорт, производитель хотел бы, чтобы риск банкротства был бы не больше . В производстве вкладывают весь собственный капитал. Ожидаемый уровень доходности составляет 10%.

Определить, каким должно быть среднеквадратичное отклонение доходности .

Решение. Дано: х₀ = 0, .

В соответствии с выражением (2.28) имеем

.

Таким образом, среднеквадратичное отклонение должно быть не больше, чем 36,7%.

Неравенство Чебышева дает более грубую оценку риска по сравнению с той, которую получают по известному закону распределения случайной величины Х, характеризующей доходность.