5.7. Другие методы решения многокритериальной задачи

5.7.1. Оптимизация доминирующего частного критерия при ограничениях на значения доминируемых критериев

Пусть среди частных критериев f_i(x), критерий f₁(x) является доминирующим (рассматриваем случай, когда все критерии подлежат минимизации). Тогда многокритериальную задачу сводят к однокритериальной:

для х, удовлетворяющих ограничениям:

,

где q_i  допустимое (пороговое) значение i-го критерия.

5.7.2. Метод последовательных уступок

Метод последовательных уступок решения многокритериальных задач применяется в случае, когда частные критерии могут быть упорядочены в порядке убывающей важности, и заключается в следующем.

Пусть нумерация критериев соответствует их важности, т.е. f₁(x)  наиболее важный критерий, f_n(x) - наименее важный.

На первом шаге решается задача оптимизации по критерию f₁(x):

. (5.27)

Пусть f₁^  минимальное значение критерия в задаче (5.27). Далее назначается, исходя из практических соображений и принятой точности, некоторая уступка , которую субъект риска согласен допустить в f₁(x). Тогда на втором шаге ищется решение, минимизирующее f₂(x), при ограничении, что , т.е. решается задача

(5.28)

На k-м шаге решается задача

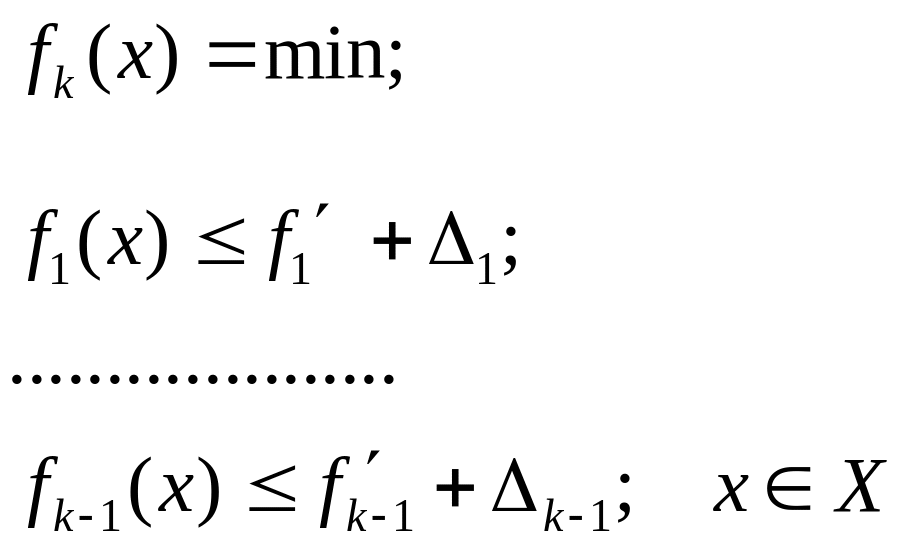
и т.д. до n-го шага. Этот метод, однако, может и не привести к эффективному решению.

В заключение отметим, что выбор критерия свертки частных критериев в задаче многокритериальной оптимизации чаще всего является не математической задачей и в каждой конкретной ситуации решается по-своему. Окончательное решение лучше принимать путем решения задач по различным обобщенным критериям, на основе анализа устойчивости и чувствительности к изменению критериев и исходных данных.

6. Принятие решений на основе нечёткой информации

Пойди туда – не знаю куда!

Принеси то – не знаю что!

Русская народная сказка

6.1. Неопределённость и неточность

Единичность реализации проектов, а следовательно, невозможность иметь презентабельную и однородную статистику для принятия решений вынуждает искать не стохастические методы представления неполноты информации, необходимой для прогнозирования исхода (результата) решения. Кроме того, сама природа неполноты (недостаточности) информации часто не является стохастической, что особенно присуще коммерческим проектам. Например, влияние макрополитических процессов на налоговое законодательство носит совершенно не стохастический характер, но недостаточная информативность в возможных изменениях налоговых законов может привести к краху коммерческого проекта.

Недостаточность (неполнота) информации у ЛПР имеет две стороны: неопределённость и неточность.

Степень неопределённости информации задаётся, например, с помощью квалификаторов “возможно”, “навер­няка”, “вероятно”, “может быть” и др.. Причём квалификатор “вероятно” может носить как стохастический характер, так и характер субъективного суждения (эпистомологический).

Неточность определяется границами (размерами) задания информационного множества. Примером неточного высказывания является “Данный проект даст доходность не менее 5%”. А такое высказывание: “Вероятно, что данный проект даст большую доходность”, содержит неопределённость, характеризующуюся словам – “вероятно” и неточность информации, словом – “большую”.

Очевидно, что между неопределённостью и неточностью существует противоречие, которое выражается в том, что с повышением точности информации возрастает ёё неопределённость. И, наоборот, уменьшение неопределённости приводит в общем случае к увеличению неточности информации.

Хотя в стохастических моделях объектов риска также имеется неопределённость и неточность, но эти модели требуют обработки точной, но распределённой по реализациям информации. Как только возникает неточность в оценке отдельных реализаций, стохастическая модель становится неприемлемой.

Наступивший век – век искусственного интеллекта и экспертных систем, в которых используются такие неопределённые и неточные понятия, как и в рассуждениях человека. Такие системы оперируют нечёткими понятиями, для описания которых создана теория нечётких множеств (fuzzy sets). Эта теория, основоположником которой является Лотфи Заде (Lotfi Zadeh), позволяет описывать неточную и неопределённую информацию с помощью нечётких множеств, а также оперировать этими множествами.

В настоящее время нечёткие системами принятия решений используются в промышленных роботах, в системах автоматического распознавания речи и изображений, в системах управления поездами метро и бытовыми приборами и других областях.

Нечёткое моделирование более естественно описывает характер человеческого мышления, чем традиционное формально-логическое моделирование, и позволяет получать лучшие результаты в системах управления с неполной информацией, что и обуславливает перспективность применения его в теории принятия управленческих решений [1, 3, 24].