1. Риск в менеджменте, основные принципы его анализа

1. Понятие риска и задача принятия решений

Кто не рискует, тот не выигрывает.

Народная мудрость

Этимология слова “риск” (от староитальянского “risi­care”, означающего “отважиться”) показывает, что риск связан с задачей принятия решений. Французское “risqué”, происходящее из итальянского языка, уже означает “опасность”.

Таким образом, риск – это опасность получения нежелательного результата при реализации выбранного решения.

В литературе встречаются различные понимания термина “риск” и в него иногда вкладывают довольно сильно отличающееся друг от друга содержание. Однако общим во всех этих представлениях является то, что риск связан с возможностью того, что произойдет нежелательное событие, возникнет неблагоприятное состояние и т.д. В частном случае риск понимается как вероятность недостижения поставленной цели.

Характерными чертами риска являются:

• риск присущ любому решению, результаты которого будут известны только в будущем;

• полное устранение риска невозможно, поскольку будущее можно лишь прогнозировать, а точно описать невозможно;

• даже непринятие решения уже содержит в себе риск упущенной возможности.

Саму задачу принятия решений в условиях риска можно представить в виде системы, состоящей из трёх подсистем (рис. 1.1):

1) объекта риска, или объекта управления;

2) субъекта риска – лица, принимающего решение (ЛПР), или управляющей подсистемы;

3) среды, в которой функционируют объект и субъект риска.

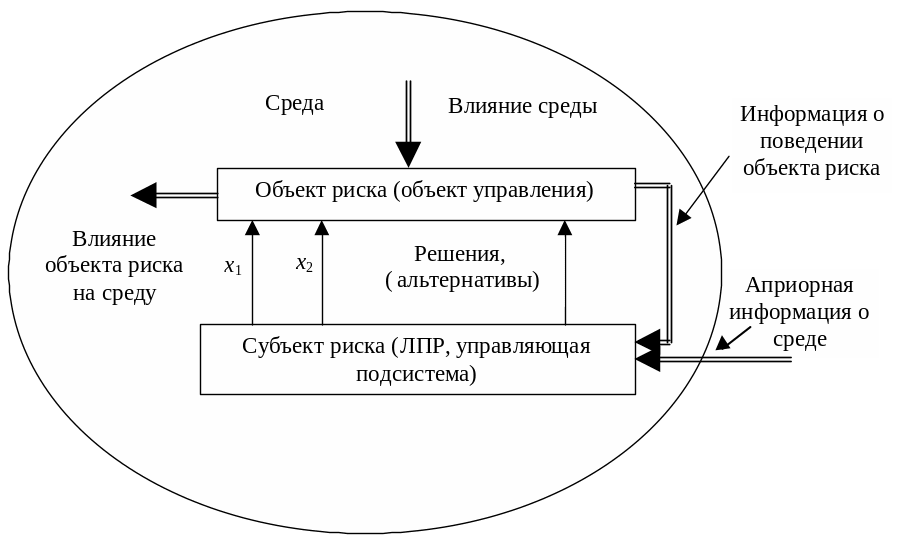
Рис. 1.1. Системное описание задачи принятия решений в условиях риска

Объектом риска является экономическая система, эффективность и условия функционирования которой в будущем точно не известны.

Под субъектом риска понимается принимающее решение лицо (индивид или коллективный орган), которое заинтересовано в результатах управления и имеет компетенцию принятия решения относительно объекта риска.

Источник риска – это факторы (явления, процессы), которые вызывают неопределенность результатов решения.

Состояние объекта риска (объекта управления) зависит от выбранного решения х_i при , принадлежащего множеству допустимых решений Х ( ), и состояния среды s_j, принадлежащего множеству возможных состояний S. Принципиальным является то обстоятельство, что ЛПР не может непосредственно воздействовать на среду и, как правило, не имеет точной информации о её состоянии. Но опосредованное (через объект риска) воздействие на среду в некоторых случаях может и осуществляться.

Для выбора оптимального решения каждая ситуация (х_i, s_j) оценивается по одному или нескольким показателям (критериям) f_k (х_i, s_j ), . Таким образом, получается трёхмерная оценочная матрица исходов (результатов принятых решений) (рис. 1.2)

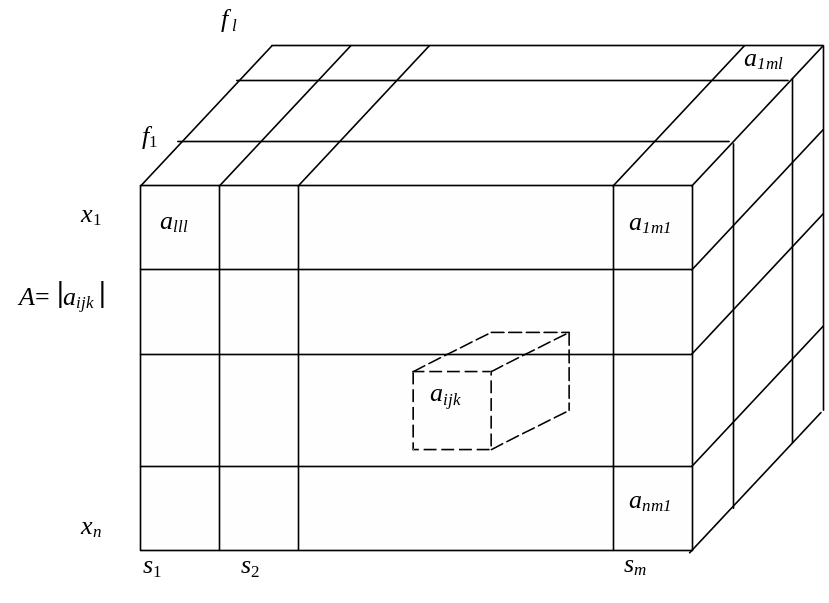
Рис. 1.2. Трёхмерная оценочная матрица исходов

Элемент а_ijk матрицы А даёт оценку решения x_i в условиях состояния среды s_j по показателю (критерию) f_k. Выбор множества возможных вариантов решений Х, определение множества возможных состояний среды S и критериев f_k, является скорее „искусством”, нежели наукой, а вот методы нахождения оптимального решения составляют ту часть научной задачи, которая будет рассмотрена ниже.

Общий алгоритм принятия решения представлен на рис. 1.3.

Рис. 1.3 Общий алгоритм принятия решений

Задачи принятия решений в условиях риска можно классифицировать следующим образом:

• в зависимости от числа частных показателей различают однокритериальные и многокритериальные задачи принятия решений;

• в зависимости от вида описания неполноты (неопределённости) информации, которая используется для принятия решений, различают задачи принятия решений при стохастической исходной информации (часто этот случай и называют принятием решения в условиях риска) и принятия решений при нечёткой исходной информации;

• в зависимости от модели состояния среды различают задачи принятия решений при:

• известном состоянии среды;

• состоянии среды, описываемом случайными величинами;

• неопределённости состояний среды;

• игровой модели, когда состояние среды определяет конкурирующая сторона.