3.3.7. Решение игр 2n и m2

Как уже отмечалось в теореме об активных стратегиях, любая конечная игра mn имеет решение, в котором число активных стратегий каждого игрока не превосходит , где . Следовательно, у игры 2n или m2 всегда имеется оптимальное решение содержащее не более двух активных стратегий у каждого из игроков  . Если эти активные стратегии игроков будут найдены, то игры 2n и m2 превращаются в игры 22, методы решения которых рассмотрены выше.

Практически решение игры 2n осуществляется следующим образом:

1) строится графическое изображение игры для игрока А;

2) выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы (максимин), которая равна цене игры ;

3) определяется пара стратегий игрока В, пересекающихся в точке оптимума. Эти стратегии и являются активными стратегиями игрока В.

Таким образом, игра 2n сведена к игре 22, которую более точно можно решить алгебраическим методом.

Если в точке оптимума пересекается более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них.

Решение игры m2 осуществляется аналогично. Но в этом случае строится графическое изображение игры для игрока В и выделяется не нижняя, а верхняя граница выигрыша (так как находится оптимальная смешанная стратегия игрока В), и на ней находится точка оптимума с наименьшей ординатой (минимакс).

Пример. Найти решение игры, платёжная матрица которой имеет вид:

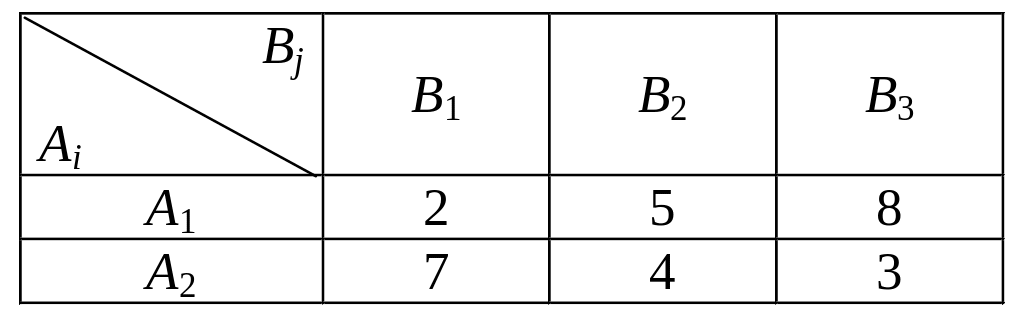
Платёжная матрица не имеет седловой точки, поэтому оптимальное решение должно быть в смешанных стратегиях. Строим графическое изображение игры для игрока А (рис.3.11).

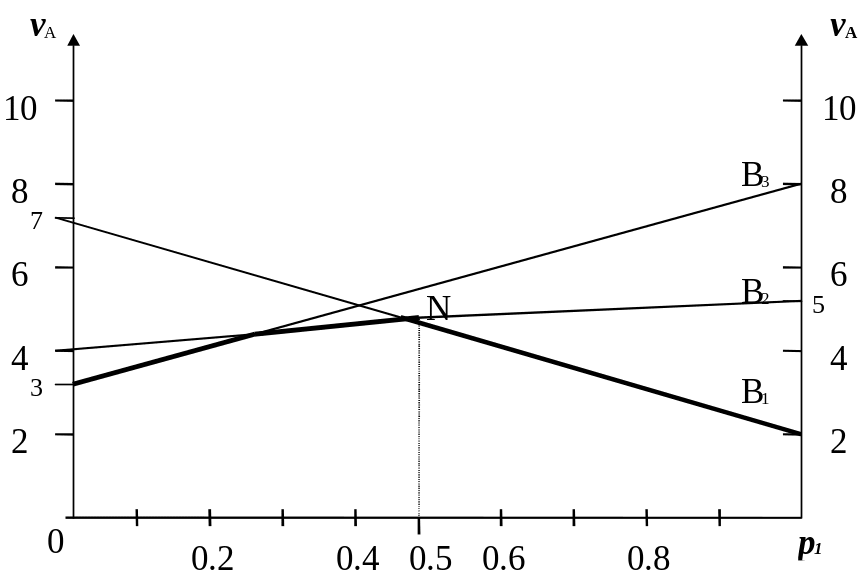
Рис. 3.11. Графическое изображение игры для игрока А

Точка N (максимин) является точкой оптимума. В этой точке пересекаются линии, соответствующие активным стратегиям B₁ и B₂ игрока B.

Таким образом, исключая стратегию B₃, получаем матричную игру 2x2 с платёжной матрицей вида

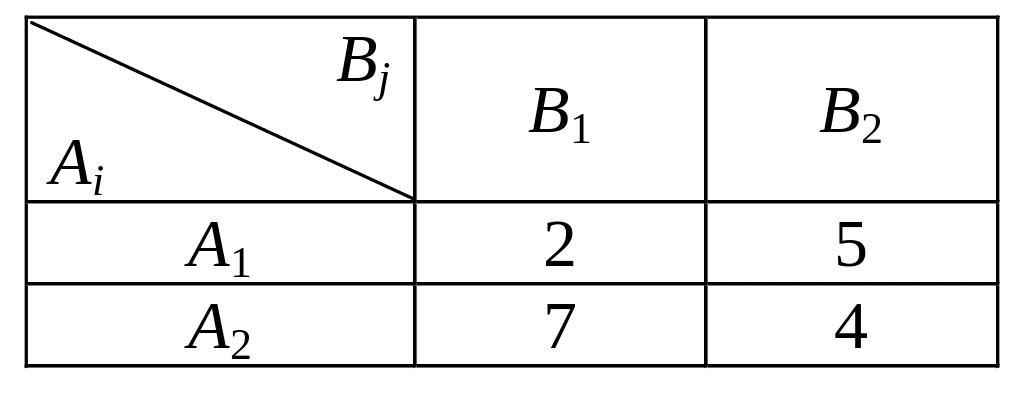
Используя алгебраический метод решения этой игры, получаем точное решение

; ;

; ;

.

Ответ: ; ; .

Пример. Найти решение игры, платёжная матрица которой имеет вид

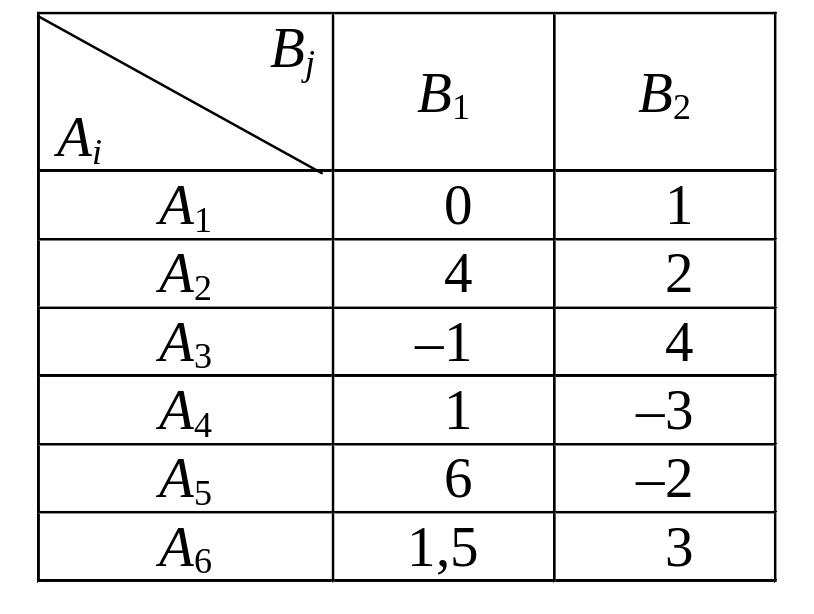
Платёжная матрица не имеет седловой точки. Для сведения данной игры к игре 22 строим её графическое изображение для игрока В (рис. 3.12).

Рис.3.12. Графическое изображение игры для игрока В

Точка М (минимакс) является точкой оптимума. В этой точке пересекаются отрезки, соответствующие активным стратегиям А₂, А₆ и А₃ игрока А. Таким образом, исключая стратегии А₁, А₄ и А₅ и выбирая из трех активных стратегий две (например, А₂ и А₃ или А₂ и А₆), приходим к матричной игре 22. Выбор стратегий А₃ и А₆ исключен, так как в этом случае точка М перестанет быть точкой минимакса.

Пусть выбираются стратегии А₂ и А₃. Тогда игра 22 приобретает вид

Оптимальные смешанные стратегии данной игры, а, следовательно, и исходной игры определяются следующими вероятностями:

; ;

; ;

.

Ответ: ; ; .

Другой вариант игры 22 получается, если использовать стратегии А₂ и А₆. В этом случае платёжная матрица имеет вид

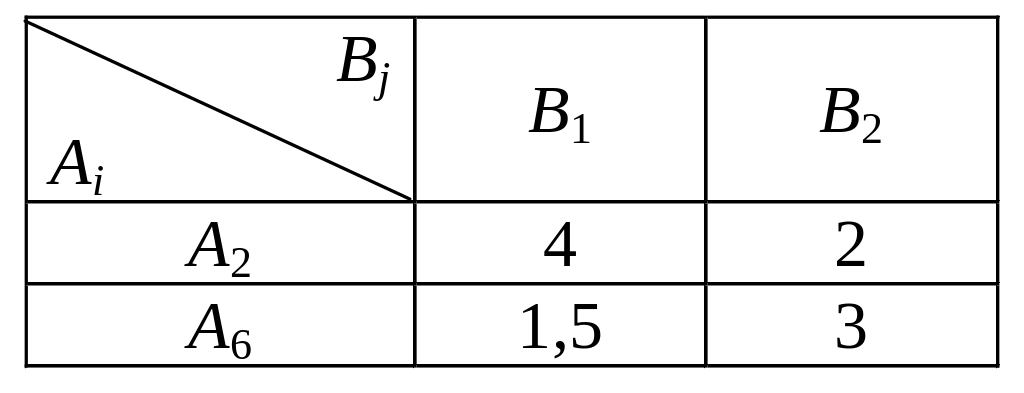
Тогда

; ;

; ;

.

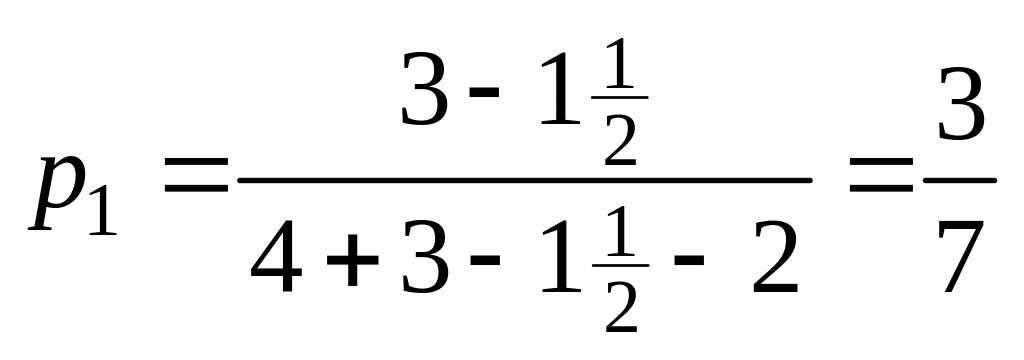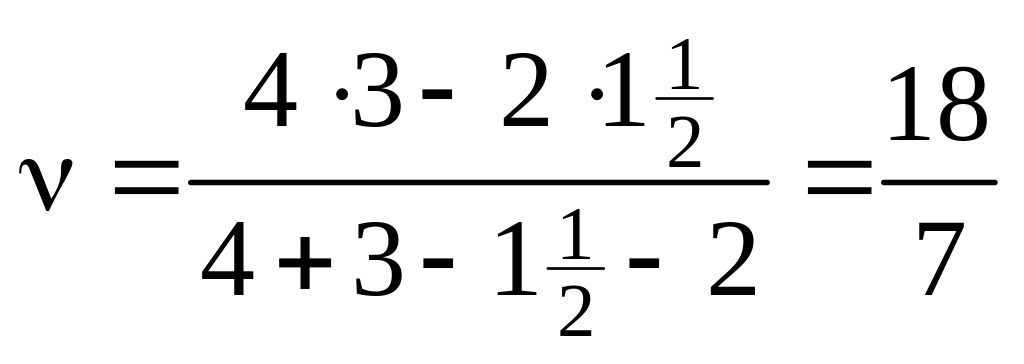Ответ: ; ; .

Естественно, что цена игры для обоих способов решения задачи одинакова.

В заключение наметим общую схему решения матричных игр 2n и m2:

1. Определяется наличие седловой точки, т.е. возможность решения игры в чистых стратегиях. Если нижняя цена игры  не равна верхней цене игры , то осуществляется поиск решения в смешанных стратегиях.

2. Производится упрощение матричной игры путем исключения дублирующих и доминируемых стратегий. Если упрощенная игра имеет размерность не 22, то переходим к этапу 3.

3. Строится графическое изображение игры и определяется две активные стратегии игрока, имевшего в исходной задаче число стратегий больше двух.

4. Решается матричная игра 22.