
- •Содержание
- •Автокорреляция случайного возмущения. Причины. Последствия.
- •Алгоритм проверки адекватности парной регрессионной модели.
- •Алгоритм проверки значимости регрессора в парной регрессионной модели
- •4. Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.
- •5. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений.
- •6.Гетероскедастичность случайного возмущения. Причины.
- •7.Динамическая модель из одновременных линейных уравнений (привести пример)
- •8.Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие.
- •Необходимое условие идентифицируемости
- •9. Индивидуальная оценка значения зависимой переменной
- •10. Интервальная оценка индивидуального значения зависимой переменной
- •11.Классическая парная регрессионная модель. Спецификация модели.
- •12.Коэффициент детерминации в регрессионной модели.
- •13.Ковариация, коэффициент корреляции и индекс детерминации.
- •14.Количественные характеристики взаимосвязи пары случайных переменных
- •15.Коэффициент корреляции и индекс детерминации.
- •16.Линейная модель множественной регрессии
- •17.Метод наименьших квадратов: алгоритм метода; условия применения
- •18.Метод показателей информационной ёмкости
- •19.Методы подбора переменных в модели множественной регрессии
- •20.Методы сглаживания временного ряда.
- •21, 52. Модели временных рядов
- •22.Модели с бинарными фиктивными переменными
- •23.Модели с частичной корректировкой
- •24.Настройка модели с системой одновременных уравнений.
- •25, 26. Нелинейная модель множественной регрессии Кобба-Дугласа. Оценка её коэффициентов
- •27.Нормальный закон распределения как характеристика случайной переменной
- •28.Обобщённый метод наименьших квадратов
- •29, 30. Ожидаемое значение случайной переменной, её дисперсия и среднее квадратическое отклонение
- •31. Определение соответствия распределения случайных возмущений нормальному закону распределения
- •32. Основные числовые характеристики вектора остатков в классической множественной регрессионной модели.
- •33.Отражение в модели влияния неучтённых факторов
- •34.Отражение в эконометрических моделях фактора времени
- •35, 36, 45.Оценивание линейной модели множественной регрессии в Excel
- •37.Оценивание регрессионной модели с фиктивной переменной наклона
- •38.Оценка коэффициентов модели Самуэльсона-Хикса
- •39. Оценка параметров множественной регрессионной модели методом наименьших квадратов
- •40. Оценка параметров парной регрессионной модели методом наименьших квадратов
- •41. Оценка статистической значимости коэффициентов модели множественной регрессии.
- •Ситуации
- •42. Подбор переменных в модели множественной регрессии на основе метода оценки информационной ёмкости.
- •43. Подбор переменных в модели множественной регрессии методом «снизу вверх»
- •44. Подбор переменных в модели множественной регрессии методом исключения переменных («сверху вниз»).
- •46. Последствия гетероскедастичности. Тест gq
- •47. Применение теста Стьюдента в процедуре подбора переменных в модели множественной регрессии
- •48. Применение фиктивных переменных при исследовании сезонных колебаний: спецификация модели, экономический смысл параметров при фиктивных переменных
- •49. Принципы спецификации эконометрических моделей и их формы
- •50. Проблема мультиколлинеарности в моделях множественной регрессии. Признаки мультиколлинеарности
- •51. Прогнозирование экономических переменных. Проверка адекватности модели
- •53.Регрессионные модели с фиктивными переменными.
- •54.Свойства временных рядов
- •55.Составление спецификации модели временного ряда.
- •56, 57. Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам.
- •58.Спецификация моделей со случайными возмущениями и преобразование их к системе нормальных уравнений.
- •59.Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов.
- •60.Статистические свойства оценок параметров парной регрессионной модели
- •61.Статистические характеристики выборки и генеральной совокупности статистических данных. Их соотношения.
- •62.Схема Гаусса – Маркова
- •63.Теорема Гаусса-Маркова
- •64. Тест ошибочной спецификации Рамсея.
- •Тест Стьюдента
- •66, 67. Типы переменных в эконометрических моделях. Структурная и приведённая формы спецификации эконометрических моделей.
- •68. Устранение автокорреляции в парной регрессии
- •69. F-тест качества спецификации множественной регрессионной модели.
- •70. Фиктивная переменная наклона: назначение; спецификация
- •71.Функция регрессии как оптимальный прогноз
- •72.Характеристики сервиса «Описательная статистика».
- •73. Метод наибольшего прадоподобия
- •Последовательность решения:
- •74. Что такое стационарный процесс
- •75. Эконометрика, её задача и метод.
- •76.Экспоненциальное сглаживание временного ряда
- •77. Этапы построения эконометрических моделей
- •78. Этапы решения экономико-математических задач.
8.Идентификация отдельных уравнений системы одновременных уравнений: порядковое условие.
Коэффициент уравнения называется идентифицируемым, если его можно вычислить на основе приведенных коэффициентов, причем точно идентифицируемым, если он единственный, и сверхидентифицируемым, если он имеет несколько разных оценок. В противном случае он называется неидентифицируемым.
Какое-либо структурное уравнение является идентифицируемым, если идентифицируемы все его коэффициенты. Если хотя бы один структурный коэффициент неидентифицируем, то и все уравнение является неидентифицируемым.
Модель считается идентифицируемой, если каждое ее уравнение идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель неидентифицируема. Уравнение структурной модели может быть идентифицируемо, если выполняется порядковое условие.
Общий вид каждого
уравнения модели в структурной форме
можно записать как: (2.4) 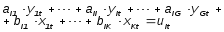
где: G – количество эндогенных переменных в модели
K – количество предопределенных переменных в модели
Необходимое условие идентифицируемости
Теорема 1. Пусть i-ое поведенческое уравнение модели (2.4) идентифицируемо. Тогда справедливо неравенство
Mi (пред) G – Mi (энд) – 1. (2.5)
В нём: Mi (пред) – количество предопределённых переменных модели, не включённых в i-ое уравнение;
Mi (энд) – количество эндогенных переменных модели, не включённых в i-ое уравнение.
Замечание. Справедливость неравенства (2.5) является необходимым условием идентифицируемости i-го уравнения. Это значит, что, когда неравенство (2.5) несправедливо, то i-ое уравнение заведомо неидентифицируемо. Однако при выполнении неравенства (2.5) ещё нельзя сделать вывод о идентифицируемости данного уравнения
Условие (2.5), именуемое правилом порядка, позволяет выявлять неидентифицируемые уравнения модели, но не даёт возможности отмечать её идентифицируемые уравнения
Определение неидентифицируемых уравнений производится методом «от противного»: если условие (2.5) не выполняется для i-го уравнения, то оно неидентифицируемо.
9. Индивидуальная оценка значения зависимой переменной
Для определения границ доверительного интервала для отдельных (индивидуальных) значений зависимой переменной, применяя стандартную процедуру, составляем дробь Стьюдента:
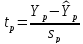 ,
числитель дроби – ошибка прогноза
индивидуального значения эндогенной
переменной (ер),
знаменатель – оценка СКО (среднего
квадратического отклонения) ошибки
прогноза.
,
числитель дроби – ошибка прогноза
индивидуального значения эндогенной
переменной (ер),
знаменатель – оценка СКО (среднего
квадратического отклонения) ошибки
прогноза.
Выразим дисперсию данной ошибки через выборочные данные:
 где учтено, что
где учтено, что
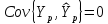 на интервале прогнозирования. Заменяя
значение дисперсии
на интервале прогнозирования. Заменяя
значение дисперсии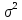 его
оценкой, получим выражение для оценки
дисперсии прогноза наблюденияt=p
его
оценкой, получим выражение для оценки
дисперсии прогноза наблюденияt=p
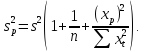
Границы доверительного
интервала прогноза индивидуальных
значений Yt
определяют
по ф-ле:
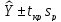
Согласно t-критерию Стьюдента, выдвигается «нулевая» гипотеза H0 о статистической незначимости коэффициента уравнения регрессии (т. е. о статистически незначимом отличии величины а или bi от нуля). Эта гипотеза отвергается при выполнении условия t > tкрит, где tкрит определяется по таблицам число1 (p pt-критерия Стьюдента (П2) по числу степеней свободы k1 = n независимых переменных в уравнении регрессии) и заданному уровню значимости α.
t-критерий Стьюдента применяется в процедуре принятия решения о целесообразности включения фактора в модель. Если коэффициент при факторе в уравнении регрессии оказывается незначимым, то включать данный фактор в модель не рекомендуется.
