4. Алгоритм теста Голдфелда-Квандта на наличие (отсутствие) гетероскедастичности случайных возмущений.

Гипотеза(1):

Шаг 1. Уравнения наблюдений объекта следует упорядочить по возрастанию суммы модулей значений предопределенных переменных модели (2),

т.е. по возрастанию значений

Шаг 2. По первым упорядоченным уравнениям наблюдений объекта вычислить МНК-оценки параметров модели и величинугде- МНК-оценка случайного возмущения

Шаг 3. По последним упорядоченным уравнениям наблюдений вычислить МНК-оценки параметров модели и величинуESS, которую обозначим

Шаг 4. Вычислить статистику .

Шаг 5. Задаться уровнем значимости и с помощью функцииFРАСПОБР Excel при количествах степеней свободы , гдеопределить (1--квантиль,распределения Фишера.

Шаг 6. Принять гипотезу (1), если справедливы неравенства

Т.е. при справедливых неравенствах случайный остаток в модели (2) полагать гомоскедастичными. В противном случае гипотезу (1) отклонить как противоречащую реальным данным и сделать вывод о гетероскедастичности случайного остатка в модели (2).

5. Алгоритм теста Дарбина-Уотсона на наличие (отсутствие) автокорреляции случайных возмущений.

Гипотеза (1):

Шаг 1. По уравнениям наблюдений объекта 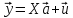следует вычислить МНК-оценки и оценки случайных остатков.

Шаг 2. Вычислить величину

Шаг 3. Из таблицы, составленной Дарбиным и Уотсоном, по количеству n уравнений наблюдений и количеству k объясняющих переменных следует выбрать две величины

Шаг 4. Проверить, в какое из пяти подмножеств интервала (0,4) попала величинаDW. Сделать вывод о присутствии/отсутствии автокорреляции.

Если попало в -, то автокорреляция присутствует

Если попало в +, то автокорреляция отсутствует

Если попало в ///, то зона неопределенности.

6.Гетероскедастичность случайного возмущения. Причины.

Гетероскедастичность - ситуация, когда дисперсия ошибки в уравнении регрессии изменяется от наблюдения к наблюдению. В этом случае приходится подвергать определенной модификации МНК (иначе возможны ошибочные выводы). Для обнаружения гетероскедастичности обычно используют 3 теста: тест ранговой корреляции Спирмена, тест Голдфеда - Квандта и тест Глейзера Доугерти.

Гетероскедастичность случайных возмущений – возмущения обладают различными дисперсиями r²_i=r²w_i, но не коррелированны друг с другом.

Причина: При гетероскедастичности распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна.

Последствия нарушения условия гомоскедастичности случайных возмущений:

1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от Метода Наименьших Квадратов и более эффективные оценки

2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки

7.Динамическая модель из одновременных линейных уравнений (привести пример)

Экономические модели, значения переменных которых привязаны к моменту времени, называются динамическими.

Примером системы одновременных уравнений может служить модель спроса и предложения, включающая три уравнения: И еще один пример рядом.