Вопрос №23

Угол между прямыми на плоскости. Условие параллельности и перпендикулярности прямых. Определение. Если заданы две прямые y = k₁x + b₁, y = k₂x + b₂, то острый угол между этими прямыми будет определяться как . Две прямые параллельны, если k₁ = k₂. Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА, В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Вопрос №24

Различные виды уравнений плоскости в пространстве.

У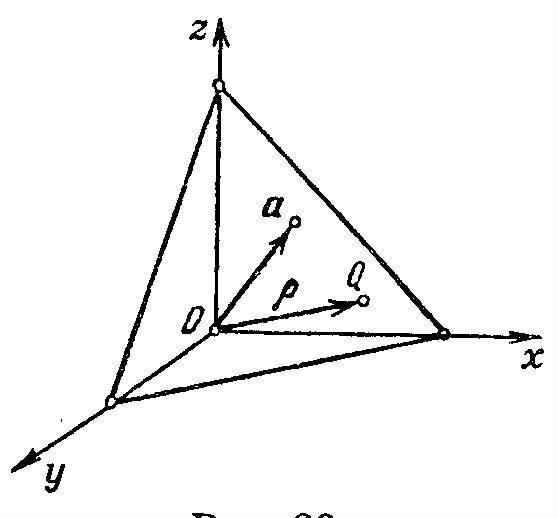равнение плоскости в нормальном виде. В пространстве R3, где введена прямоугольная система координат x, y, z, зададим вектор а, выпущенный из начала О. Через конец а проведем плоскость П перпендикулярно к а. Произвольную (текущую) точку плоскости П обозначим через Q = (x,y,z). Буква р обозначает радиус-вектор точки Q.

Пусть р = |a| - длина вектора а и V = (cos£, cosß, cosγ) – единичный вектор, направленный в ту же сторону что и а. Здесь £, ß, γ – углы, образуемые вектором V соответственно с положительными направлениями осей x,y,z. Проекция любой точки Q Є П на вектор V есть, очевидно, величина постоянная, равная p: (p,V) = p(p>=0) (1). Уравнение (1) имеет смысл и при р=0. В этом случае плоскость П проходит через начало координат О (а=0) и V – единичный вектор, выпущенный из О перпендикулярно к П, неважно в каком направлении, т.е. вектор V определяется с точностью до знака. Уравнение (1) есть уравнение плоскости П в векторной форме. В координатах оно записывается так: xcos£+ycosß+zcosγ=p (p>=0) (1’) и называется уравнением плоскости в нормальном виде.

Уравнение плоскости в общем виде. Если уравнение (1’) умножить на какое-либо не равное 0 число, то получим эквивалентное ему уравнение в виде: Ax+By+Cz+D=0 (2), определяющую ту же плоскость. Здесь числа А,В,С не равны нулю одновременно. Уравнение (2), где числа А,В,С не равны нулю, называется уравнение плоскости в общем виде.

Уравнение плоскости в отрезках. Если числа A,B,C,D не равны 0, то уравнение (2) можно записать так: x\a+y\b+z\c=1 где а=-D\A, b=-D\B, c=-D\c.

Уравнение плоскости, проходящее через точку. Если точка (x⁰, y⁰, z⁰) лежит на плоскости (2), то ее координаты удовлетворяют уравнению (2): Аx⁰+By⁰+Cz⁰+D=0 (3). Вычитая (3) из (2), получим: A(x-x⁰)+B(y-y⁰)+C(z-z⁰)=0.

Вопрос №25

Различные виды уравнений прямой в пространстве.

Общие уравнения прямой в пространстве. Линия в трехмерном пространстве определяется, вообще говоря, пересечением двух поверхностей, т.е. описывается системой двух уравнений.

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей и, следовательно, описывать системой двух линейных уравнений:

A₁x + B₁y + C₁z + D₁ = 0 A₂x + B₂y + C₂z + D₂ = 0

при условии, что эти плоскости непараллельные, т.е. их нормальные векторы неколлинеарны. Эта система уравнений называется общими уравнениями прямой в пространстве.

Каноническое. ((x-x₀)\a₁)=((y-y₀)\a₂)=((z-z₀)\a₃).

Параметрическое. Система: (x=x₀+a₁*t) (y=y₀+a₂*t) (z=z₀+a₃*t)