Вопрос №15

Полярные координаты на плоскости. О - полюс, Ox - полярная ось, - полярный радиус,- полярный угол. Главные значенияи:(иногда).

Выражение декартовых прямоугольных координат через полярные:

Выражение полярных координат через декартовы прямоугольные:

Сферические и цилиндрические координаты в пространстве.

Цилиндрические координаты. Главные значения ,,:

Связь между декартовыми прямоугольными и цилиндрическими координатами:

С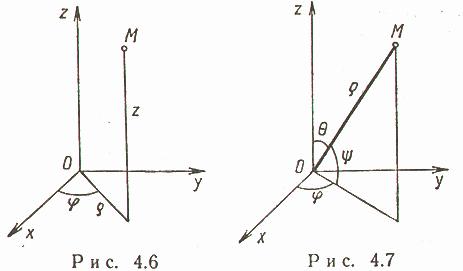ферические координаты. Главные значения ,,:

Иногда вместо рассматривают:

Вопрос №16

Проекции векторов. Обозначения: - проекции векторана ось l;- величина проекции векторана ось l. Свойства проекций:

Составляющие (компоненты) вектора:

Координаты вектора :(- углы, образуемые вектором с положительными направлениями осей координат Ox, Oy, Oz прямоугольной декартовой системы координат).

• , ,называются направляющими косинусами векторагдеЕсли- единичный вектор в направлении, то

Вопрос №17

Линейная зависимость векторов.

Векторы называютсялинейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно a_i, т.е. . Если же только при a_i = 0 выполняется , то векторы называются линейно независимыми.

Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

Свойство 6. Любые 4 вектора линейно зависимы.

Условия коллинеарности, ортогональности и компланарности векторов.

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы называются ортогональными, если их скалярное произведение равно нулю.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Вопрос №18

Преобразование декартовой прямоугольной системы координат на плоскости.

Параллельный сдвиг координатных осей.

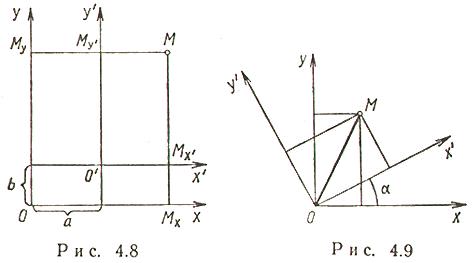
Поворот координатных осей.

Параллельный сдвиг и поворот координат осей.

Вопрос №19

Скалярное произведение и его свойства.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е. Из определения следуетгде φ - угол между векторами. Скалярная величинаназываетсяпроекцией вектора на вектор .

В зависимости от значения угла между векторами, проекция может принимать отрицательные, положительные или нулевое значения.

Теперь можно написать . Из определения скалярного произведения следует, что если векторы ортогональны, то(условие ортогональности ненулевых векторов).

Свойства скалярного произведения.