ТПУ Линейная алгебра 1курс ИДЗ №1

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Национальный исследовательский Томский политехнический Университет»

Институт

дистанционного образования

линейная алгебра

Индивидуальное домашнее задание № 1

_{вариант №1}

по дисциплине:

Линейная алгебра и аналитическая геометрия

Исполнитель:
студент группы					18.11.2013
Руководитель:
преподаватель			.

Томск  2013

Вариант № 1

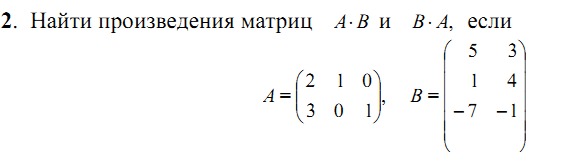
Решение:

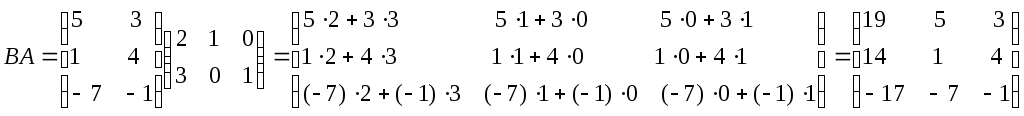
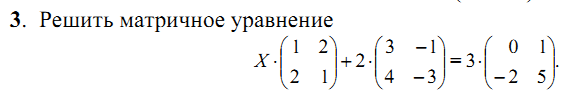
Решение:

Выполним вначале умножение матриц на число и упростим уравнение:

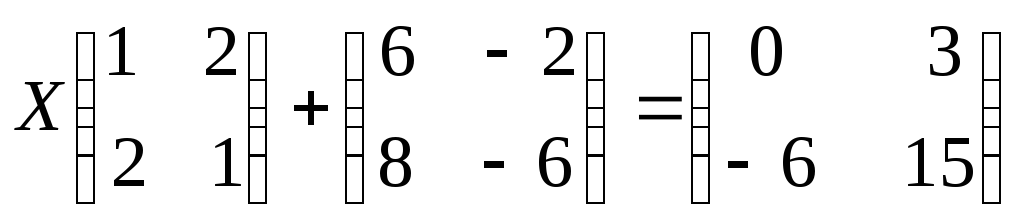
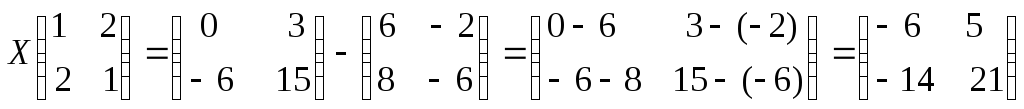
Обозначим ,

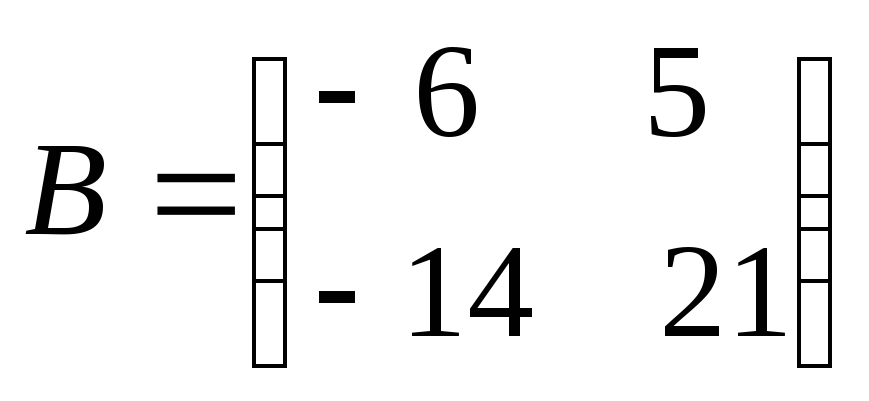
Тогда получим матричное уравнение вида , решение которого , где А^-1 - это матрица, обратная матрице А.

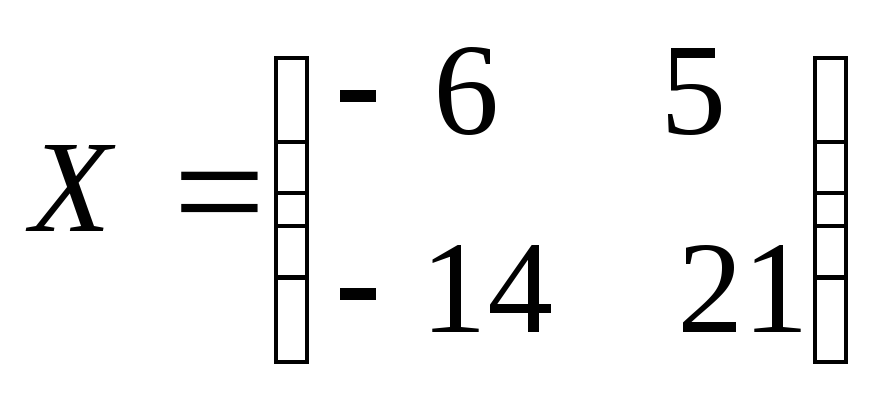
Найдем А^-1 по известной схеме:

1)

2)

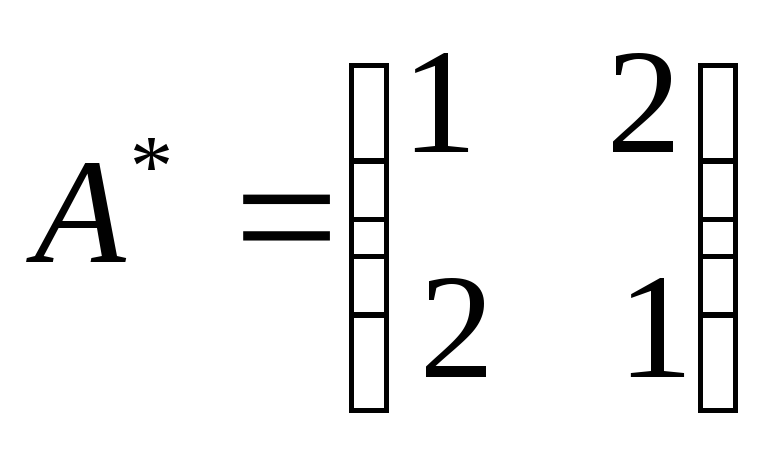
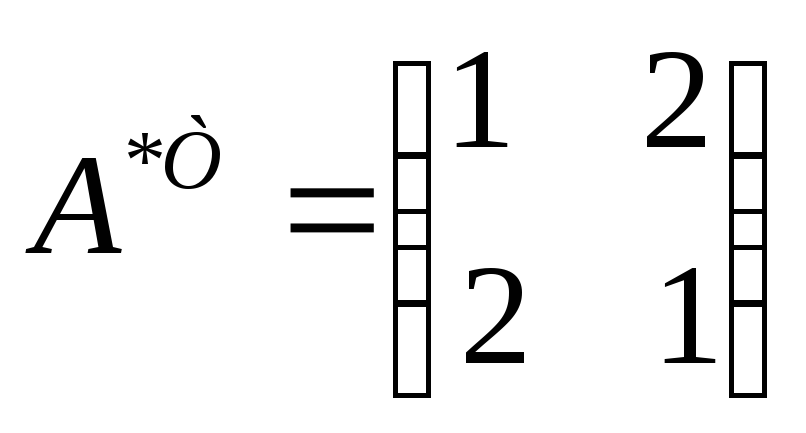
4)

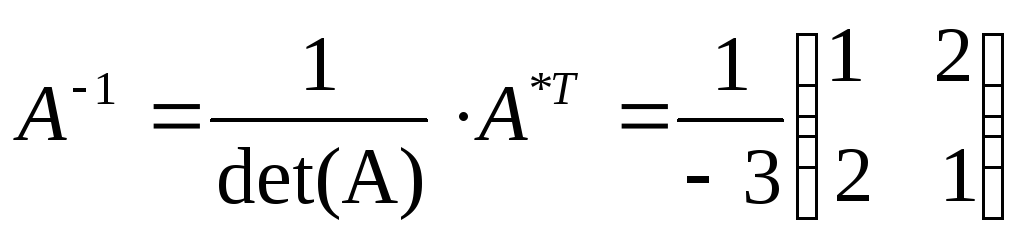
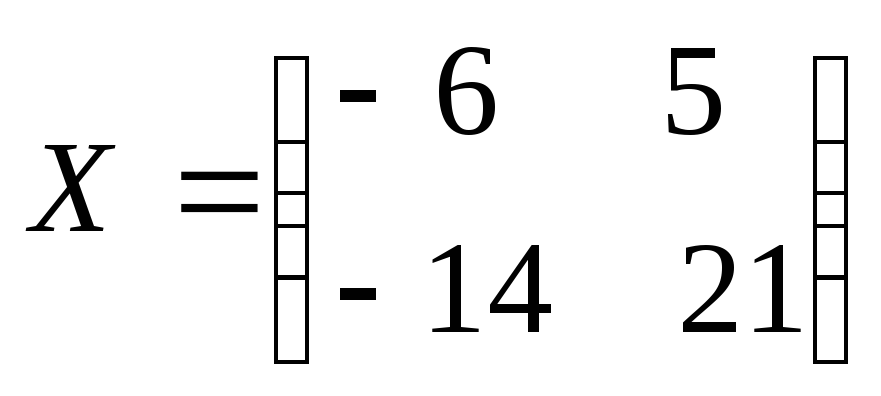
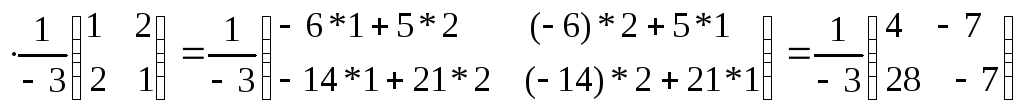
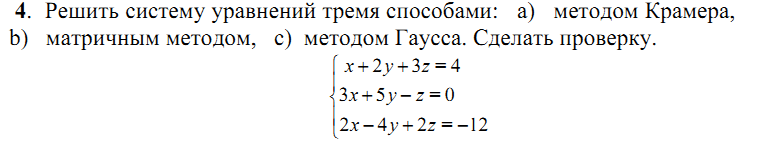
1. Метод Крамера

1)Вычислим главный определитель системы, который составляется из коэффициентов при неизвестных.

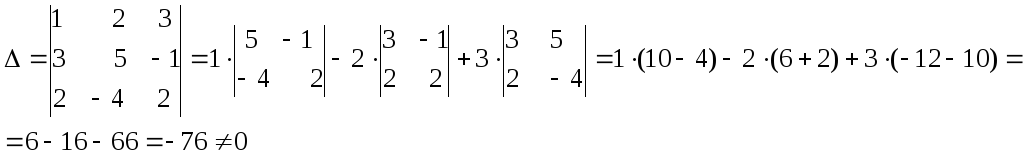
2)Вычислим побочные определители системы

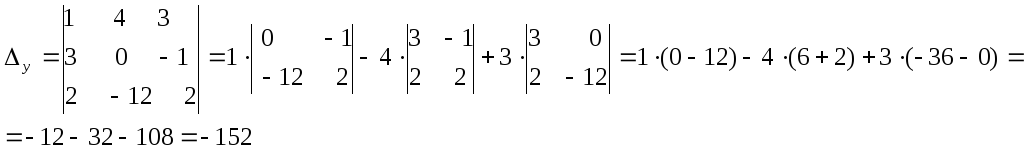
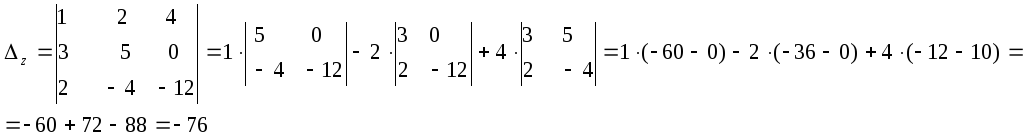
Решение системы находим по формулам Крамера

2. Матричный метод

1) обозначим матрицы

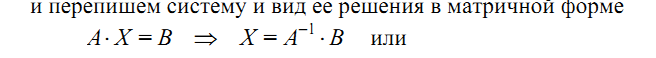
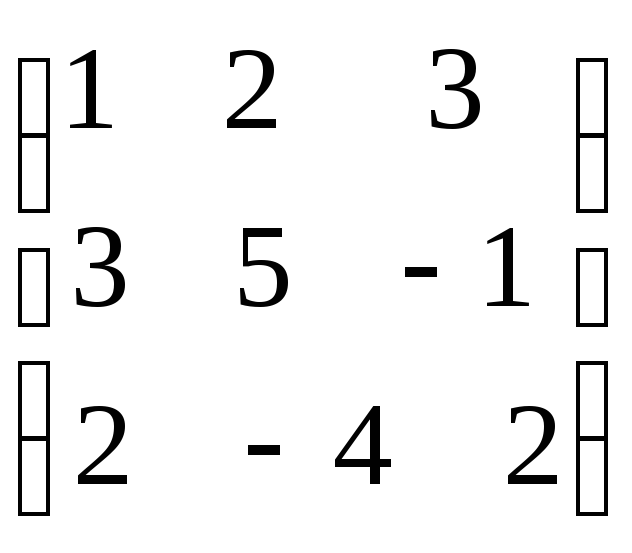
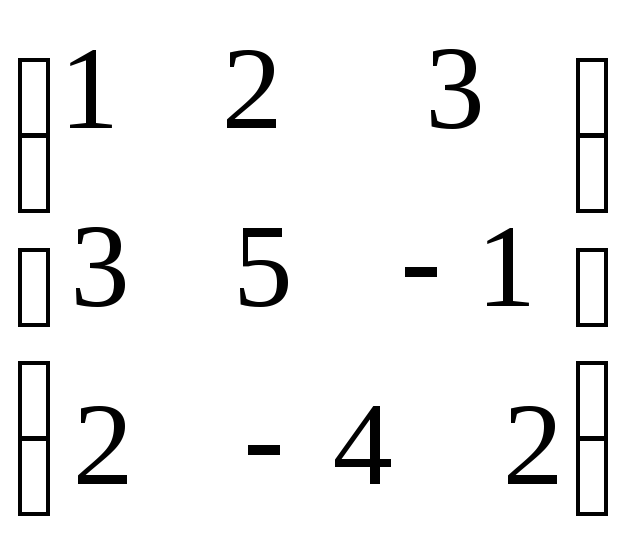
_{2) Находим обратную матрицу А}^-1 _{согласно схеме}

_{Находим определитель данной матрицы}

Находим алгебраические дополнения для каждого элемента матрицы А:

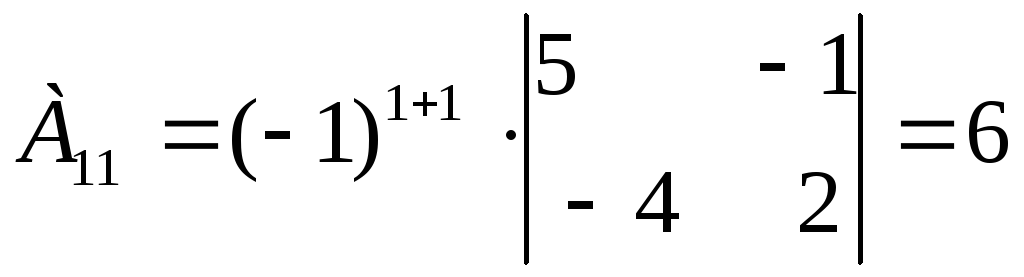
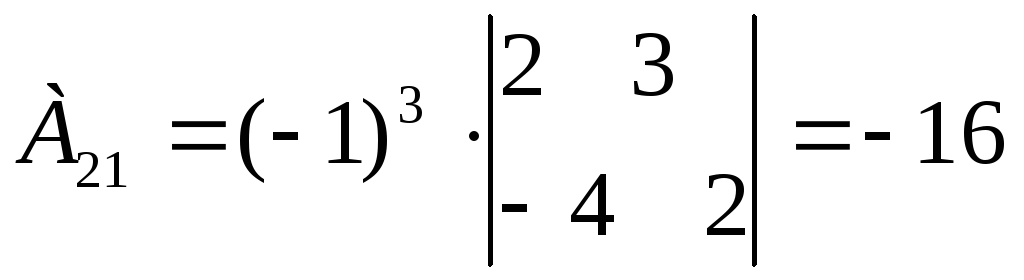
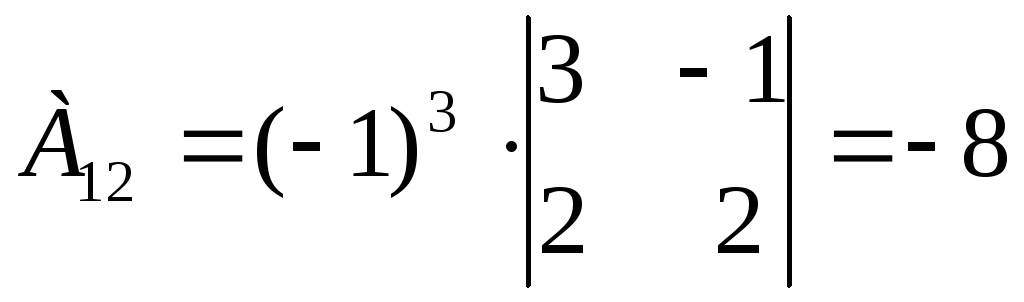
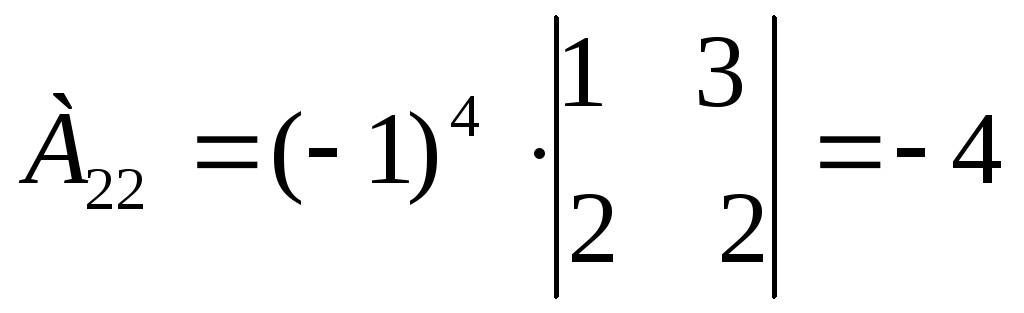
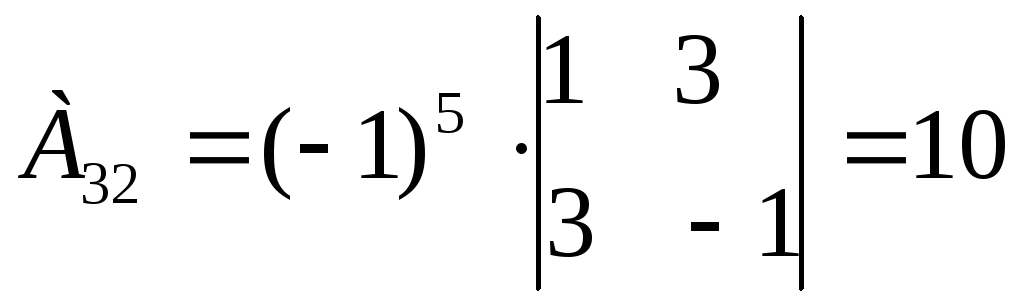
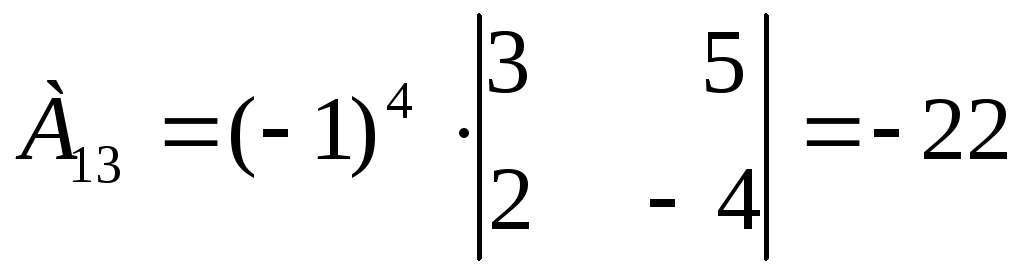
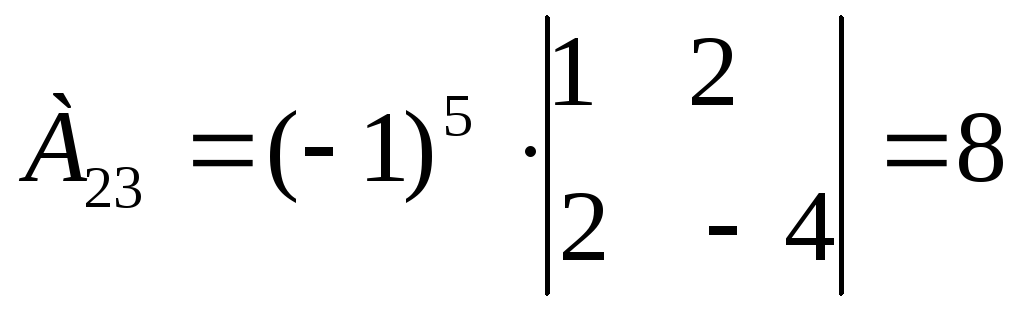
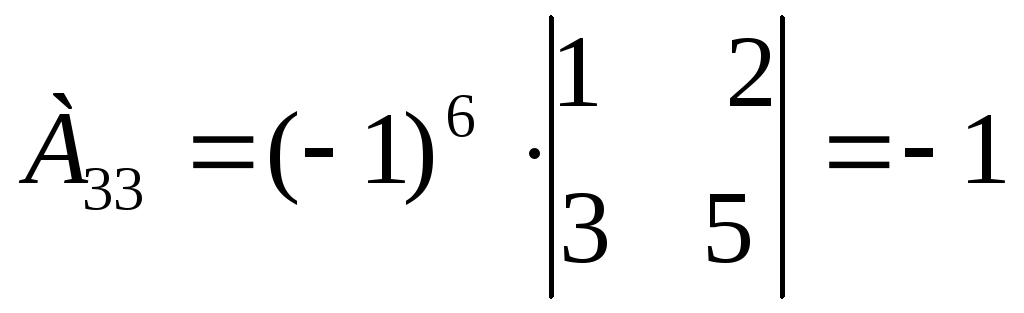
Вычисляем обратную матрицу А^-1:

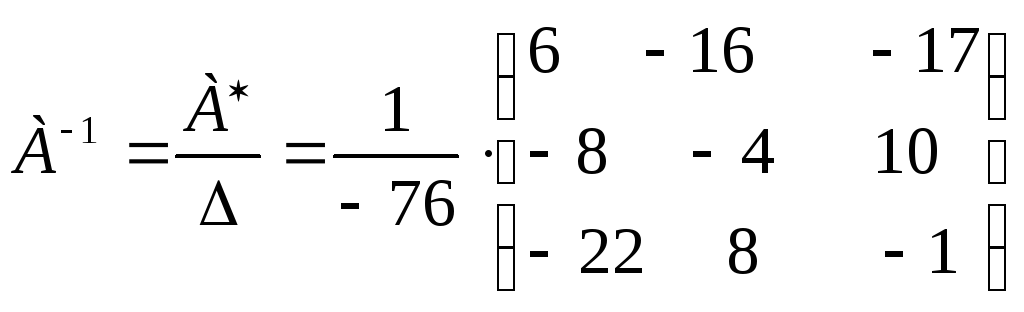
Решение системы уравнений Х=А^-1В

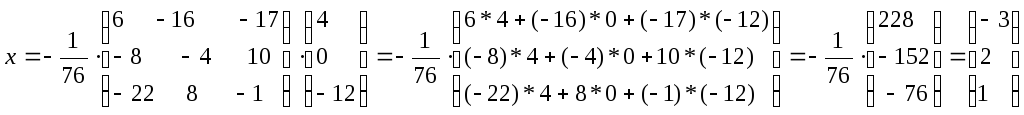
3. Метод Гаусса

1) Выпишем расширеную матрицу системы и преобразуем её

Умножаем строки 1 на (-3) и прибавляем строку 2, затем умножаем строку 1 на (-2) и прибавляем строку 3. получим.

умножаем строку 2 на (-8) и прибавляем строку 3. получим.

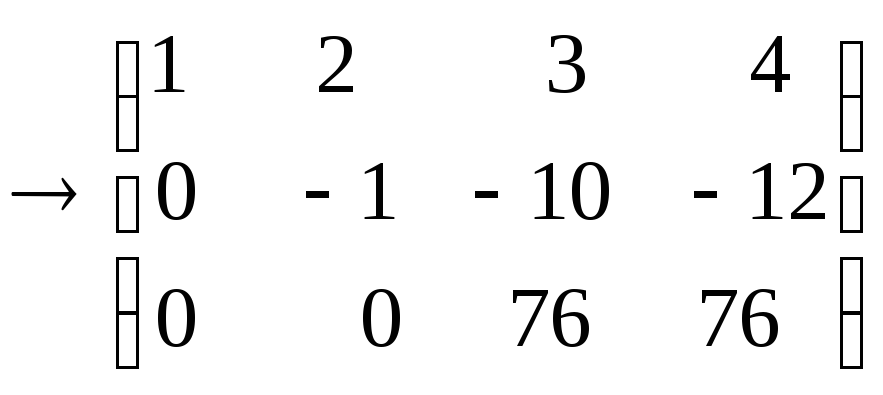
_{2) Выписываем эквивалентную систему и её решение}

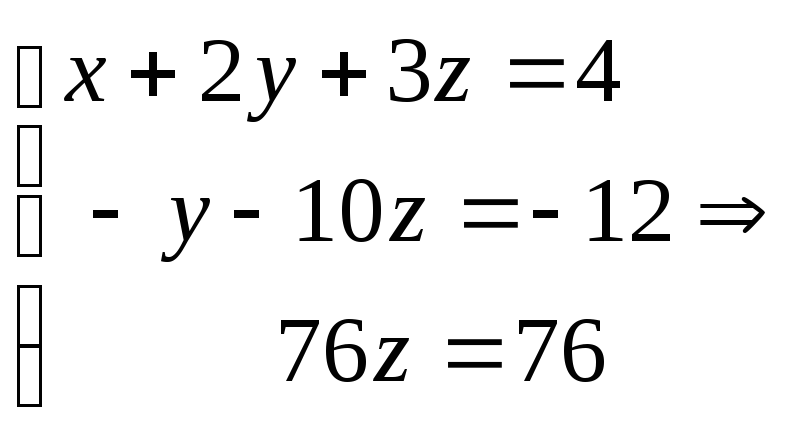
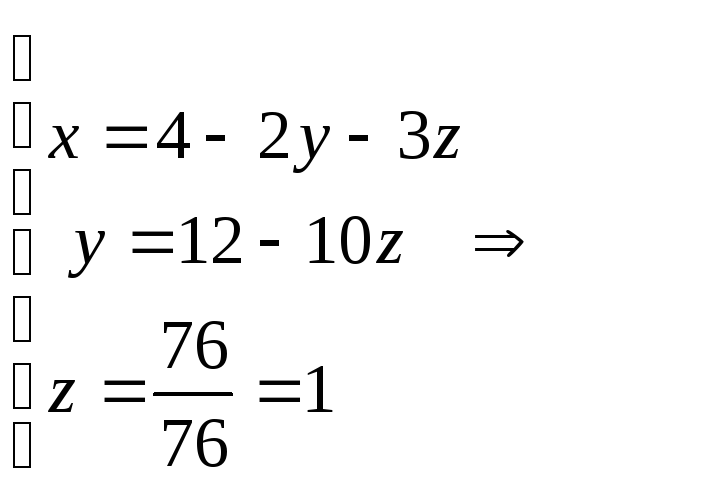
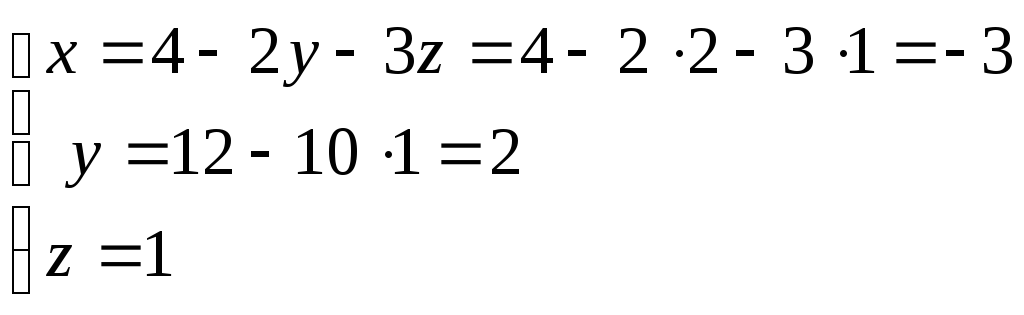
Ответ: х=-3, y=2, z=1

Список литературы по дисциплине «Линейная алгебра и аналитическая

геометрия»

1. Бугров Я.С., Никольский С.Н. Элементы линейной алгебры и аналитической геометрии.

М.: Наука, 2003г.

2. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры.- М.: Наука, 2002г.

3. Данко П.Е., Попов А.Г.Кожевникова Т.Я.Высшая математика в упражнениях и задачах.-

М.: Высшая школа, 2005г., ч.1

4. Письменный Д.Т.Конспект лекций по высшей математике: Полный курс.- М.:Айрис-

пресс,2004г.

5. Проскуряков И. В. Сборник задач по линейной алгебре.- М.: Наука, 2001.

6. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, 2005г.

7. Шнейдер В.Е. Краткий курс высшей математики. - М.: Высшая школа, 1999г. Т.1,2

8. Смирнов В.И. Курс высшей математики. – М.: Наука. 2001г.

9. Воеводин В.В. Линейная алгебра.- М.: Наука, 1980г.

10. Проскуряков И. В. Сборник задач по линейной алгебре.- М.: Наука, 1970г.

19