Ділення відрізка у даному відношенні.

Задані точки і . Знайти координати точки , що лежить на прямій АВ і ділить відрізок АВ у відношенні

:  

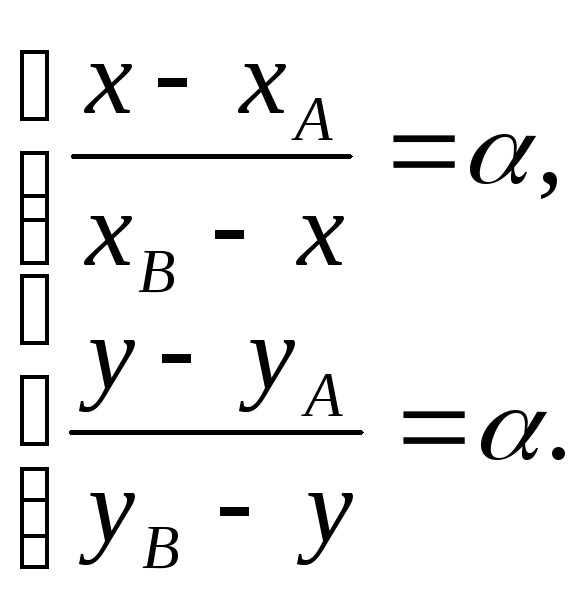
З першої рівності системи маємо:

Аналогічно з другого рівняння системи знаходимо:

Отже

Якщо , то ,

Контрольні запитання.

1. Що називається вектором?

2. Які вектори називаються колінеарними?

3. Які дії виконуються над векторами в геометричній формі? Пояснити на прикладах.

4. Які дії виконуються над векторами в координатній формі? Пояснити на прикладах.

5. Що називається скалярним добутком векторів?

6. Сформулювати властивості скалярного добутку векторів.

7. Що називається векторним добутком векторів?

8. Сформулювати властивості векторного добутку векторів.

9. Що називається мішаним добутком векторів?

10. Що називається базисом?

11. Які вектори називаються компланарними?

12. Як обчислити координати точки, яка ділить даний відрізок у даному відношенні?

Література.

А.П.Рябушко, В.В. Бархатов, В.В.Державець, І.Є. Юруть. Збірник індивідуальних завдань з вищої математики. Розділ 2.

Аналітична геометрія.

План.

1. Пряма на площині. Відповідні рівняння.

2. Взаємне розміщення прямих на площині.

3. Нормальне рівняння прямої.

4. Рівняння площини.

5. Рівняння площини у відрізках на осях.

6. Взаємне розміщення двох площин.

7. Рівняння площини, що проходить через три точки.

8. Кут між двома площинами.

9. Рівняння прямої у просторі.

10. Кут між прямою і площиною.

11. Рівняння площини, яка проходить через задану пряму, перпендикулярно до заданої площини.

12. Рівняння площини, яка проходить через дві паралельні прямі.

13. Рівняння площини, яка проходить через дві прямі, що перетинаються.

14. Рівняння площини, яка проходить через задану пряму і задану точку.

Пряма на площині. Відповідні рівняння.

Поняття лінії є одним з найскладніших понять математики.

Рівнянням лінії в декартових координатах на площині називається рівняння виду , яке задовольняють координати будь – якої точки цієї лінії і не задовольняють координати будь – якої точки, що не належить цій лінії.

1. Загальне рівняння прямої на площині:

Якщо А=0,

- рівняння прямої, паралельної осі Ох.

- рівняння осі абсцис (Ох)

Якщо В=0, то

- - рівняння прямої, паралельної осі Оу

- рівняння осі ординат (Оу)

2. Рівняння прямої у відрізках на осях.

Позначимо: , тоді

3. Рівняння прямої з кутовим коефіцієнтом.

Позначимо

ОВ=в – початкова координата, - кутовий коефіцієнт прямої.

Якщо пряма проходить через початок координат, то

4. Рівняння прямої, що проходить через дві точки.

Зафіксуємо на прямій дві точки і (координати відомі).

АВС:

Отже (1) - кутовий коефіцієнт прямої.

Зафіксуємо тепер точку , а точка має поточні координати.

АВС:

Отже  (2) - рівняння прямої, яка проходить через задану точку і має заданий кутовий коефіцієнт.

В рівняння (2) підставимо значення к з рівності (1)

- рівняння прямої, що проходить через дві точки.