Властивості визначеного інтеграла.

1). Якщо , то

2). Сталий множник можна виносити з-під знака визначеного інтеграла, тобто

3). Якщо та інтегровні на [a; b], то

4). Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл змінить лише свій знак на протилежний, тобто

5). Визначений інтеграл з однаковими межами інтегрування дорівнює нулю

Для обчислення визначеного інтеграла застосовують формулу, яка зв’язує визначений інтеграл та первісну функцію. Ця формула має вигляд

,

де – первісна функція, а та – межі (границі) інтегрування і її називають формулою Ньютона-Лейбніца.

Застосування визначених інтегралів для розв’язку геометричних задач.

Площу криволінійної трапеції для неперервної на відрізку функції , згідно геометричного змісту інтеграла, обчислюють за формулою

.

Об’єм тіла обертання криволінійної трапеції з основою навколо осі , яка обмежена неперервною функцією , обчислюється за формулою

.

Якщо криволінійна трапеція з основою обертається навколо осі , то об’єм тіла обертання обчислюють за формулою

,

де неперервна для всіх .

Приклад. Обчислити площу фігури, яка обмежена лініями та .

Побудуємо фігуру, як показано на малюнку. Для чого знайдемо точки перетину ліній. Для цього розв’яжемо систему:

.

Площа фігури дорівнює різниці площ двох криволінійних трапецій, площі яких можна обчислити . Одержимо:

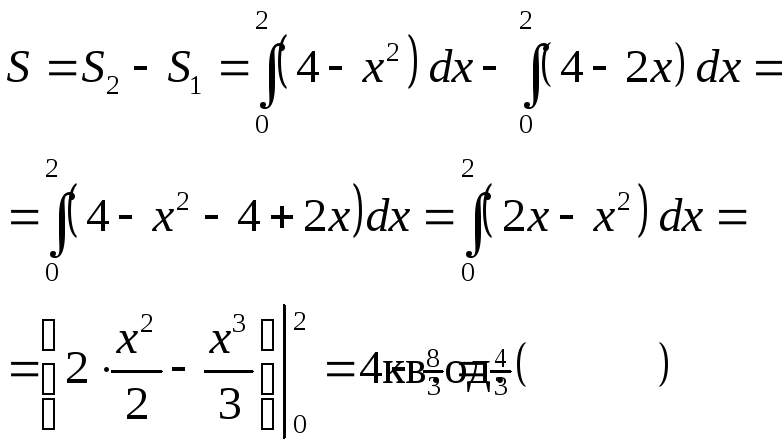
П

Рис. 11

риклад. Обчислити об’єми тіл обертання навколо осей та фігури, яка обмежена лініями та .

Обчислимо об’єми тіл, які утворюються при обертанні фігури навколо осей. Знайдемо точки перетину ліній:

Одержали дві точки з координатами та . Зобразимо ці тіла схематично як показано на малюнках:

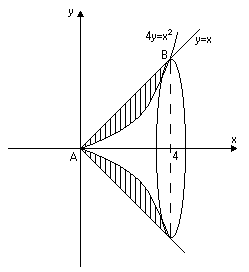
1

Рис. 12

) Об’єм тіла обертання навколо осі дорівнює різниці двох об’ємів тіл:

2) Аналогічно обчислюємо об’єм тіла обертання навколо осі :

Контрольні запитання.

9. Що називається первісною та невизначеним інтегралом?

10. Які властивості невизначеного інтегралу відомі ?

11. Запишіть первісні основних елементарних функцій.

12. Які методи знаходження невизначених інтегралів існують? Поясніть їх застосування на прикладах.

13. Які властивості визначеного інтегралу відомі ?

14. Запишіть формулу Ньютона-Лейбниця, поясніть її складові.

15. Для чого застосовується визначений інтеграл? Наведіть приклади.

Завдання для самостійного виконання.

Задача 1. Розв’язати систему за правилом Крамера, методом Гаусса та матричним способом.

Варіант	Система		Варіант	Система
1		-1	2		1
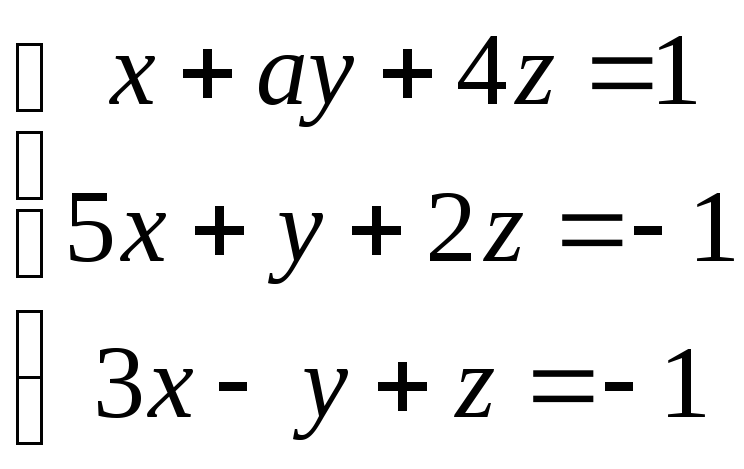
3		1	4		2
5		-1	6		1
7		0	8		4
9		-1	10		1
11		3	12		1
13		3	14		5
15		-2	16		1
17		1	18		-1
Варіант	Система		Варіант	Система
19		1	20		0
21		4	22		2
23		0	24		-2
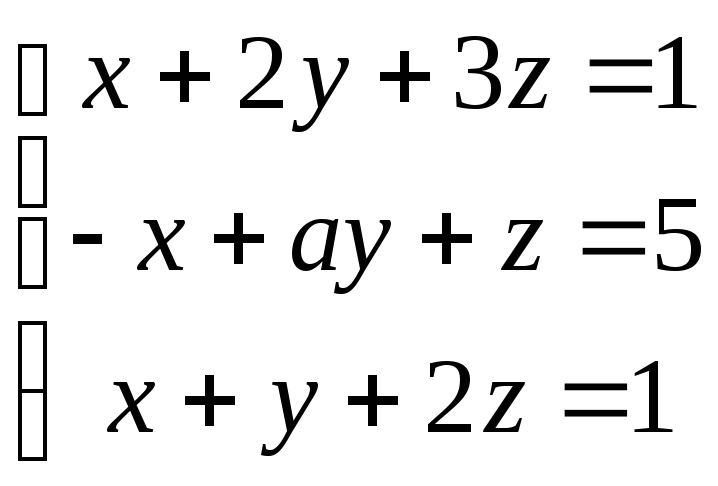
25		-1	26		1
27		0	28		1
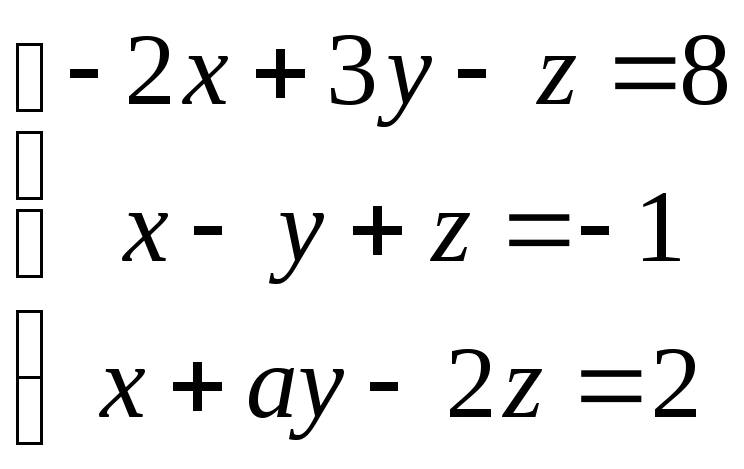
29		5	30		3
31		0	32		2
33		2	34		-1
35		5	36		-16
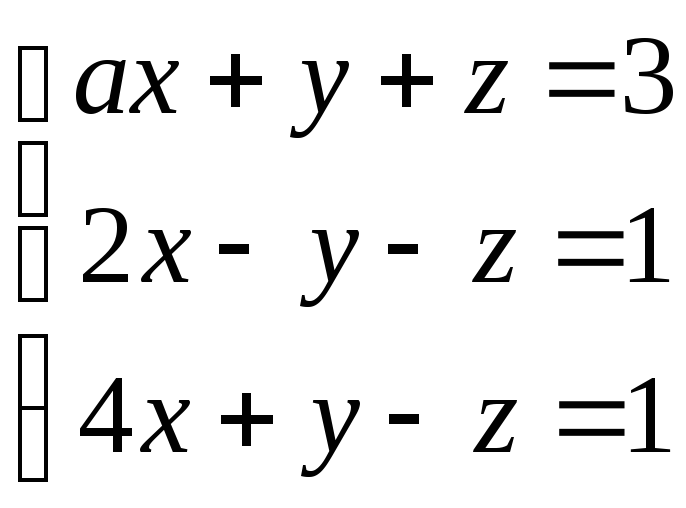
37		-1	38		0
Варіант	Система		Варіант	Система
39		-2	40		-3

Задача 2. Написати розкладання вектора за векторами , , .

Варіант
1	(5;-9;13)	(3;0;-1)	(7;0;1)	(4;2;-2)
2	(8;9;4)	(1;-2;2)	(1;1;1)	(2;3;1)
3	(15;-5;-6)	(3;7;0)	(2;3;-1)	(-1;6;1)
4	(8;-4;-5)	(3;0;0)	(-2;1;5)	(-1;3;5)
5	(5;3;2)	(2;1;0)	(1;0;1)	(3;2;0)
6	(8;-3;4)	(4;2;1)	(2;3;1)	(0;0;3)
7	(0;6;2)	(1;2;3)	(3;-2;2)	(2;-1;0)
8	(-10;8;15)	(-2;1;6)	(-2;2;1)	(0;1;5)
9	(4;-8;10)	(3;-1;0)	(7;1;0)	(4;-2;2)
10	(1;7;4)	(2;-2;1)	(1;1;1)	(1;3;2)
11	(7;-7;-12)	(3;0;7)	(2;-1;3)	(-1;1;6)
Варіант
13	(-7;9;11)	(0;3;-1)	(0;7;1)	(2;4;-2)
14	(7;9;6)	(-2;1;2)	(1;1;1)	(3;2;1)
15	(1;14;-5)	(7;3;0)	(3;2;-1)	(6;-1;1)
16	(7;-1;0)	(0;3;0)	(1;-2;5)	(3;-1;5)
17	(8;3;4)	(2;0;1)	(1;1;0)	(3;0;2)
18	(10;0;5)	(2;3;1)	(0;0;3)	(4;1;2)
19	(8;5;1)	(2;3;1)	(-2;2;3)	(-1;0;2)
20	(7;9;-8)	(1;6;-2)	(2;1;-2)	(1;5;0)
21	(-7;10;1)	(-1;0;3)	(1;0;7)	(-2;2;4)
22	(7;5;2)	(0;1;1)	(-2;1;0)	(3;0;1)
23	(-6;6;-6)	(0;3;7)	(-1;2;3)	(1;-1;6)
24	(15;9;0)	(0;1;2)	(0;-1;1)	(5;2;-3)
25	(2;8;8)	(3;7;4)	(0;0;2)	(-1;1;-2)
26	(-3;5;12)	(1;1;2)	(-2;1;3)	(2;1;1)
Варіант
27	(3;18;19)	(3;-2;-1)	(0;1;3)	(0;5;5)
28	(7;4;13)	(2;1;3)	(1;0;2)	(0;1;0)
29	(15;20;9)	(4;2;0)	(1;3;0)	(2;1;3)
30	(2;-1;1)	(3;0;1)	(-1;2;2)	(0;1;1)
31	(1;-10;2)	(2;-1;0)	(-1;1;3)	(2;0;-2)
32	(2;2;8)	(3;1;0)	(2;0;2)	(1;1;-1)
33	(7;4;5)	(-1;1;0)	(1;2;-1)	(3;0;3)
34	(0;10;5)	(1;1;-1)	(0;4;1)	(2;1;-1)
35	(3;-1;9)	(2;0;0)	(-3;1;1)	(0;-1;1)
36	(1;18;16))	(0;1;1)	(2;0;4)	(-2;1;-1)
37	(-1;5;4)	(1;0;1)	(-3;1;0)	(2;2;1)
38	(4;8;8)	(2;1;0)	(-1;1;0)	(4;1;1)
39	(5;-5;5)	(2;2;1)	(0;-1;1)	(0;1;2)
40	(0;7;3)	(1;1;1)	(0;-1;2)	(3;1;1)

Задача 3. Дано координати векторів і . Обчислити координати векторів і . Перевірити колінеарність та ортогональність векторів і .

Варіант
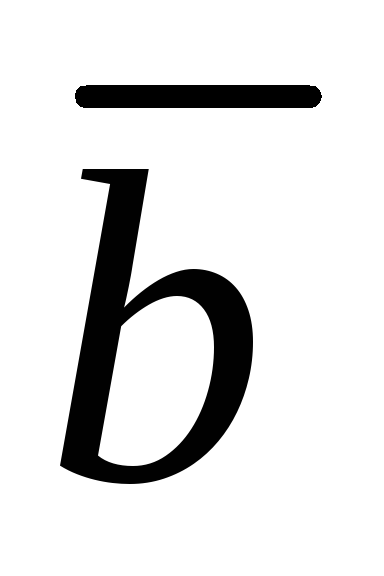
1	(8;1;9)	(6;5;1)	6	-3	-2	1
2	(1;-2;2)	(6;3;2)	7	3	7	-3
3	(1;-1;-1)	(4;2;2)	12	1	2	-3
4	(11;-1;5)	(1;1;9)	3	-2	-6	4
5	(-2;2;1)	(-1;1;-4)	5	-1	2	5
6	(3;-6;2)	(-2;-1;2)	3	-7	3	7
7	(4;1;12)	(4;3;6)	-3	4	4	-3
8	(2;1;15)	(8;-1;1)	3	-4	-9	12
9	(1;2;4)	(3;-4;-4)	6	-2	-3	1
10	(4;2;-4)	(2;6;3)	7	5	-7	6
11	(9;2;-10)	(1;-2;4)	1	-3	-2	6
12	(2;9;7)	(4;5;-9)	4	-3	-12	9
13	(5;3;0)	(1;5;-2)	6	-3	-2	1
Варіант
14	(2;2;8)	(4;-6;4)	2	-1	-6	3
15	(-1;-3;3)	(3;3;7)	3	9	-1	-3
16	(6;1;1)	(2;2;4)	2	1	6	3
17	(1;1;-1)	(2;-1;1)	5	-3	6	5
18	(4;4;4)	(1;5;-2)	4	-2	-2	1
19	(-1;-2;3)	(1;-2;-1)	3	-1	1	7
20	(1;-5;0)	(3;-9;2)	6	-2	-3	1
21	(3;4;5)	(3;4;-5)	4	-1	1	4
22	(6;2;1)	(4;2;-4)	2	-1	-4	2
23	(11;4;1)	(1;4;5)	5	-3	-10	6
24	(4;-3;8)	(1;4;2)	4	-2	-2	1
25	(5;-4;3)	(5;4;-3)	2	-3	3	2
26	(5;-8;-2)	(1;-6;10)	2	-3	3	-2
27	(3;0;-1)	(2;0;6)	4	1	2	-2
Варіант
28	(3;-6;6)	(6;3;-2)	7	-9	7	9
29	(-2;6;1)	(7;1;-2)	2	-1	3	5
30	(2;0;-1)	(5;-4;2)	3	-1	3	1
31	(7;5;-2)	(4;2;4)	2	-4	-1	2
32	(5;-3;1)	(3;3;0)	-1	2	2	-4
33	(11;1;4)	(1;4;-5)	2	-3	-2	5
34	(9;1;1)	(-1;4;4)	1	2	-1	-2
35	(3;7;7)	(-4;2;2)	1	-2	4	3
36	(4;-2;-2)	(1;3;5)	-2	-4	-3	2
37	(9;-3;1)	(1;8;4)	-1	3	-3	1
38	(7;0;3)	(2;-4;1)	-1	2	-2	3
39	(-1;-1;1)	(2;3;0)	5	-2	3	1
40	(-2;-2;1)	(-3;71)	4	-3	1	2

Задача 4. Дано прямокутні декартові координати точок A, B, C, D . Обчислити:

1) кут між векторами і ;

2) проекцію вектора на напрям вектора ;

3) площу ;

4) об’єм тетраедра з вершинами в точках A, B, C, D та його висоту, опущену з вершини D на грань ABC.

Варіант	А	В	С	D
1	(3;0;-1)	(2;3;2)	(6;1;-5)	(-9;10;-6)
2	(0;2;-2)	(1;9;3)	(6;-6;-2)	(3;-2;8)
3	(12;2;3)	(-7;-5;0)	(-4;-8;-5)	(-4;0;-3)
4	(2;3;0)	(4;1;-3)	(6;3;6)	(9;5;-9)
5	(3;0;3)	(2;3;0)	(4;3;2)	(-3;3;6)
6	(2;2;3)	(0;2;4)	(3;-1;5)	(0;1;-1)
7	(1;2;0)	(3;0;-3)	(5;2;6)	(6;4;-4)
8	(2;2;0)	(3;4;2)	(4;3;2)	(6;10;-7)
9	(1;5;-5)	(-3;6;5)	(-2;7;5)	(-4;8;10)
10	(0;4;-7)	(4;5;-4)	(-2;-2;0)	(5;5;4)
11	(-1;4;-3)	(4;1;0)	(2;3;-2)	(3;6;5)
12	(5;0;3)	(-1;2;0)	(1;-4;1)	(4;3;-6)
Варіант	А	В	С	D
13	(2;0;2)	(-1;1;4)	(3;2;0)	(3;-1;-3)
14	(2;3;1)	(2;0;3)	(1;2;0)	(-2;1;2)
15	(2;1;3)	(2;3;0)	(3;-1;2)	(3;2;1)
16	(2;3;-2)	(2;1;2)	(-1;0;7)	(1;-4;-3)
17	(4;11;0)	(-1;4;-4)	(-5;1;-2)	(2;0;3)
18	(0;3;5)	(0;-1;-3)	(4;1;0)	(8;-2;2)
19	(1;-2;2)	(-3;2;3)	(3;0;6)	(4;2;-3)
20	(2;4;1)	(5;0;3)	(4;1;2)	(-3;4;6)
21	(-1;0;0)	(1;4;3)	(4;2;-3)	(-3;8;4)
22	(-2;-4;7)	(3;2;-3)	(1;-2;0)	(-4;3;-7)
23	(3;-3;-2)	(6;-5;1)	(0;4;-2)	(-9;-7;8)
24	(2;0;3)	(3;2;3)	(2;2;5)	(7;-2;9)
25	(7;1;1)	(-2;-1;1)	(1;-3;-5)	(-6;5;-6)
26	(1;2;-1)	(2;5;0)	(6;-1;2)	(6;1;0)
Варіант	А	В	С	D
28	(2;2;1)	(2;1;0)	(4;1;5)	(4;3;-5)
29	(2;1;1)	(2;1;-1)	(4;4;5)	(1;6;-7)
30	(2;2;1)	(1;3;3)	(3;1;3)	(3;5;-4)
31	(0;2;2)	(4;-1;3)	(7;5;0)	(-2;-2;1)
32	(3;3;0)	(-1;4;2)	(5;-7;1)	(0;1;-8)
33	(2;1;2)	(3;0;4)	(-1;6;3)	(4;-3;0)
34	(3;3;2)	(0;1;4)	(2;1;1)	(6;1;7)
35	(-1;4;4)	(0;-3;6)	(2;-1;2)	(3;3;0)
36	(8;1;-2)	(1;3;0)	(-5;2;7)	(4;-1;-1)
37	(5;-3;-2)	(4;1;1)	(6;6;0)	(2;0;1)
38	(-1;3;2)	(4;-2;6)	(0;1;4)	(2;0;1)
39	(2;1;-1)	(0;-7;3)	(1;0;-2)	(4;1;1)
40	(0;7;-1)	(2;2;1)	(-3;4;3)	(6;0;-2)

Задача 5 Обчислити границі:

Варіант1 Варіант2

а) а)

б) б)

в) в)

Варіант3 Варіант4

а) а)

б) б)

в) в)

Варіант5 Варіант6

а) а)

б) б)

в) в)

Варіант7 Варіант8

а) а)

б) б)

в) в)

Варіант9 Варіант10

а) а)

б) б)

в) в)

5

Варіант11 Варіант12

а) а)

б) б)

в) в)

Варіант13 Варіант14

а) а)

б) б)

в) в)

Варіант15 Варіант16

а) а)

б) б)

в) в)

Варіант17 Варіант18

а) а)

б) б)

в) в)

Варіант19 Варіант20

а) а)

б) б)

в) в)

Варіант21 Варіант22

а) а)

б) б)

в) в)

Варіант23 Варіант24

а) а)

б) б)

в) в)

Варіант25 Варіант26

а) а)

б) б)

в) в)

Варіант27 Варіант28

а) а)

б) б)

в) в)

Варіант29 Варіант30

а) а)

б) б)

в) в)

Задача 6. Знайти точки розриву функцій та вказати їх тип. Зробити креслення.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

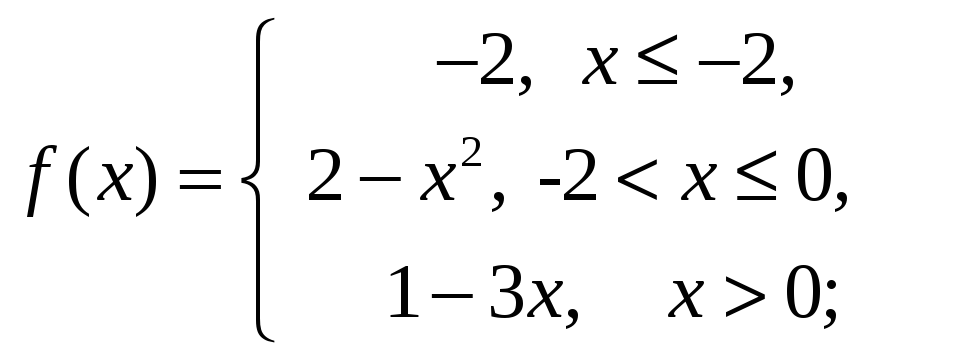
15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

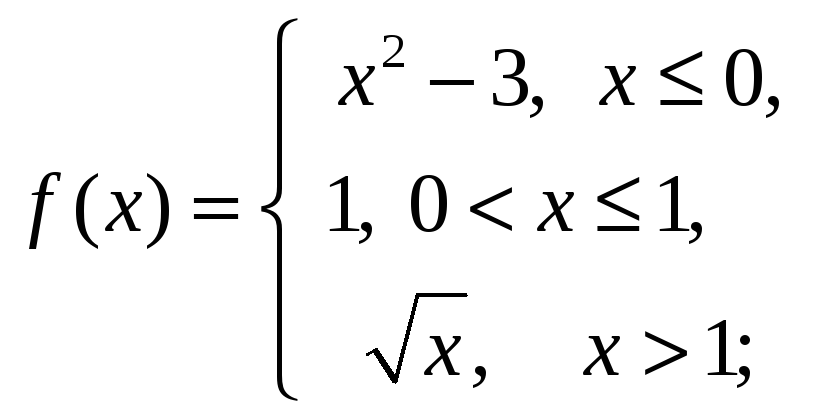
30.

Задача 7. Знайти похідні:

1. а) ; б) ; в)

2. а) ; б) ; в)

3. а) б) ; в)

4. а) ; б) ; в)

5. а) б) ; в)

6. а) ; б) ; в)

7. а) б) ; в)

8. а) ; б) ; в)

9. а) ; б) ; в)

10. а) б) ; в)

11. а) ; б) ; в)

12. а) б) ; в)

13. а) ; б) ; в)

14. а) б) ; в)

15. а) б) ; в)

16. а) ; б) ; в)

17. а) б) ; в)

18. а) ; б) ; в)

19. а) б) ; в)

20. а) ; б) ; в)

21. а) ; б) ; в)

22. а) б) ; в)

23. а) ; б) ; в)

24. а) б) ; в)

25. а) ; б) ; в)

26. а) б) ; в)

27. а) ; б) ; в)

28. а) ; б) ; в)

29. а) б) ; в)

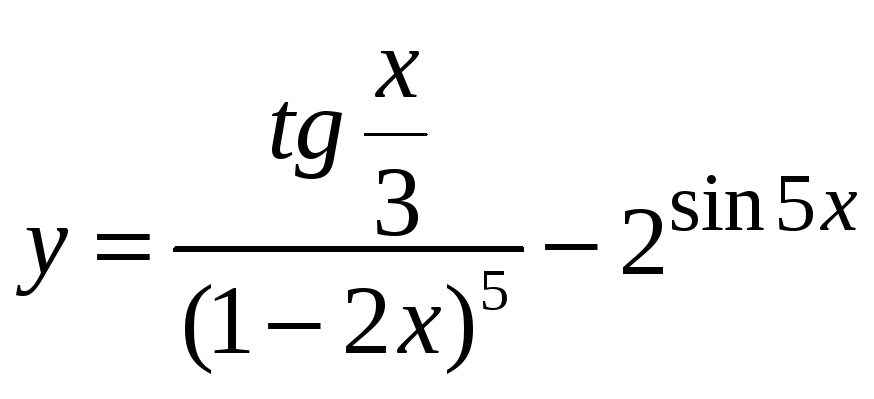30. а) ; б) ; в)

Задача 8. Скласти рівняння дотичної та нормалі до графіка функції в точці з абсцисою .

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

Задача 9. Знайти найбільше та найменше значення функції на відрізку.

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

29. 30.

Задача 10. Знайти невизначені інтеграли. В прикладах 1-2 отриманий результат перевірити диференціюванням.

- 1 -

1.1. 1.2.

1.3. 1.4.

1.5. 1.6.

1.7. 1.8.

1.9. 1.10

1.11. 1.12.

1.13. 1.14.

1.15. 1.16.

1.17. 1.18.

1.19. 1.20.

1.21. 1.22.

1.23. 1.24.

1.25. 1.26.

1.27. 1.28.

1.29. 1.30.

- 2 -

2.1. 2.2.

2.3. 2.4.

2.5. 2.6.

2.7. 2.8.

2.9. 2.10.

2.11. 2.12.

2.13. 2.14.

2.15. 2.16.

2.17. 2.18.

2.19. 2.20.

2.21. 2.22.

2.23. 2.24.

2.25. 2.26.

2.27. 2.28.

2.29. 2.30.

- 3 -

3.1. 3.2.

3.3. 3.4.

3.5. 3.6.

3.7. 3.8.

3.9. 3.10.

3.11. 3.12.

3.13. 3.14.

3.15. 3.16.

3.17. 3.18.

3.19. 3.20.

3.21. 3.22.

3.23. 3.24.

3.25. 3.26.

3.27. 3.28.

3.29. 3.30.

- 4 -

4.1. 4.2.

4.3. 4.4.

4.5. 4.6.

4.7. 4.8.

4.9. 4.10.

4.11. 4.12.

4.13. 4.14.

4.15. 4.16.

4.17. 4.18.

4.19. 4.20.

4.21. 4.22.

4.23. 4.24

4.25. 4.26.

4.27. 4.28.

4.29. 4.30.

- 5 -

6.1. 6.2.

6.3. 6.4.

6.5. 6.6.

6.7. 6.8.

6.9. 6.10.

6.11. 6.12.

6.13. 6.14.

6.15. 6.16.

6.17. 6.18.

6.19. 6.20.

6.21. 6.22

6.23. 6.24.

6.25. 6.26.

6.27. 6.28.

6.29. 6.30.

Задача 11. Обчислити площу фігури, обмеженої вказаними лініями:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. ;

19. ;

20. ;

21. ;

22. ;

23. ;

24. ;

25. ;

26. ;

27. ;

28. ;

29. ;

30. .

Міністерство освіти і науки України

Сумський державний університет

Машинобудівний коледж