Дії над векторами, заданими своїми координатами.

Якщо і , то

1. - множення вектора на число;

2. - додавання векторів;

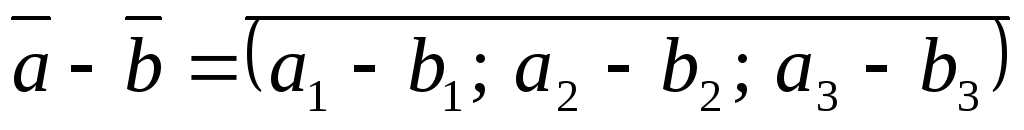3. - віднімання векторів.

Операції додавання, віднімання, множення вектора на число задовольняють слідуючим властивостям:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

Скалярний добуток векторів.

Скалярним добутком векторів і називається число, яке дорівнює сумі добутків відповідних координат: .

Скалярний добуток векторів дорівнює добутку модулів цих векторів на косинус кута між ними:

Кут між векторами знаходять за формулою:

Геометричні властивості скалярного добутку:

1. (умова перпендикулярності векторів);

2. 

3. 

4. 

Алгебраїчні властивості скалярного добутку:

1. 

2. 

3. 

4. 

Векторний добуток векторів.

Векторним добутком векторів і називається вектор (позначається ), який задовольняє слідуючи умови:

1. довжина вектора дорівнює площі паралелограма, побудованого на векторах і : , де ;

2. вектор перпендикулярний кожному з векторів і : ;

3. трійка векторів , і - права: напрям вектора такий, що при спостереженні з його кінця найменший кут від до здійснюється проти годинникової стрілки:

Властивості векторного добутку:

1.  (умова колінеарності векторів);

2. ;

3. ;

4. ;

Якщо вектори задано їхніми координатами і , то

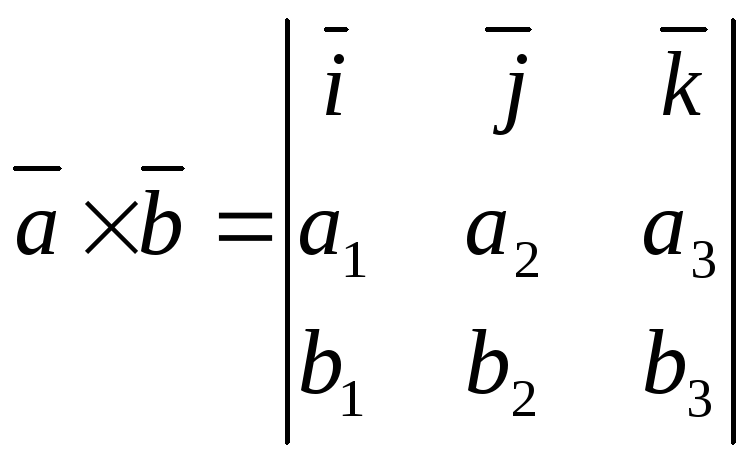
Мішаний добуток векторів.

Мішаним добутком векторів упорядкованої трійки векторів , і називається число, яке дорівнює векторному добутку , помноженому скалярно на вектор .

Якщо вектори , , задано своїми координатами , , , то їх мішаний добуток визначають за формулою

Геометричний зміст мішаного добутку векторів: модуль мішаного добутку векторів , і дорівнює об’єму паралелепіпеда, побудованого на цих векторах

а об’єм відповідної піраміди .

Необхідна і достатня умова компланарності або лінійної залежності векторів , і виражається рівністю .

Якщо , то упорядкована трійка векторів , і права (мал..1.), а якщо , то ліва (мал..2.).

мал. 1. мал..2.

Базис.

Лінійною комбінацією векторів з дійсними коефіцієнтами називається довільний вектор . Якщо вектор поданий у вигляді лінійної комбінації деяких векторів, то кажуть, що він розкладений за цими векторами.

Вектори називаються лінійно залежними, якщо існують такі числа , що і . Якщо рівність справджується лише при , то вектори називаються лінійно незалежними.

Два колінеарні вектори – лінійно залежні, а два не колінеарні вектори – лінійно незалежні.

Три компланарні вектори – лінійно залежні, а три не компланарні вектори - лінійно незалежні. Чотири вектори в тривимірному просторі завжди лінійно залежні.

Базисом векторів на площині називається упорядкована пара лінійно незалежних (неколінеарних) векторів і . Всякий вектор компланарний векторам і , які утворюють базис, можна подати у вигляді суми . Числа і називають координатами вектора у базисі і пишуть , сума - розклад вектора за цим базисом.

Базисом у просторі називається упорядкована трійка лінійно незалежних (некомпларних) векторів. Всякий вектор простору можна розкласти за базисом : , ,, називають координатами вектора у цьому базисі пишуть .

Приклад. Дано: , , .

Перевірити чи утворюють дані вектори базис. Якщо так, то знайти координати вектора в цьому базисі.

1. знайдемо мішаний добуток даних векторів:

, значить дані вектори некомпланарні, тобто утворюють базис.

2. Виразимо вектор через вектори , , :

Складаємо систему рівнянь  ; ;

Отже ,