Однорідні системи лінійних рівнянь.

Системи лінійних рівнянь називаються однорідними, якщо праві частини рівнянь дорівнюють нулю.

Однорідна система m лінійних рівнянь з п невідомими має вигляд:

Ця система завжди має нульовий розв’язок: .

Ненульовий розв’язок даної системи (якщо він є) можна знайти методом Гаусса. Якщо і визначник  системи дорівнює нулю (=0), то однорідна система має безліч ненульових розв’язків.

Нехай дано систему двох однорідних лінійних рівнянь з трьома невідомими

Розв’язок такої системи можна знайти за формулами

, , , де - довільне число.

Нехай дано систему трьох однорідних лінійних рівнянь з трьома невідомими

Якщо 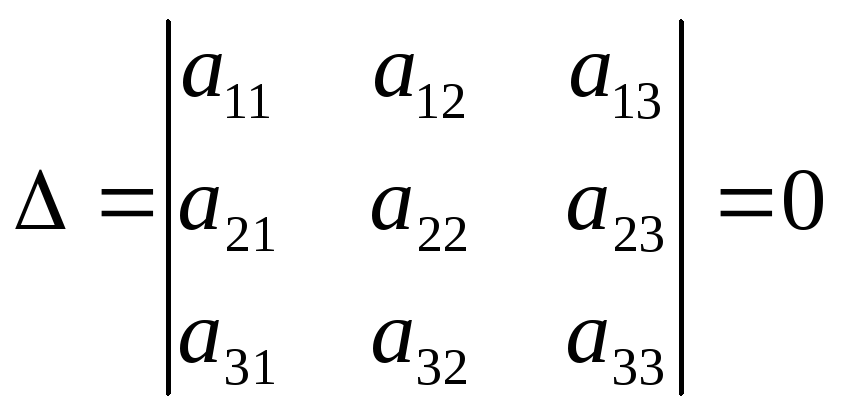, то система має безліч розв’язків. Нехай у визначнику  існує принаймні один відмінний від нуля мінор другого порядку, наприклад, , тоді розв’язки можна знайти за формулами , , , де - довільне число.

Приклад. Розв’язати систему лінійних однорідних рівнянь

,

Відповідь:

Контрольні запитання.

1. Що називається матрицею? Назвіть їх види.

2. Що називається визначником, мінором визначника, алгебраїчним доповненням ?

3. Назвіть основні властивості визначників?

4. Сформулюйте методи обчислення визначників і поясніть їх суть.

5. Які дії можна виконувати над матрицями? Покажіть на прикладах.

6. Як знайти обернену матрицю?

7. Сформулюйте методи розв’язування систем лінійних алгебраїчних рівнянь? Поясніть їх суть.

8. Що називається рангом матриці? Як його знайти?

9. Яка система рівнянь називається однорідною? Як знайти її розв’язки?

Література.

А.П.Рябушко, В.В. Бархатов, В.В.Державець, І.Є. Юруть. Збірник індивідуальних завдань з вищої математики. Розділ 1

Векторна алгебра.

План.

1. Лінійні операції над векторами.

2. Скалярний добуток векторів.

3. Векторний добуток векторів.

4. Мішаний добуток векторів.

5. Базис.

6. Ділення відрізка у даному відношенні.

Лінійні операції над векторами.

Скалярні величини характеризуються числовим значенням: маса, час і т.д.

Векторні величини характеризуються числовим значенням і напрямом: швидкість, сила і т.д.

В

В

ектор – це напрямлений відрізок: , точка А – початок вектора, точка В – кінець вектора.

А

Нульовий вектор – це вектор, у якого початок і кінець співпадають: .

Довжина вектора (модуль, абсолютна величина) - це довжина відрізка, який зображає даний вектор: .

Вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.

Два вектори називаються рівними, якщо вони колінеарні, однаково напрямлені та рівні по довжині.

Дії над векторами в геометричній формі.

1. Добутком вектора на число називається вектор, модуль якого дорівнює 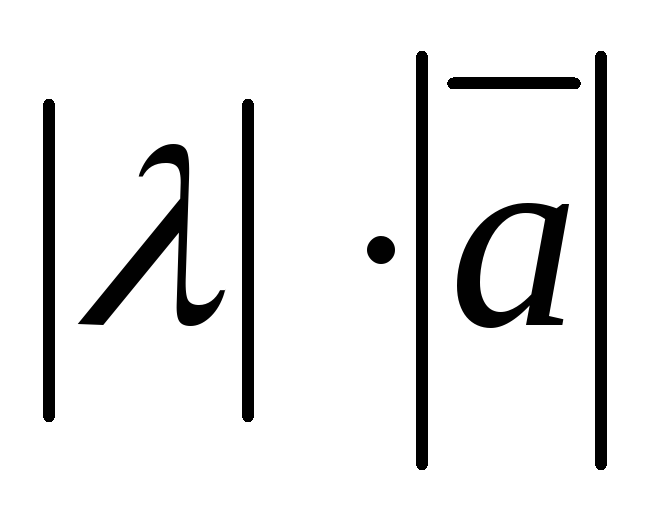, а напрям співпадає з напрямом вектора , якщо 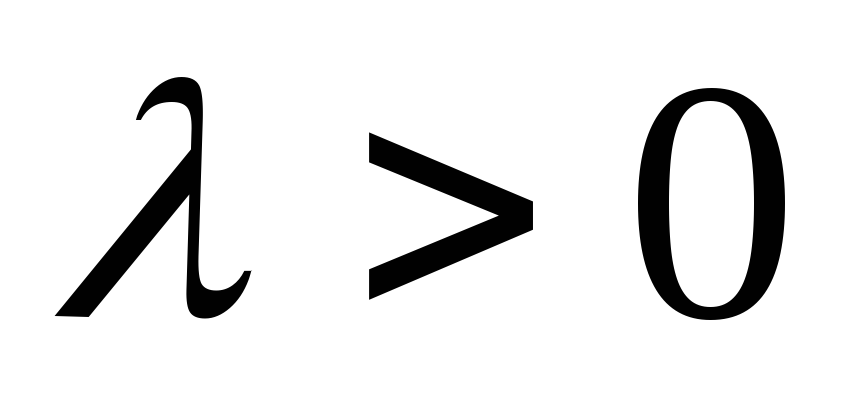і протилежний напряму , якщо .

2. додавання векторів:

• правило трикутника:

- правило паралелограма:

3. віднімання векторів:

Координатами вектора називаються його проекції на осі координат.

, де - одиничні вектори, орти.

Якщо і , то координати вектора знаходяться за формулою: (якщо , то ).

Рівні вектори мають рівні координати.

Довжина вектора: , (якщо , то )..

Якщо вектори і колінеарні, то їх координати пропорційні .