Інтеграл та його застосування

План.

10. Первісна та невизначений інтеграл.

11. Основні властивості невизначеного інтеграла.

12. Таблиця невизначених інтегралів.

13. Методи знаходження невизначених інтегралів.

14. Визначений інтеграл.

15. Властивості визначеного інтеграла.

16. Методи розв’язування систем лінійних рівнянь.

17. Ранг матриці.

18. Однорідні системи. Первісна та невизначений інтеграл.

В багатьох практичних задачах необхідно по заданій похідній відновити первісну функцію.

Означення. Функція F(x) називається первісною для функції f(x) на проміжку (а; b), , якщо на цьому проміжку .

Операція знаходження первісних для функції f(x) називається інтегруванням f(x).

Означення.Невизначеним інтегралом для неперервної функції називають множину всіх первісних функцій і позначають

де:

— знак невизначеного інтеграла;

f(x) — підінтегральна функція;

f(x) dx — підінтегральний вираз;

dx — диференціал змінної інтегрування.

Основні властивості невизначеного інтеграла.

1) ;

2) ;

3) .

Таблиця невизначених інтегралів.

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

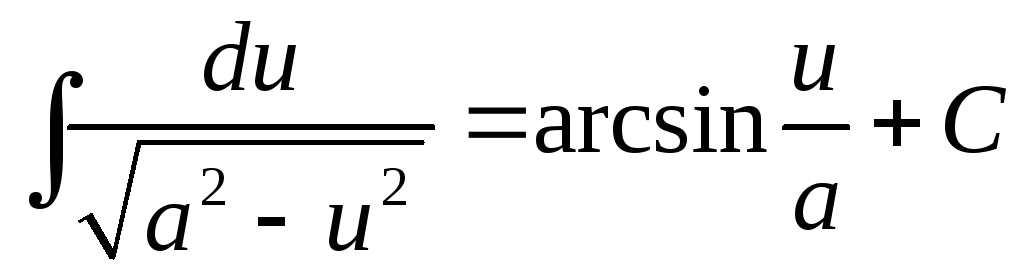15. ;

16. ;

17..

Методи знаходження невизначених інтегралів.

Під час знаходження невизначених інтегралів застосовують такі способи: безпосереднє інтегрування, метод підстановки, інтегрування частинами, інші.

Інтегрування розкладанням: мета методу — розкласти підінтегральну функцію на такі доданки, інтеграли від яких відомі або їх простіше інтегрувати, ніж початкову підінтегральну функцію.

Приклад. Знайти інтеграл .

Виділимо цілу частину підінтегральної функції. Для цього поділимо чисельник на знаменник способом ділення многочлена на многочлен, або припишемо в чисельнику та і розглянемо суму дробів. Одержимо

.

.

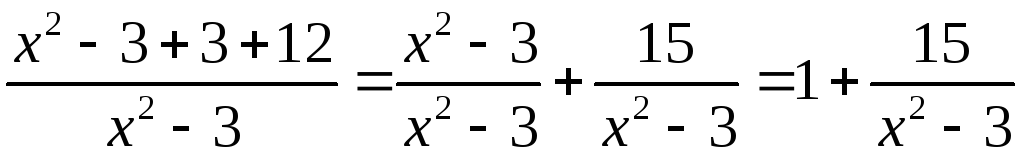Приклад. Знайти інтеграл .

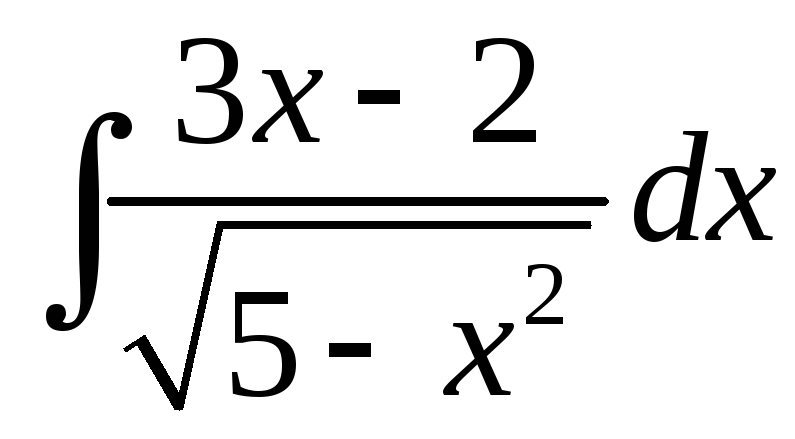Розглянемо різницю двох інтегралів і до кожного із них застосуємо відповідну формулу із таблиці інтегралів. Одержимо

,

.

Приклад. Знайти інтеграл .

Виділимо повний квадрат у знаменнику підінтегральної функції і зможемо застосувати відповідну формулу із таблиці інтегралів. Одержимо:

Метод підстановки: мета методу підстановки — перетворити даний інтеграл до такого вигляду, який простіше інтегрувати.

Приклад. Знайти інтеграл .

Часто доводиться вводити заміну для спрощення обчислення інтегралу. Замінимо на нову змінну. Одержимо

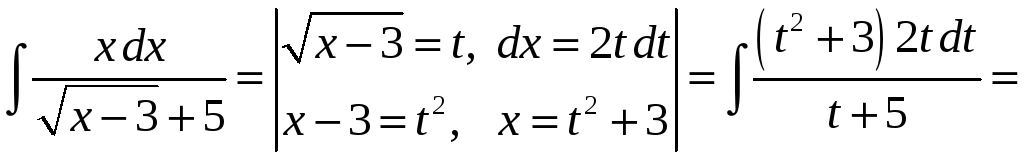
У цьому випадку було застосовано ділення:

Інтегрування частинами: мета методу – застосувати один чи декілька разів формулу для знаходження інтегралу:

Приклад. Знайти інтеграл .

Приклад. Знайти інтеграл .

Одержимо:

Визначений інтеграл.

Означення. Криволінійною трапецією називається плоска фігура, що обмежена лініями:

На малюнку зображені: класична криволінійна трапеція та її окремі випадки.

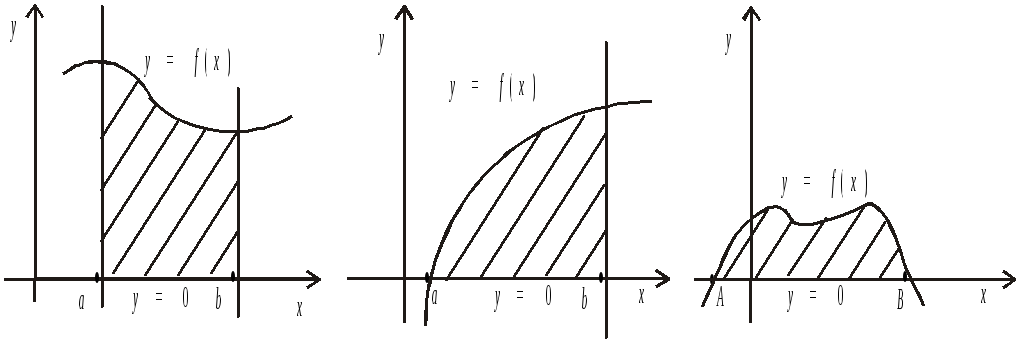
Обчислення площі криволінійної трапеції приводить до розгляду нового математичного поняття – визначеного інтегралу, який позначається:

де:

— знак визначеного інтеграла;

а, b — нижня та верхня межі інтегрування;

f(x) — підінтегральна функція;

f(x) dx — підінтегральний вираз;

dx — диференціал змінної інтегрування.

Якщо , то дорівнює площі відповідної криволінійної трапеції.