Содержание стр.
Введение………………………………2
1. Каналы сбыта…………………………..4
2. Охват рынка……………………………28
3. Объем закупок (поставок)…………….50
4. Товародвижение………………………..52
Список литературы…………………105
Введение.
Сбыт – это движение товара от производителя до конечного потребителя и пользователя. Он является неотъемлемым элементом процесса маркетинга, так как представляет собой завершающую, наиболее ответственную стадию обеспечения потребителя необходимым ему товаром. Сбыт направлен на формирование и поддержание эффективной системы перемещения продукта от производителя до потребителя с минимальными затратами. Система сбыта функционирует под влиянием значительного количества факторов внешней среды, которые оказывают отрицательное воздействие на экономические показатели этой системы. Поэтому имеется объективная необходимость организации непрерывного контроля над функционированием всех элементов системы сбыта с целью выявления и профилактики возможных отклонений в экономическом поведении сбытовых организаций и достижения поставленных целей.
При принятии решений в целях осуществления мероприятий сбытовой политики применяются: величина товарооборота, доля рынка, расходы по сбыту, степень разветвленности сбытовой сети, имидж каналов сбыта, наличие сбытовых посредников и партнеров, организация и контроллинг сбыта и т.д. От правильности принятых решений зависит и текущее состояние дел в организации, и степень устойчивости фирмы на рынке в целом, что налагает огромную ответственность на ЛПР (лицо, принимающее решения) и предъявляет к нему высокие требования в части теоретической и особенно практической подготовки. На сегодняшний день уровень квалификации специалистов в данной области создается в основном за счет теоретической подготовки. Недостаток практических материалов сказывается не только на процессе обучения и усвоения каждой дисциплины курса, но и на работе маркетолога любого предприятия в дальнейшем. Целью данного сборника является обобщение некоторого практического материала по различным аспектам сбытовой политики (оценка эффективности каналов сбыта, выбор каналов товародвижения, посредники, объем закупок, привлекательность рынков, стратегия снабжения и т.п.), который будет полезен студентам, специалистам по маркетингу, экономистам при решении аналогичных задач.
1. Каналы сбыта Пример 1.
Необходимо провести маркетинговое исследование для сбыта продукции (йогурт); узнать, сколько его нужно поставить в конкретный район города, целесообразно ли это делать вообще. Одна из проблем состоит в том, что в одном из районов неизвестно потребление данной продукции Также необходимо определить долю потребителей с определенным доходом (например, до 1000 руб в месяц на члена семей ) и проверить гипотезу о нормальном распределении дохода среди потребителей района «А»
Вначале определим емкость рынка. Емкость рынка – это то количество йогурта, которое потребители готовы потребить. Чтобы найти емкость рынка в районе, надо найти среднее потребление в районе по выборочной совокупности, перенести её на генеральную с учетом ошибки и перемножив среднюю и количество населения в районе, получить емкость рынка по данной продукции.
Вычислим среднее потребление йогурта в первом районе, как взвешенную (вес-количество человек):
Таблица 1.1.
Расчетные данные
Потребление йогурта населением,кг |
Количество человек в выборке |
0,1 |
35 |
0,2 |
21 |
0,4 |
22 |
0,8 |
21 |
0,9 |
11 |
Итого |
110 |
Дисперсия по выборочной совокупности:
S
Так как выборочное наблюдение велось бесповторным методом, то средняя квадратическая ошибка средней рассчитывается с корректировкой на бесповторность, т.е.
S
=
,где
-дисперсия
признака по генеральной совокупности
N- Объем генеральной совокупности
n- Объем выборочной совокупности
Так как выборочная
совокупность большая(>100), то в формуле
можно заменить генеральную дисперсию(
)
на выборочную(S
)
S
Возьмем коэффициент
доверия t=1,96
(доверительная вероятность F=0,95)/Тогда
предельная ошибка ∆
=t
Среднее потребление
йогурта
в первом районе будет находиться в
интервалах:
Если
каждую границу доверительного интервала
среднего потребления умножить на
количество N
человек
в районе i
, то получим границы доверительного
интервала емкости Е рынка по данной
продукции (в кг): N(
В нашем случае
0,3927 – 0б0568≤
или
0,3359
,
тогда при N=100
тыс.жителей емкость рынка E
йогуртов составит диапазон 33590≤E≤44590кг
Для того, чтобы узнать емкость рынка в районе «В» ,необходимо перенести среднее потребление из района «А» в район»В» и найти в последнем ошибку средней в соответствии с теми признаками, которые оказывали влияние на потребление.
Построим для каждого описательного признака корреляционную таблицу, которая уже при общем знакомстве может дать возможность выдвинуть предположение о наличии или отсутствии связи, а также её направление.
Построение корреляционной таблицы начнем с группировки значений её факторного и результативного признаков. Так как они представлены всего пятью вариантами повторяющихся значений, то достаточно просто выписать эти значения.
Для получения обобщающего показателя , характеризующего тесноту связи между качественными признаками и позволяющего сравнить проявление связи в разных совокупностях , исчисляют коэффициент Пирсона (С) или Чупрова (К):
С=
К=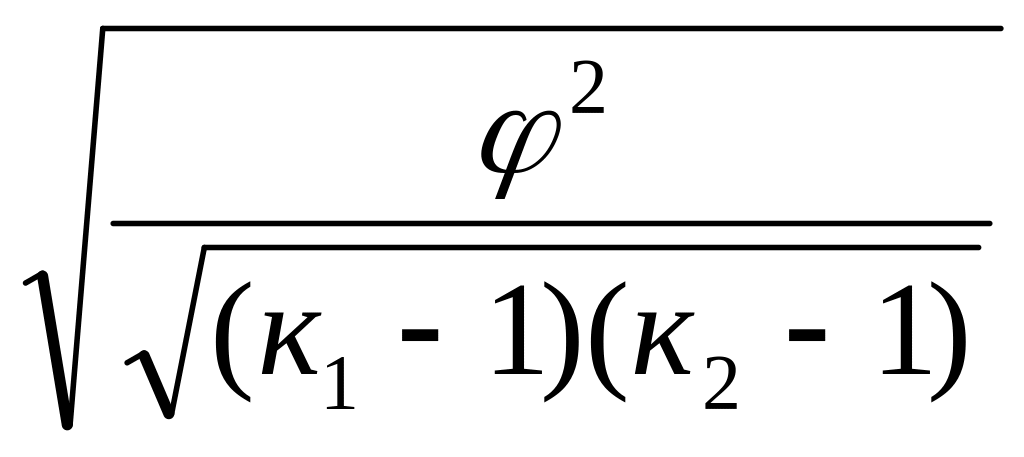
Где
-
показатель средней квадратической
сопряженности, определяемой путем
вычитания единицы из суммы отношений
квадратов частот каждой клетки
корреляционной таблицы к произведению
частот соответствующего столбца и
строки:
f
f
К1, к2-число групп по каждому из признаков
Величина этих коэффициентов колеблется в пределах от 0 до 1 , но для того, чтобы принять связь за существенную, необходимо, чтобы С,К>0,3
Таблица.1.2.
Распределение потребителей по полу и потреблению йогуртов.
Группы потребителей по полу |
Группы потребителей по потреблению йогуртов, кг\мес. |
Итого |
||||
0,1 |
0,2 |
0,4 |
0,8 |
Более 0,8 |
||
1 |
2 |
3 |
4 |
5 |
6 |
|
Женщины |
17 |
8 |
10 |
9 |
10 |
54 |
Мужчины |
18 |
13 |
12 |
12 |
1 |
56 |
Итого |
35 |
21 |
22 |
21 |
11 |
110 |
К=
Исходя из результатов данных, связь между потреблением йогурта и полом несущественная.
Таблица 1.3
Распределение потребителей по роду занятий и потреблению йогуртов
Группы потребителей по роду занятий |
Группы потребителей по потреблению йогуртов ,кг\мес |
Итого |
||||
0,1 |
0,2 |
0,4 |
0,8 |
Более 0,8 |
||
А |
1 |
2 |
3 |
4 |
5 |
6 |
Учащийся |
1 |
1 |
1 |
- |
- |
3 |
Студент |
2 |
1 |
- |
- |
- |
3 |
Служащий |
11 |
5 |
14 |
7 |
1 |
38 |
Рабочий |
13 |
8 |
5 |
7 |
5 |
38 |
Предприниматель |
8 |
6 |
2 |
7 |
5 |
28 |
Итого |
35 |
21 |
22 |
21 |
11 |
110 |
С=
Из значения коэффициента Чупрова можно сделать вывод о том, что связь между потреблением йогурта и родом занятий существенна.
Таблица 1.4.
Распределение потребителей по образованию и потреблению йогуртов
Группы потребителей по образованию |
Группы потребителей по потреблению йогуртов ,кг\мес |
Итого |
||||
0,1 |
0,2 |
0,4 |
0,8 |
Более 0,8 |
||
А |
1 |
2 |
3 |
4 |
5 |
6 |
Нет |
1 |
1 |
1 |
- |
- |
3 |
Среднее |
5 |
7 |
3 |
1 |
1 |
17 |
Ср.-спец. |
15 |
7 |
9 |
6 |
3 |
40 |
н\высшее |
5 |
3 |
- |
5 |
1 |
14 |
высшее |
9 |
3 |
9 |
9 |
6 |
36 |
Итого |
35 |
21 |
22 |
21 |
11 |
110 |
С=
Вывод: связь между потреблением йогурта и образованием существенна
Рассмотрим выявление зависимости потребления йогурта от количественных признаков .Для предварительного выявления наличия связи и раскрытия её характера можно применить графический метод. Используя данные об индивидуальных значениях признака-фактора и соответствующих ему значениях результативного признака, можно построить в прямоугольных координатах точечный график («поле корреляции»)
Построим также для каждого количественного признака корреляционную таблицу. Для факторного признака необходимо определить величину интервала .Для этого воспользуемся формулой Стэрджесса:
Для доли питания:
h=
Таблица 1.5.
Распределение потребителей по доле питания и потреблению йогуртов
Группы потребителей по доле питания, % |
Группы потребителей по потреблению йогуртов ,кг\мес |
Итого |
||||
0,1 |
0,2 |
0,4 |
0,8 |
Более 0,8 |
||
А |
1 |
2 |
3 |
4 |
5 |
6 |
Менее 42 |
2 |
6 |
1 |
3 |
2 |
14 |
42-44 |
7 |
1 |
2 |
4 |
2 |
16 |
44-46 |
6 |
1 |
8 |
3 |
1 |
19 |
46-48 |
7 |
2 |
2 |
3 |
1 |
15 |
48-50 |
4 |
3 |
2 |
3 |
1 |
13 |
50-52 |
2 |
4 |
1 |
4 |
- |
11 |
52-54 |
7 |
1 |
4 |
- |
1 |
13 |
Более 54 |
- |
3 |
2 |
1 |
3 |
9 |
Итого |
35 |
21 |
22 |
21 |
11 |
110 |
В отличии от предыдущей таблицы в следующих взяты интервалы 10,1000, 5 для более простой трактовки данных.
Таблица 1.6.
Распределение потребителей по возрасту и потреблению йогуртов
Группы потребителей по возрасту, лет |
Группы потребителей по потреблению йогуртов ,кг\мес |
Итого |
||||
0,1 |
0,2 |
0,4 |
0,8 |
Более 0,8 |
||
А |
1 |
2 |
3 |
4 |
5 |
6 |
Менее 20 |
3 |
3 |
2 |
1 |
2 |
11 |
20-30 |
14 |
10 |
7 |
10 |
5 |
46 |
30-40 |
12 |
3 |
5 |
12 |
3 |
35 |
40-50 |
2 |
5 |
- |
2 |
1 |
10 |
50-60 |
3 |
- |
- |
1 |
- |
4 |
Более 60 |
1 |
- |
1 |
2 |
- |
4 |
Итого |
35 |
21 |
22 |
21 |
11 |
110 |
Таблица 1.7.
Распределение потребителей по доходу и потреблению йогуртов
Группы потребителей по доходу,руб. |
Группы потребителей по потреблению йогуртов ,кг\мес |
Итого |
||||
0,1 |
0,2 |
0,4 |
0,8 |
Более 0,8 |
||
А |
1 |
2 |
3 |
4 |
5 |
6 |
Менее 1000 |
15 |
5 |
9 |
- |
- |
29 |
1000-2000 |
9 |
8 |
9 |
13 |
5 |
44 |
2000-3000 |
6 |
2 |
3 |
2 |
3 |
16 |
3000-4000 |
1 |
3 |
- |
3 |
3 |
10 |
4000-5000 |
3 |
1 |
- |
2 |
- |
6 |
Более 5000 |
1 |
2 |
1 |
1 |
- |
5 |
Итого |
35 |
21 |
22 |
21 |
11 |
110 |
Из таблиц можно
сделать вывод о том, что потребление не
связано линейной зависимостью с
каким-либо количественным признаком.
Поэтому оценить связь между этими
признаками можно лишь с помощью
эмпирического корреляционного отношения
:
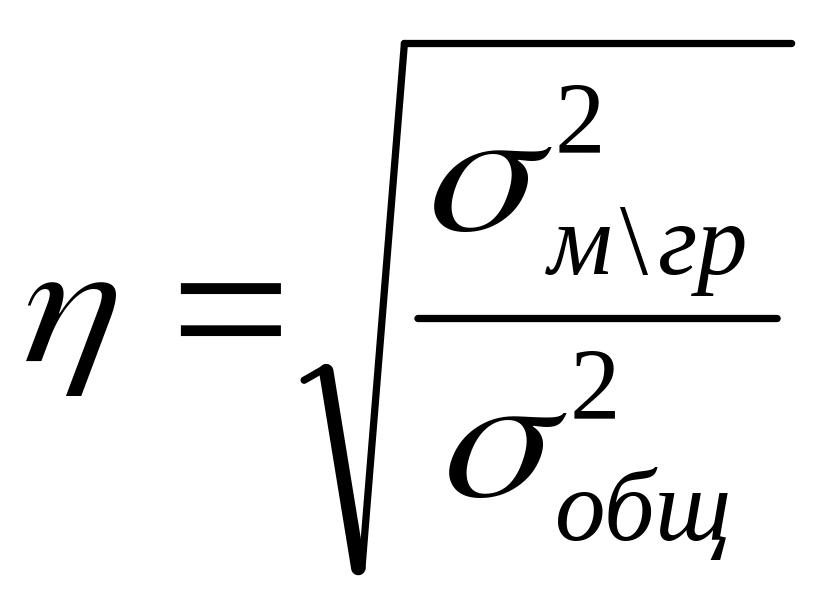
Таблица 1.8.
Расчет корреляционного отношения для дохода:
Потребление |
Кол-во человек |
Средний доход |
( |
0,1 |
35 |
1665,80 |
1949360,00 |
0,2 |
21 |
2141,00 |
1201549,44 |
0,4 |
22 |
1482,64 |
3865359,39 |
0,8 |
21 |
2389,95 |
5004147,69 |
0,9 |
11 |
2102,45 |
442884,71 |
Итого |
110 |
1901,80 |
12463301,23 |
Средний доход по
группе:
Межгрупповая
дисперсия:
Общая дисперсия:
Корреляционное
отношение:
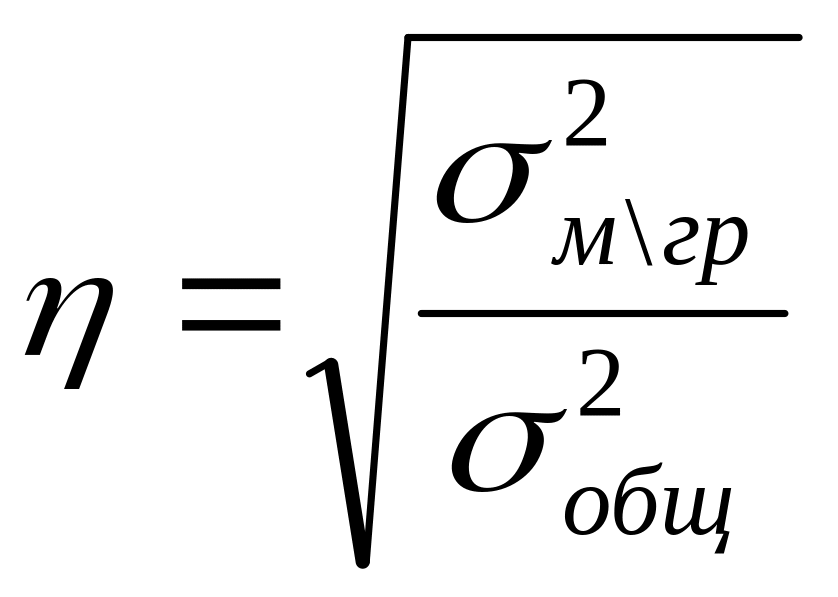=0,250
Таблица 1.9.
Расчет корреляционного отношения для возраста:
Потребление |
Кол-во человек |
Средний возраст |
( |
0,1 |
35 |
32,06 |
43,97 |
0,2 |
21 |
29,14 |
67,55 |
0,4 |
22 |
30,50 |
4,19 |
0,8 |
21 |
33,48 |
135,47 |
0,9 |
11 |
26,82 |
186,55 |
Итого |
110 |
30,94 |
437,72 |
Средний доход по
группе:
Межгрупповая
дисперсия:
Общая дисперсия:
Корреляционное отношение: =0,180
Расчет корреляционного отношения для доли питания (в отличие от возраста и дохода средняя и общая дисперсия взвешиваются доходом, т.к. доли- вторичный признак):
Таблица 1.10
Расчет корреляционного отношения для доли питания
Потребление |
Кол-во человек |
Средняя доля питания |
( |
0,1 |
35 |
46,56 |
12,90 |
0,2 |
21 |
47,88 |
10,62 |
0,4 |
22 |
46,99 |
0,74 |
0,8 |
21 |
47,61 |
4,04 |
0,9 |
11 |
46,63 |
3,27 |
Итого |
110 |
47,17 |
31,57 |
q
-вес
–доход , f
-количество
человек
Средний доход по
группе:
Межгрупповая
дисперсия:
Общая дисперсия:
Корреляционное отношение: =0,123
Для существенности
связи факторного и результативного
признаков надо, чтобы выполнялось
следующее условие:
В
данном случае ни одно корреляционное
отношение не превышает даже 0,3.
следовательно, связи несущественны.
Если какая-нибудь связь была бы существенна, следовало бы построить уравнение регрессии, а перед этим определить тип зависимости (например, y=a+bx- линейная зависимость)Для точного определения параметров а и b уравнения регрессии используется метод наименьших квадратов. При применении метода наименьших квадратов для нахождения такой функции , которая наилучшим образом соответствует эмпирическим данным, считается, что сумма квадратов отклонений эмпирических точек теоретической линии регрессии должна быть величиной минимальной.
Критерий метода наименьших квадратов можно записать таким образом:
S=
Поскольку не все
фактические значения признака лежат
на линии регрессии, более справедливо
для записи уравнения корреляционной
зависимости воспользоваться формулой
y=a+bx+e,где
е отражает случайную составляющую
вариации результативного признака. Для
всей совокупности наблюдаемого значения
рассчитывается средняя квадратическая
ошибка уравнения регрессии S
,
которая представляет собой среднее
квадратическое отклонение фактических
значений y
относительно значений ,рассчитанных
по уравнению регрессии
,
т.е.
S
,где
S
-
средняя квадратическая ошибка уравнения
регрессии;
y - фактические значения результативного признака, полученные по данным наблюдения;
-значения результативного признака, рассчитанные по уравнению корреляционной связи и полученные подстановкой значений факторного признака x в уравнение регрессии y=a+bx;
m-число параметров в уравнении регрессии;
В данной формуле сумма квадратов отклонений y от делится на число степеней свободы в оценке теоретических значений результативного признака по уравнению регрессии с m параметрами. В случае линейного уравнения регрессии m=2.
Чем меньше рассеяние эмпирических точек вокруг прямой, тем меньше средняя квадратическая ошибка уравнения .Таким образом, величина S служит показателем значимости и полезности прямой, выражающей соотношение между двумя признаками.
Средняя кадратическая ошибка уравнения дает возможность в каждом отдельном случае с определенной вероятностью указать, что величина результативного признака окажется в определенном интервале относительно значения, вычисленного по уравнению связи.
Определим доверительные границы для результативного признака, т.е. те границы, в пределах которых с заданной доверительной вероятностью будет находиться теоретическое значение y. Поскольку параметры уравнения регрессии определяются по выборочным данным, являясь функцией наблюдаемых значений , оценки параметров a и b содержат некоторую погрешность. Дисперсия значения зависимой переменной , определяемой по уравнению линейной зависимости, будет складываться из дисперсии параметра а и дисперсии параметра b.
Зная дисперсию
показателя
и задаваясь уравнением доверительной
вероятности, можно определить доверительные
границы результативного признака при
значении факторного признака x
следующим образом:
y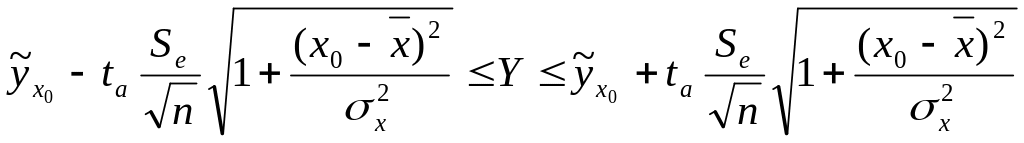
где t
определяется
в соответствии с уровнем значимости по
t-распределению
Стьюдента
Величина множителя
C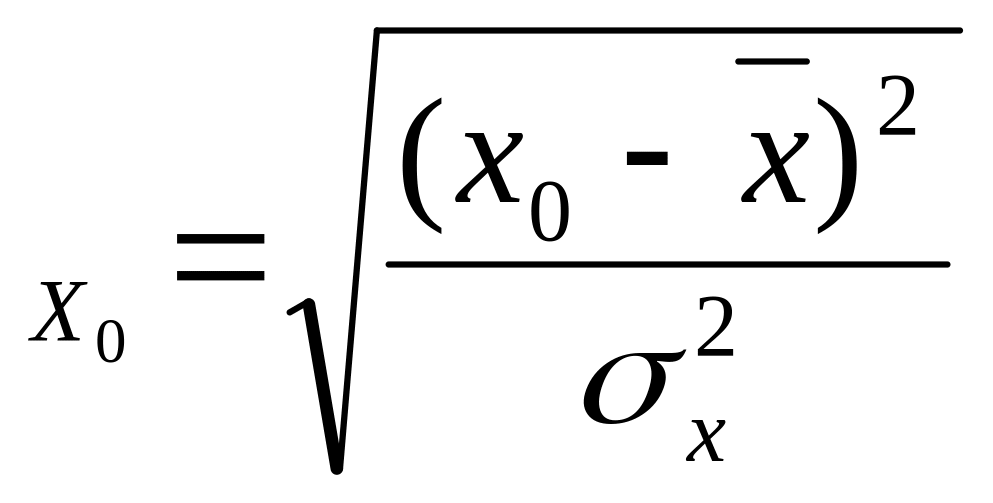
будет вычисляться для каждого значения
x
C
удалением значения факторного признака
от своего среднего арифметического
значения величина С
будет
возрастать.
Поскольку параметры уравнения регрессии определяются по выборочным данным, являясь функцией наблюденных значений, оценки параметров a и b содержат некоторую погрешность. Поэтому, как и во всех случаях оценки параметров генеральной совокупности по выборочным данным, возникает задача проверки гипотезы о величине коэффициента регрессии.
Рассмотрим перенесение среднего потребления на район «А».Построим сложную группировку по признакам, у которых связь с потреблением существенна (род занятий и образование).Найдем среднее потребление в каждой группе и перенесем его в соответствующую группу во второй район. Коэффициент доверия в группе надо находить по таблице Стьюдента , так как каждая группа представляет собой малую выборку. После этого необходимо найти предельную ошибку в каждой группе потребителей:
Где S -средняя ошибка из первого района, t=1,96
И рассчитать предельную ошибку средней всего района в целом (как взвешенную среднюю, у которой вес-количество человек в группе):
Тогда среднее потребление во втором районе находится в интервале:
;
0,3927-0,0698≤
;
0,3229
Если каждую границу доверительного интервала среднего потребления умножить на количество человек в районе (100000 чел.) то получим границы доверительного интервала емкости рынка по данной продукции (в кг):
32290
Проведем расчет доли p потребителей с доходом до 1000 руб \мес на члена семьи в районе «В»:
p=
Доверительные пределы генеральной доли выглядят так:
p
- t
Величина
доверительного интервала для генеральной
доли зависит от величины предельной
ошибки выборки
Чем
больше величина предельной ошибки
выборки, тем больше величина доверительного
интервала и тем ниже точность оценки.
Поскольку величина предельной ошибки выборки равна t , то точность оценки параметров генеральной совокупности будет зависеть от принятого уровня доверительной вероятности и от величины стандартной ошибки выборки.
Средняя ошибка доли для бесповторной выборки:
S
С вероятностью
F=0,95
можем утверждать , что предельная ошибка
доли потребителей с доходом до 1000
руб\мес. в первом районе не превысит
0,0823 (
)
и доля этих потребителей в генеральной
совокупности будет находиться в
интревале: 0,1817
Рассмотрим проверку гипотезы о нормальном распределении показателя «среднемесячный доход» в районе «В»
Степень расхождения теоретических и эмпирических частот оценивается с помощью особых показателей – критериев согласия, с помощью которых проверяется гипотеза о законе распределения. Критерии согласия основаны на использовании различных мер расстояний между анализируемым эмпирическим распределением и функцией распределения признака в генеральной совокупности.
Одним из наиболее
часто употребляемых критериев согласия
является критерий «хи-квадрат» (
),
предложенный К.Пирсоном:
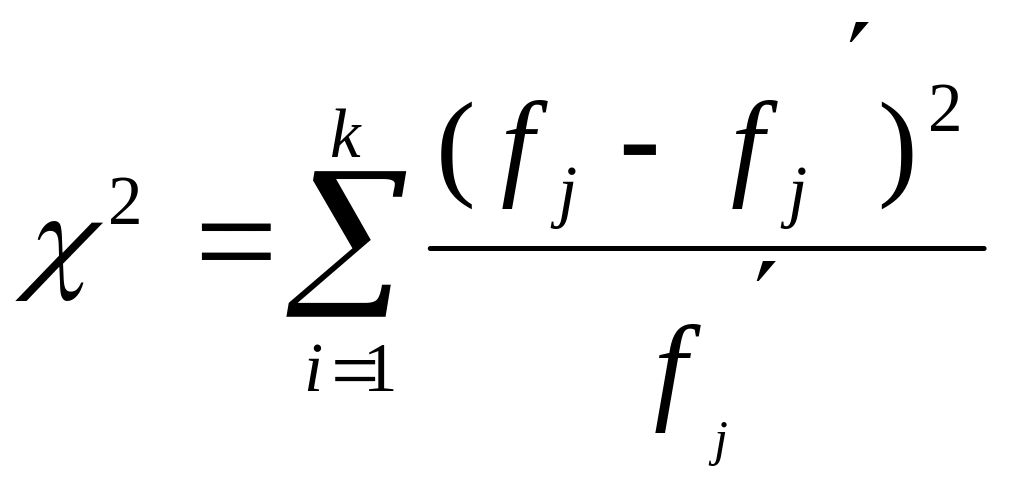
Где f
и
-
соответственно частот эмпирического
и теоретического распределения в j-ом
интервале.
Чем больше разность
между наблюдаемыми и теоретическими
частотами, тем больше величина критерия
Пирсона. Чтобы отличить существенные
значения
от
значений , которые могут возникнуть в
результате случайностей выборки,
рассчитанное значение критерия
сравнивается с табличным значением
при соответствующем числе степеней
свободы и заданном уровне значимости.
Уровень значимости выбираем таким
образом, чтоP(
>
)=a
(величина а принимается равной 0,05 или
0,01)
Определив значение критерия Пирсона по данным конкретной выборки, можно встретиться с такими вариантами:
1) > , т.е. попадает в критическую область .Это означает, что расхождение между эмпирическими и теоретическими частотами существенно и его нельзя объяснить случайными колебаниями выборочных данных В таком случае гипотеза о близости эмпирического распределения к нормальному отвергается.
2) ≤ , т.е.рассчитанный критерий не превышает максимально возможную величину расхождения эмпирических и теоретических частот ,которая может возникнуть в силу случайных колебаний выборочных данных. В этом случае гипотеза о близости эмпирического распределения к нормальному не отвергается.
Табличное значение критерия Пирсона определяется при фиксированном уровне значимости и соответствующем числе степеней свободы.
Число степеней свободы равно k-l-1,где l- число условий, которые предполагаются выполненными при вычислении теоретических частот, k –число групп
Так при вычислении теоретических частот нормального распределения в качестве оценок генеральной средней и дисперсии используются соответствующие выборочные характеристики , то для проверки гипотезы о нормальности распределения число степеней свободы равно (k-3)
При расчете критерия Пирсона нужно соблюдать следующие условия:
число наблюдений должно быть достаточно велико, во всяком случае n≥50;
если теоретические частоты в некоторых интервалах меньше 5, то такие интервалы объединяют так, чтобы частоты были более 5
Расчеты по вычислению приведены в таблице 1.1.11
Таблица 1.11
Расчеты по вычислению
Доход |
|
f |
* f |
|
|
f(t) |
|
Менее 960 |
605 |
26 |
15730 |
44639038,34 |
-1,00847 |
0,2399 |
14 |
960-1670 |
1315 |
34 |
44710 |
12252243,06 |
-0,46202 |
0,3586 |
22 |
1670-2380 |
2025 |
23 |
46575 |
276784,07 |
0,08443 |
0.3975 |
24 |
2380-3090 |
2735 |
9 |
24615 |
6047172,81 |
0,63087 |
0,3270 |
20 |
3090-3800 |
3445 |
6 |
20670 |
14039892,54 |
1,17732 |
0,1995 |
12 |
3800-4510 |
4155 |
4 |
16620 |
20065024,36 |
1,72377 |
0,0903 |
6 |
4510-5220 |
4865 |
4 |
19460 |
34802920,36 |
2,27022 |
0,0303 |
2 |
БОЛЕЕ 5220 |
5575 |
4 |
22300 |
53573616,36 |
2,81667 |
0,0076 |
0 |
|
|
110 |
210680 |
185696691,90 |
|
|
|
Где -середина интервала;
f -количество человек в группе
t-нормативное отклонение;
f(t)=
-нормативная функция;
- теоретическая
частота;
Средний доход:
Среднеквадратическое:
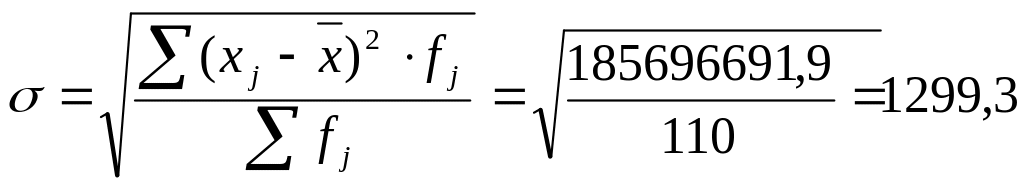
Объединив интервалы 6-8, получаем следующие данные:
Таблица 1.12
Номер интервала |
Эмпирические частоты |
Теоретические частоты |
( |
1 |
26 |
14 |
9,300 |
2 |
35 |
22 |
7,189 |
3 |
23 |
24 |
0,034 |
4 |
9 |
20 |
5,774 |
5 |
6 |
12 |
2.993 |
6 |
12 |
8 |
2,000 |
Итого |
|
|
27,284 |
Критерий Пирсона
(фактический):
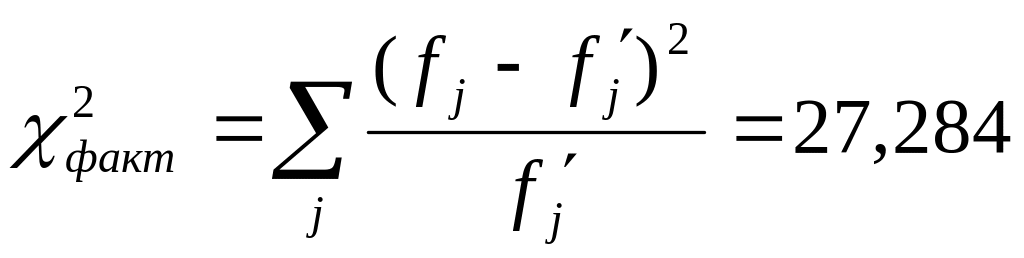
Критерий Пирсона
(табличный):
Так как
>
,
то не подтверждается гипотеза о нормальном
распределении показателя «среднемесячный
доход потребителя» в районе «В»