
- •Содержание
- •2. Виды самостоятельной работы студентов по дисциплине
- •3. Рекомендации по организации самостоятельной работы студентов по темам дисциплины Тема 1. Введение. Предмет теории оптимальных решений. Люди и их роли в принятии решений. Альтернативы, критерии
- •1) Самостоятельное изучение теоретического материала по теме:
- •2) Вопросы для самоконтроля:
- •Тема 2. Исследование операций и его роль в принятии решений. Этапы операционного исследования и их содержание. Математическая модель и её виды. Классы операционных задач
- •Тема 3. Классические методы оптимизации. Одномерная безусловная и условная оптимизации. Многомерная безусловная и условная оптимизации
- •Часть 1. Классические методы оптимизации: Одномерная безусловная и условная оптимизации.
- •§1. Классические методы оптимизации.
- •Часть 2. Классические методы оптимизации: многомерная безусловная и условная оптимизации.
- •1) Изучение теоретического материала по теме:
- •§1. Классические методы оптимизации.
- •3) Самостоятельное решение примеров:
- •4) Вопросы для самоконтроля:
- •Тема 4. Общая теория многомерной безусловной и условной оптимизации
- •Часть 1. Многомерная безусловная оптимизация.
- •§2. Безусловный экстремум функций нескольких переменных.
- •Часть 2. Многомерная условная оптимизация.
- •§3. Условный экстремум функций нескольких переменных.
- •3) Самостоятельное решение примеров:
- •4) Вопросы для самоконтроля:
- •Тема 5. Численные методы безусловной оптимизации
- •Часть 1. Общие положения. Методы нулевого порядка.
- •§1. Общие положения.
- •§2. Методы нулевого порядка одномерной минимизации.
- •Часть 2. Методы первого и второго порядка.
- •§3. Методы первого и второго порядка.
- •Тема 6. Элементы численных методов задачи условной оптимизации выпуклого программирования
- •§4. Элементы численных методов задачи условной оптимизации выпуклого программирования.
- •Тема 7. Постановка задачи динамического программирования. Принцип оптимальности и уравнения Беллмана. Задача распределения ресурсов
- •§1. Общая постановка задачи динамического программировании.
- •§2. Принцип оптимальности и уравнения Беллмана.
- •§3. Задача о распределении средств между предприятиями.
- •Тема 8. Общая схема применения метода динамического программирования. Задачи замены оборудования и прокладки трубопровода
- •§4. Общая схема применения метода дп. Задача об оптимальном распределении ресурсов между отраслями на n лет.
- •§5. Задача о замене оборудования.
- •§6. Задача прокладки трубопровода.
- •Тема 9. Задача линейного программирования злп)
- •§1. Задача линейного программирования. Типичные задачи линейного программирования, их математические модели.
- •§2. Общая злп. Канонический злп.
- •§3. Теоретические основы решения злп. Геометрическая интерпретация злп. Идея аналитического решения.
- •3) Самостоятельное решение примеров:
- •4) Вопросы для самоконтроля:
- •Тема 10. Симплекс-метод решения задачи линейного программирования
- •§3. Теоретические основы решения злп. Геометрическая интерпретация злп. Идея аналитического решения.
- •§4. Симплекс-метод решения злп.
- •Тема 11. Метод искусственного базиса. Целочисленная злп
- •Тема 12. Теория двойственности
- •§1. Теория двойственности.
- •Тема 13. Транспортная задача.
- •§3. Транспортная задача.
- •3) Самостоятельное решение примеров:
- •3) Вопросы для самоконтроля:
- •Тема 14. Многоцелевая задача линейного программирования
- •§1. Многоцелевая задача линейного программирования.
- •Тема 15. Элементы теории игр
- •§2. Решение матричной игры.
- •Список рекомендуемой литературы
- •Приложение а. Варианты контрольных работ
- •Часть 1. Нелинейное программирование
- •Задание нп-1
- •Задание нп-2
- •Задание нп-3
- •Задание нп-4
- •Задание нп-5
- •Задание нп-6
- •Задание нп-7
- •Задание нп-8
- •Часть 2. Динамическое программирование Задание дп-1
- •Задание дп-2.
- •Задание дп-3
- •Часть 3. Линейное программирование
- •Задание лп-4
- •Задание лп-5
- •Задание лп-6
- •Часть 4. Некоторые применения линейного программирования Задание плп-1
- •Задание плп-2
- •Задание плп-3
- •Задание плп-4
- •Приложение б. Теоретические сведения
- •Глава 1. Модели динамического программирования
- •§1. Общая постановка задачи динамического программировании
- •§2. Принцип оптимальности и уравнения Беллмана
- •§3. Задача о распределении средств между предприятиями
- •§4. Общая схема применения метода дп. Задача об оптимальном распределении ресурсов между отраслями на п лет
- •§5. Задача о замене оборудования
- •§6. Задача прокладки трубопровода
- •7. Упражнения
- •Глава 2. О многоцелевой задачей линейного программирования и теории матричных игр
- •§1. Многоцелевая задача линейного программирования
- •1.1. Постановка многоцелевой задачи линейного программирования.
- •§2. Решение матричной игры
- •2.1. Геометрический метод решения матричной игры.
- •2.2. Решение матричной игры сведением к задаче линейного программирования
- •2.3. Игры с «природой».
- •Приложение в. Титульный лист контрольной работы
§3. Задача о распределении средств между предприятиями
Рассмотрим предложенную выше схему на конкретной задаче о распределении средств между предприятиями.
Пример 1. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S0=5 усл. ед. Размеры вложения в каждое предприятие кратны 1 усл. ед. Средства х, выделенные k-му предприятию (k=1, 2, 3, 4), приносят в конце грда прибыль fk(х). Функции fk(х) заданы таблично (табл. 3.1). Принято считать, что:
а) прибыль fk(х) не зависит от вложения средств в другие предприятия;
б) прибыль от каждого предприятия выражается в одних условных единицах;
в) суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.
Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль была наибольшей.
Таблица 3.1
x |
f1(х) |
f2(х) |
f3(х) |
f4(х) |
1 |
8 |
6 |
3 |
4 |
2 |
10 |
9 |
4 |
6 |
3 |
11 |
11 |
7 |
8 |
4 |
12 |
13 |
11 |
13 |
5 |
18 |
15 |
18 |
16 |
Решение. Обозначим через xk количество средств, выделенных k-му предприятию. (Нумерацию предприятий 1, 2, 3, 4 сохраняем в процессе решения неизменной.)
Суммарная прибыль равна
Z=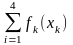 (3.1)
(3.1)
Переменные х удовлетворяют ограничениям:
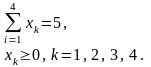 (3.2)
(3.2)
Требуется найти переменные х1, х2, х3, х4, удовлетворяющие системе ограничений (3.2) и обращающие в максимум функцию (3.1).
Особенности модели. Ограничения линейные, но переменные целочисленные, а функции fk(хk) заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.
Схема решения задачи методом ДП имеет следующий вид: процесс решения распределения средств S0=5 можно рассматривать как 4-шаговый, номер шага совпадет с номером предприятия; выбор переменных х1, х2, х3, х4 — управление соответственно на I, II, III, IV шагах. — конечное состояние процесса распределения — равно нулю, так как все средства должны быть вложены в производство, =0. Схема распределения показана на рис. 4.

Уравнения состояний (1.2) в данной задаче имеют вид:
Sk=Sk1xk, k=1, 2, 3, 4 (3.3)
где Sk — параметр состояния — количество средств, оставшихся после k-го шага, т.е. средства, которые остается распределить между оставшимися 4k предприятиями.
Введем в рассмотрение функцию (Sk1) — условную оптимальную прибыль, полученную от k-го, (k+1)-го, ..., 4-го предприятий, если между ними распределялись оптимальным образом средства Sk1 (0Sk15). Допустимые управления на k-м шаге удовлетворяют условию: 0xkSk1 (либо k-му предприятию ничего не выделяем, xk=0, либо не больше того, что имеем к k-му шагу, xkSk1).
Уравнения (2.1) и (2.4) имеют вид:
k=4,
S4=0
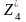 (S3)=
(S3)=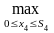 f4(x4),
(a)
f4(x4),
(a)
 (S2)=
(S2)=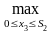 {f3(x3)+
(S3)}, (б)
{f3(x3)+
(S3)}, (б)
(S1)=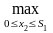 {f2(x2)+
(S2)}, (в)
{f2(x2)+
(S2)}, (в)
(5)=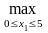 {f1(x1)+
(S1)}. (г)
{f1(x1)+
(S1)}. (г)
Последовательно решаем записанные уравнения, проводя условную оптимизацию (см. рис. 4) каждого шага.
IV ш а г. В табл. 1 f4(x) прибыли монотонно возрастают, поэтому все средства, оставшиеся к IV шагу, следует вложить в 4-е предприятие. При этом для возможных значений S3=0, 1, ..., 5 получим:
(S3)=f4(S3),
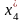 (S3)=S3.
(S3)=S3.
III шаг. Делаем все предположения относительно остатка средств S2 к III шагу (т.е. после выбора x1 и x2). S2 может принимать значения 0, 1,2, 3, 4, 5 (например, S2=0, если все средства отданы 1-му и 2-му предприятиям, S2=5, если 1-е и 2-е предприятия ничего не получили, и т.д.). В зависимости от этого выбираем 0x3S2, находим S3=S2x3 и сравниваем для разных x3 при фиксированном S2 значения суммы f3(x3)+ (S3). Для каждого S2 наибольшее из этих значений есть (S2) — условная оптимальная прибыль, полученная при оптимальном распределении средств S2 между 3-м и 4-м предприятиями. Оптимизация дана в табл. 2 при k=3. Для каждого значения (S2) и (S2) помещены в графах 5 и 6 соответственно.
II шаг. Условная оптимизация, согласно уравнению (в), проведена в табл. 2 при k=2. Для всех возможных значений S1 значения (S1) и (S1) находятся в столбцах 8 и 9 соответственно; первые слагаемые в столбце 7 — значения f2(x2), взяты из табл. 1, а вторые слагаемые взяты из столбца 5 табл. 2 при S2=S1x2.
I шаг. Условная оптимизация (уравнение (г)) проведена в табл. 2 при k=1 для S0=5 (На I шаге условной оптимизации достаточно заполнить раздел таблицы, соответствующий S0=5). Поясним решение подробно: если x1=0, то S1=5, прибыль, полученная от четырех предприятий при условии, что S1=5 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна f1(0)+ (5)=0+19=19 ( (5) взято из столбца 9 табл. 2 при S1=5). Если x1=1, то S2=4. Суммарная прибыль при условии, что S2=4 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна f1(1)+ (4)=8+16=24 (f1(1) взято из табл. , а (4) — из столбца 9 табл. 2.) Аналогично при x1=2, S2=3 и f1(1)+ (4)=10+13=23;
при x1=3, S2=2 и f1(3)+ (3)=11+10=21;
при x1=4, S2=1 и f1(4)+ (1)=12+16=28;
при x1=5, S2=0 и f1(5)+ (0)=18+0=18.
Сравнивая
подчеркнутые числа, получим
(5)=24
усл. ед.=Zmах
при
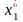 =
(5)=1.
=
(5)=1.
Используя
уравнения (3.3), получим
=51=4,
а по табл. 2 в столбце 9 находим
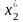 =
(4)=2.
Далее находим
=42=2,
а по табл. 2 в столбце 6 —
=
(4)=2.
Далее находим
=42=2,
а по табл. 2 в столбце 6 —
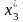 =
(2)=1.
Наконец,
=
(2)=1.
Наконец,
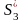 =21=1
и
=
(1)=1,
т.е.
=(1;
2; 1;
1).
=21=1
и
=
(1)=1,
т.е.
=(1;
2; 1;
1).
Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию — 2 усл. ед.; 3-му предприятию — 1 усл. ед.; 4-му предприятию — 1 усл.ед.
Замечание 1. Решение четырехмерной задачи 1 на определение условного экстремума сведено фактически к решению четырех одномерных задач: на каждом шаге определялась одна переменная х.
Замечание 2. На разобранной задаче 1 видно, что метод ДП безразличен к виду и способу задания функции: fk(х) были заданы таблично, поэтому и (S) и (S) принимали дискретные значения, представленные в Таблице 3.2.
Таблица 3.2
Sk1 |
xk |
Sk |
k=3 |
k=2 |
k=1 |
|||||||
f3(x3)+ + (S3) |
(S2) |
(S2) |
f2(x2)+ + (S2) |
(S1) |
(S1) |
f1(x1)+ + (S1) |
(S0) |
(S0) |
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0+4=4 |
|
|
0+4=4 |
|
|
0+6=6 |
8 |
1 |
|
1 |
0 |
3+0=3 |
4 |
0 |
6+0=6 |
6 |
1 |
8+0=8 |
|
|
||
2 |
0 |
2 |
0+6=6 |
|
|
0+7=7 |
|
|
0+10=10 |
|
|
|
1 |
1 |
3+4=7 |
7 |
1 |
6+4=10 |
10 |
1 |
8+6=14 |
14 |
1 |
||
2 |
0 |
4+0=4 |
|
|
9+0=9 |
|
|
10+0=10 |
|
|
||
3 |
0 |
3 |
0+8=8 |
|
|
0+9=9 |
|
|
0+13=13 |
|
|
|
1 |
2 |
3+6=9 |
9 |
1 |
6+7=9 |
13 |
1 |
8+10=18 |
18 |
1 |
||
2 |
1 |
4+4=8 |
|
|
9+4=13 |
|
2 |
10+6=16 |
|
|
||
3 |
0 |
7+0=7 |
|
|
11+0=11 |
|
|
11+0=11 |
|
|
||
4 |
0 |
4 |
0+13=13 |
|
|
0+13=13 |
|
|
0+16=16 |
|
|
|
1 |
3 |
3+8=11 |
|
|
6+9=15 |
|
|
8+13=21 |
|
|
||
2 |
2 |
4+6=10 |
13 |
0 |
9+7=16 |
16 |
2 |
10+10=20 |
21 |
1 |
||
3 |
1 |
7+4=11 |
|
|
11+4=15 |
|
|
11+6=17 |
|
|
||
4 |
0 |
11+0=11 |
|
|
13+0=13 |
|
|
12+0=12 |
|
|
||
5 |
0 |
5 |
0+16=16 |
|
|
0+18=18 |
|
|
0+19=19 |
|
|
|
1 |
4 |
3+13=16 |
|
|
6+13=19 |
|
|
8+16=24 |
|
|
||
2 |
3 |
4+8=12 |
18 |
5 |
9+9=18 |
19 |
1 |
10+13=23 |
24 |
1 |
||
3 |
2 |
7+6=13 |
|
|
11+7=18 |
|
|
11+10=21 |
|
|
||
4 |
1 |
11+4=15 |
|
|
13+4=17 |
|
|
12+6=18 |
|
|
||
5 |
0 |
18+0=18 |
|
|
15+0=15 |
|
|
18+0=18 |
|
|
||
Замечание 3. Альтернативой между ДП для подобной дискретной задачи является метод перебора. Метод ДП предпочтительнее, так как на этапе условной оптимизации отбрасываются заведомо негодные варианты.
Замечание 4. Достоинством метода является возможность анализа решения на чувствительность к изменению S0 и n. Проведенные расчеты можно использовать для изменившихся начального состояния S0 и числа шагов п. Например, пусть в задаче 1 произошло уменьшение начальных средств на 1 усл. ед. Для S0=4 достаточно в таблицу добавить расчеты при k=1 (это сделано в той же табл. 2). Получаем в этом случае Zmах=21 усл. ед. при распределении:
=1, =41=3 =1, или =2
=31=2, или =32=1 =1, или
=0 =21=1, или =10=1 =1.
В результате
найдены два оптимальных решения:
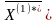 =(1;
1; 1; 1) и
=(1;
1; 1; 1) и
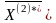 =(1;
2; 0;
1). Если
начальные средства увеличились, например,
на 1 усл. ед., S0=6,
а функции прибыли fk(х)
остались прежними, то в табл. 2 достаточно
добавить раздел для S0=6
при k=3,
2, 1; этот фрагмент расчетов помещен в
Таблице 3.3.
=(1;
2; 0;
1). Если
начальные средства увеличились, например,
на 1 усл. ед., S0=6,
а функции прибыли fk(х)
остались прежними, то в табл. 2 достаточно
добавить раздел для S0=6
при k=3,
2, 1; этот фрагмент расчетов помещен в
Таблице 3.3.
Таблица 3
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|||||||||||||||||
6 |
0 |
6 |
0+16=16 |
|
|
0+22=22 |
|
|
0+24=24 |
|
|
|||||||||||||||||
1 |
5 |
3+16=19 |
|
|
6+18=24 |
|
|
8+19=24 |
|
|
||||||||||||||||||
2 |
4 |
4+13=17 |
22 |
5 |
9+13=22 |
24 |
1 |
10+16=26 |
27 |
1 |
||||||||||||||||||
3 |
3 |
7+8=15 |
|
|
11+9=20 |
|
|
11+13=24 |
|
|
||||||||||||||||||
4 |
2 |
11+6=17 |
|
|
13+7=20 |
|
|
12+10=22 |
|
|
||||||||||||||||||
5 |
1 |
18+4=22 |
|
|
15+4=19 |
|
|
18+6=24 |
|
|
||||||||||||||||||
Получаем Zmах=27,
=1, =61=3 =1
=51=4 =0 =40=4 =4.
Оптимальное решение =(1; 1; 0; 4).
Если принято решение распределить средства S0=5 между 2-, 3- и 4-м предприятиями, то задача уже решена в табл. 2. В разделе k=2 таблицы находим Zmах= (5)=19 при условии, что =1, =0, =4.
Наконец, если
увеличилось количество предприятий
(число шагов), то схему можно дополнить,
присоединяя шаги с номерами k=0,
1,
... и т. д. Например, пусть средства S0=6
распределяются между пятью предприятиями.
Функция прибыли для пятого предприятия
задана формулой f(х)=3х+1,
если х≠0
и f(0)=0.
Присвоим 5-му предприятию номер k=0,
тогда x0
— средства, выделенные этому предприятию.
Обозначим через
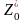 (6)
оптимальную прибыль, полученную от пяти
предприятий:
(6)
оптимальную прибыль, полученную от пяти
предприятий:
(6)=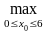 {f0(x0)+
(S1)},
{f0(x0)+
(S1)},
а S1=6x0.Условная оптимизация 0-го шага дана в табл. 4:
x0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
S1=6x0 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
f(0)=0 |
0 |
4 |
7 |
10 |
13 |
16 |
19 |
(S1) (взята из табл. 2 и 3 при k=1) |
27 |
24 |
21 |
18 |
14 |
8 |
0 |
f0(x0)+ (S1) |
27 |
28 |
28 |
28 |
27 |
24 |
19 |
Следовательно,
Zmах=28,
а оптимальных решений четыре:
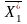 =(1;
1; 2; 1; 1),
=(1;
1; 2; 1; 1),
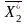 =(2;
1; 1; 1; 1),
=(2;
1; 1; 1; 1),
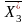 =(2;
1; 2; 0; 1),
=(2;
1; 2; 0; 1),
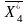 =(3;
1; 1; 0; 1).
=(3;
1; 1; 0; 1).
Замечание 5.
К недостаткам метода по-прежнему следует
отнести возникновение технических
трудностей при вычислениях в случае
увеличения размерности. Если каждое
управление
будет зависеть от r
переменных, а состояние

от p
параметров, то на каждом шаге возникает
rр-мерная
задача оптимизации. (В задаче 1
r=1,
р=1,
т.е. решалась одномерная задача). Даже
при реализации метода ДП на ЭВМ практически
можно решать задачи для небольших r,
р,
n.
от p
параметров, то на каждом шаге возникает
rр-мерная
задача оптимизации. (В задаче 1
r=1,
р=1,
т.е. решалась одномерная задача). Даже
при реализации метода ДП на ЭВМ практически
можно решать задачи для небольших r,
р,
n.
