1. Вывод основных уравнений четырёхполюсника.
Основные уравнения четырехполюсников:
U1=AU2+BI2
I2=CU2+DI2
A, B, С, D – коэффициенты четырехполюсника
A, В – безразмерные величины, B=Ом, D= 1/Ом
AВ-BC=1
A=D для симметричного четырехполюсника
2. Переход от изображения функции к её оригиналу. Формула разложения.
Переход от изображений к оригиналам осуществляется с помощью обратного преобразования Лапласа:
Найдем изображения некоторых простейших функций
1)
,
тогда:
2) , Тогда:
3) Тогда:
Переход от изображений к оригиналам осуществляется двумя способами:
1) По таблице изображений и оригиналов.
2) По формуле разложения (основной способ):
,
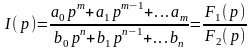где n>m;
- не имеет кратных корней, и корней,
кратных корням уравнения
.
В этом случае оригинал:
Число слагаемых в формуле разложения равно числу слагаемых в уравнении .
- производная
уравнения
.
В случае комплексных сопряженных корней формула разложения примет следующий вид:
3. Классификация электрических фильтров.
Электрический фильтр – это четырехполюсник, беспрепятственно пропускающий токи одних частот и не пропускающий или пропускающий с большими затуханием токи других частот.
Полоса пропускания (полоса прозрачности) – это диапазон частот, беспрепятственно пропускаемых фильтром. (a=0), а – коэффициент затухания.
Полоса затухания (полоса задерживания) – это диапазон частот, не пропускаемых фильтром или пропускаемая с большими затуханиями. (a>>0).
Частота среза (ωС) – это граничная частота между полосой пропускания и полосой задерживания.
Электрические фильтры, в зависимости от области пропускаемых частот делятся на следующие:
I) Низкочастотные (фильтры нижних частот) - ФНЧ
II) Высокочастотные (фильтры высоких частот) - ФВЧ
III) Полосовые фильтры - ПФ
IV) Заграждающие фильтры – ЗФ.
В зависимости от схемы соединения элементов фильтры делятся на:
1) Г – образные.
2) Т – образные.
3) П – образные.
4) Мостовые.
В зависимости от характеристики применяемых элементов:
1) Реактивные
2) Безиндуктивные (RC - фильтры)
3) Пьезоэлектрические
4) Цифровые.
Реактивные делятся на:
1) К – фильтры (или k - фильтры).
2) М – фильтры (или m - фильтры).
4. Формула разложения.
Переход от изображений к оригиналам осуществляется двумя способами:
1) По таблице изображений и оригиналов.
2) По формуле разложения (основной способ):
, где n>m; - не имеет кратных корней, и корней, кратных корням уравнения . В этом случае оригинал:
Число слагаемых в формуле разложения равно числу слагаемых в уравнении .
- производная уравнения .
В случае комплексных сопряженных корней формула разложения примет следующий вид:
5. Активные четырёхполюсники.
Четырёхпо́люсник — многополюсник, имеющий четыре точки подключения. Как правило, две точки являются входом, две другие — выходом.
С
хема
четырехполюсника
При анализе электрических цепей очень часто бывает удобным выделить фрагмент цепи, имеющий две пары зажимов. Поскольку электрические (электронные) цепи очень часто связаны с передачей энергии или обработкой и преобразованием информации, одну пару зажимов обычно называют «входными», а вторую — «выходными». На входные зажимы подаётся исходный сигнал, с выходных снимается преобразованный.
Такими четырёхполюсниками являются, например, трансформаторы, усилители, фильтры, стабилизаторы напряжения, телефонные линии, линии электропередачи и т. д.
Однако математическая теория четырёхполюсников не предполагает никаких преопределённых потоков энергии/информации в цепях, поэтому названия «входные» и «выходные» являются данью традиции и с этой оговоркой будут использоваться далее.
Состояния входных и выходных зажимов определяются четырьмя параметрами: напряжением и током во входной (U1, I1) и выходной (U2, I2) цепях. В этой системе параметров линейный четырёхполюсник описывается системой из двух линейных уравнений, причём два из четырёх параметров состояния являются исходными, а два остальные — определяемыми. Для нелинейных четырёхполюсников зависимость может носить более сложный характер. Например, выходные параметры через входные можно выразить системой
В дальнейшем будет использоваться запись системы уравнений в матричном виде, как наиболее удобная для восприятия.
Поскольку четырёхполюсник имеет четыре параметра состояния, очевидно, что имеется шесть систем уравнений, выражающих различные пары параметров через два остальных. Коэффициенты этих шести систем уравнений получили традиционное наименование A-, B-, G-, H-, Y- и Z-параметров.