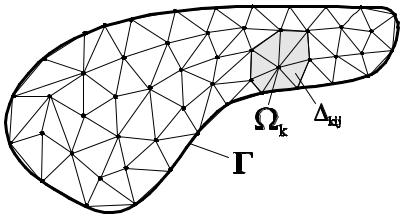
Двумерные финитные функции на треугольной сетке
Каждая пара треугольников имеет либо одну общую вершину, либо одну общую сторону, либо не пересекается.
Объединение |
U kij |
|
|
Узлы сетки обозначим |
|
P0 , P1,..Pk .., PN |
Pk xk , yk |
06/25/19 |
21 |
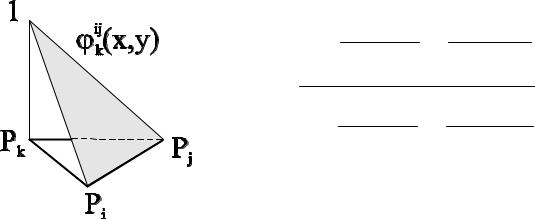
Финитная функция на треугольных конечных элементах
определим кусочно-линейную функцию |
kij (xy) |
, которая в |
|
|
||||||||
точке Pk равна единице, а в точках Pi, Pj равна нулю |
|
|
|
|||||||||
1 |
x x |
|
y y j |
|
|
|
|
|
||||
x |
|
i |
y |
y |
|
|
|
|
|
|
||
ij |
|
x |
|
|
1 ij (x x ) ij ( y y |
|
). |
|||||
|
j |
i |
|
i |
|
j |
k |
|||||
k |
x |
|
x |
|
yk y j |
k |
k |
k |
|
|||
1 |
|
|
|
|
|
|
|
|||||
k |
i |
y |
y |
|
|
|
|
|
|
|||
|
x |
j |
x |
|
j |
|
|
|
|
|
||
|
|
i |
|
i |
|
|
|
|
|
|
||
06/25/19 |
22 |
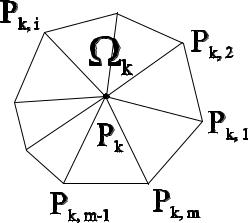
Базисные финитные функции
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
u ; uN (x, y) ak k (x, y) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
||
k k,k ,k |
2 |
|
k,k |
,k |
... k ,k |
m 1 |
,k |
m |
|||||||||||||
|
|
1 |
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|||||||
|
|
k ,k |
2 |
(xy), |
|
(xy) |
|
|
|
|
|
|
, |
|
|||||||
|
|
|
1 |
|
|
k,k1,k2 |
|
||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
........................................... |
|||||||||||||||||||
|
|
|
|
k |
|
|
|
,k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 1 |
m (xy), (xy) |
|
|
|
|
|
, |
||||||||||
k |
(xy) |
k |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k,km 1 ,km |
|||||||
|
|
|
|
k |
|
,k |
|
|
|
|
(xy) k ,k |
|
|
|
|
, |
|||||
|
|
k m |
|
1 (xy), |
|
,k |
|||||||||||||||
|
|
|
|
|
|
|
xy |
|
. |
|
|
|
m |
|
|
1 |
|||||
|
|
0, |
|
|
k |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
06/25/19 |
23 |
Финитные функции на тетраэдрах
Трехмерная область при выборе базиса вместо треугольной сетки покрывается сеткой из тетраэдров ∆kijl. Конечный элементk , связанный с узлом Pk(xk, yk, zk), состоит из тетраэдров, имеющих вершину Pk. Финитная функция k(x, y, z) строится из кусочно линейных функций тетраэдра
ijl 1 ijl (x x ) ijl ( y y |
k |
) ijl (z z |
k |
). |
|||||||||||||||||||
k |
k |
|
|
k |
k |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||
Коэффициенты находятся из решения системы |
|
|
|
|
|
|
|
|
|
||||||||||||||
1 ijl (x |
|
x |
) ijl ( y |
|
y |
k |
|
) ijl (z |
z |
k |
) 0; |
||||||||||||
k |
i |
k |
k |
i |
|
|
|
|
|
|
k |
i |
|
|
|
|
|
|
|||||
1 ijl (x |
j |
x |
) ijl ( y |
j |
y |
k |
) ijl (z |
j |
z |
k |
) 0; |
||||||||||||
k |
|
k |
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
||||||
1 ijl (x |
|
x |
) ijl ( y |
|
y |
k |
) ijl (z |
z |
k |
) 0. |
|||||||||||||
k |
l |
k |
k |
l |
|
|
|
|
|
|
k |
l |
|
|
|
|
|
|
|
||||
06/25/19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
Тетраэдр
06/25/19 |
25 |
Конец
06/25/19 |
26 |