
Презентации и конспект лекции Синицын / Презентации_ВЭиМОвТС / ВычЭксперим / Лекция3_ДифУравнения
.pdfТема 3.Постановка задач для дифференциальных уравнений
Определение дифференциальных уравнений
Постановка задач для обыкновенных ДУ
Постановка задач для ДУ в частных производных (ДУЧП)
Как получают дифференциальные уравнения
Подобие физических явлений, безразмерные переменные
05.01.2011 |
1 |
Определение дифференциальных уравнений
|
u |
|
u u u 2 u 2 u 2 u 2 u |
|
|||||||||||||||||
x , y , z , t , u ( x , y , z , t ), |
|
, |
|
, |
|
, |
|
, |
|
|
, |
|
|
, |
|
|
, |
|
|
|
f ( x , y , z , t ) |
x |
y |
z |
t |
x |
2 |
y |
2 |
z |
2 |
t |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
•Порядок ДУ =максимальный порядок входящих в это уравнение производных
•Порядок системы ДУ = сумме порядков входящих ДУ
•Эквивалентность системы и одного ДУ
•Два класса: обыкновенные ДУ (ОДУ), которые описывают процессы, зависящие от одной независимой переменной , и ДУ в частных производных (ДУЧП)
05.01.2011 |
2 |

Обыкновенные ДУ
•Система ОДУ первого порядка
d u |
1 |
|
|
f1 ( x , u1 , u 2 , ..., u m ); |
|
|
|
||
• |
|
|
или коротко |
||||||
d x |
|||||||||
|
|
|
|
|
|
||||
.......................................... |
|
d u |
|
||||||
d u |
|
|
|
|
|
f ( x , u ). |
|||
|
|
|
|
|
|
||||
|
|
m |
|
f m ( x , u1 , u 2 , ..., u m ). |
|
d x |
|||
|
|
|
|
||||||
|
d x |
|
|
|
|||||
|
|
|
|
|
|||||
• Система ОДУ второго порядка
|
|
( g 1 |
u |
1 |
) q1 |
u |
1 |
|
p1u1 f ( x , u 2 , ..., u m , |
u |
2 |
, ..., |
u |
m |
); |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
|
x |
|
x |
|
|
x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
..................................................................................... |
|
|
||||||||||||||||||||
|
|
|
|
u m |
|
|
u m |
|
|
|
|
u1 |
|
|
|
u m 1 |
|
|||||
|
( g m |
|
) q m |
p m u m f ( x , u1 , ..., u m 1 , |
, ..., |
). |
||||||||||||||||
x |
|
x |
|
x |
x |
|
x |
|||||||||||||||
|
|
|
|
|||||||||||||||||||
05.01.2011 |
u u1 ( x ), ..., u m ( x ) |
a x b |
3 |

Постановка задач для обыкновенных ДУ
Известно, что система ОДУ имеет бесконечное семейство
решений |
u u ( x , C ) |
|
|
|
|
C (c1 , ..., cm ) |
набор произвольных параметров |
|
их количество равно порядку системы m.
Это семейство решений описывает многообразие реализаций физического процесса, математической моделью которого являются системы ОДУ.
Для выделения одной искомой реализации среди этого многообразия необходимо наложить дополнительные условия конкретизирующие искомое решение
Количество этих условий равно порядку m системы ОДУ.
В зависимости от способа постановки дополнительных условий можно выделить два основных типа задач для ОДУ
Задача Коши и Краевая задача
05.01.2011 |
4 |

Задача Коши
•Все условия заданы в начале отрезка интегрирования [a,b] (при x=a).
•Эта задача чаще всего ставится для системы
•
d u f ( x , u ). d x
•в виде
u1 ( a ) u10 ; ... u m ( a ) u m0
• Или коротко |
u ( a ) u |
0 |
|
||
|
|
05.01.2011 |
5 |
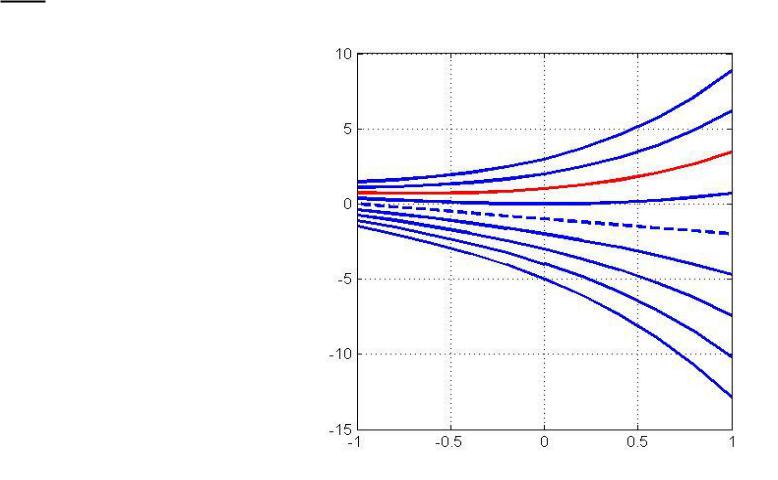
Пример точного решения
d u u x
d x
u
u ( 0 ) 1
u C e x x 1
C 2
x
C=4
C=2
C=-4
05.01.2011 |
6 |
Краевая задача
Условия заданы на обоих концах отрезка [a,b].
Эта задача обычно ставится для ДУ второго порядка
|
( g |
u |
) q |
u |
p u f ( x , u ) |
|
|
|
|||
x |
x |
x |
|||
В общем случае |
|
||||
a |
d u ( a ) |
a u ( a ) a ; |
п р и x a |
||
|
|
||||
|
|
d x |
|
||
b |
d u ( b ) |
b u ( b ) b ; |
п р и x b |
||
|
|||||
|
|
d x |
|
||
05.01.2011 |
7 |
Пример точного решения ДУ
•Рассмотрим ДУ вида
•Граничные условия
•Проинтегрируем
•Левая часть
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
f ( x ); |
|
0 x |
|
1 . |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
g ( x ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
q |
0 u |
|
0 |
u |
|
|
|
|
0 |
; q |
1 u |
|
1 |
u |
|
|
1 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
g |
|
|
|
|
d x |
f ( x ) d x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 |
|
x |
|
|
|
|
x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
|
|
|
|
|
|
|
u |
|
|
|
u |
|
|
x |
|
|
|
|
u ( x ) |
|
|
u |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
g |
|
|
|
|
d x g |
|
|
|
|
g ( x ) |
|
|
|
|
|
|
g ( 0 ) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
0 |
x |
|
|
|
|
x |
|
|
|
|
x |
|
0 |
|
|
|
|
x |
|
|
|
|
x |
|
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
• Обозначим |
x |
|
f ( x ) d x p ( x ) |
||
|
||
|
0 |
05.01.2011 |
8 |

Пример точного решения ДУ (продолжение1)
•Обозначим c1 g ( 0 ) u
x 0
•Получаем уже диф.ур. первого порядка
• |
|
g ( x ) |
u ( x ) |
p ( x ) |
c1 |
или |
|
u ( x ) |
|
|
|
p ( x ) c1 |
|
|
|
||||||||||||
|
|
x |
|
|
|
x |
|
|
g ( x ) |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
• |
Проинтегрируем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
u ( x ) |
d x u ( x ) u ( 0 ) x |
p ( x ) c1 |
d x x |
|
p ( x ) |
d x c |
|
x |
1 |
d x |
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||
|
|
|
x |
|
|
|
|
g ( x ) |
|
|
|
|
|
g ( x ) |
|
|
|
g ( x ) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
• |
Обозначим с2=u(0) |
|
|
|
|
x |
|
p ( x ) |
|
|
|
|
x |
|
1 |
|
|
|
|
||||||||
• |
Получаем решение ДУ |
u ( x ) c2 |
|
|
|
|
|
d x c1 |
|
|
|
|
d x |
|
|||||||||||||
|
|
g ( x ) |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g ( x ) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
05.01.2011 |
9 |
Пример точного решения ДУ (продолжение2)
Нахождение констант с1,с2, из граничных условий
|
|
|
|
0 |
u |
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
c1 |
|
|
|||||
• |
Из |
q |
|
|
|
u |
|
|
|
|
|
|
|
; используя |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x 0 |
|
|
|
|
|
|
x |
|
|
0 |
|
g ( 0 ) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
q 0 |
( c |
|
|
|
) 0 c |
|
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
• |
Получим |
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g ( 0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
• |
Из |
q 1 |
u |
1u |
|
|
|
|
|
1 ; |
|
|
используя |
|
u (1) |
|
|
p (1) |
c1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
g (1) |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
p (1) |
|
|
|
|
|
|
1 |
|
|
|
p ( x ) |
|
|
1 |
|
|
|
|
|
|||||||||||||
• |
Получим |
|
|
q1 ( |
|
|
c1 |
|
|
) 1 ( c2 |
|
|
d x c1 |
|
d x ) |
1 ; |
||||||||||||||||||||||||
|
|
g (1) |
|
g (1) |
g ( x ) |
g ( x ) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
•Имеем систему двух ур-й относительно с1 и с2
05.01.2011 |
10 |
