2.6. Наращение денежных средств с использованием простой учетной ставки

Операцию наращения по простой учетной ставке применяют в краткосрочных ФО с векселями продолжительностью до одного года, когда возникает необходимость определения номинальной стоимости FV, которую следует проставить в векселе, если известна текущая величина долга PV [2]. Формула наращения простыми процентами с использованием учетной ставки d имеет вид:

.

(2.17)

Рис. 2.4. Сравнение темпов роста

денежных средств по простым

ставкам: FV_ds – сумма, наращенная

по простой учетной ставке;

FV_is – сумма, наращенная

по простой процентной ставке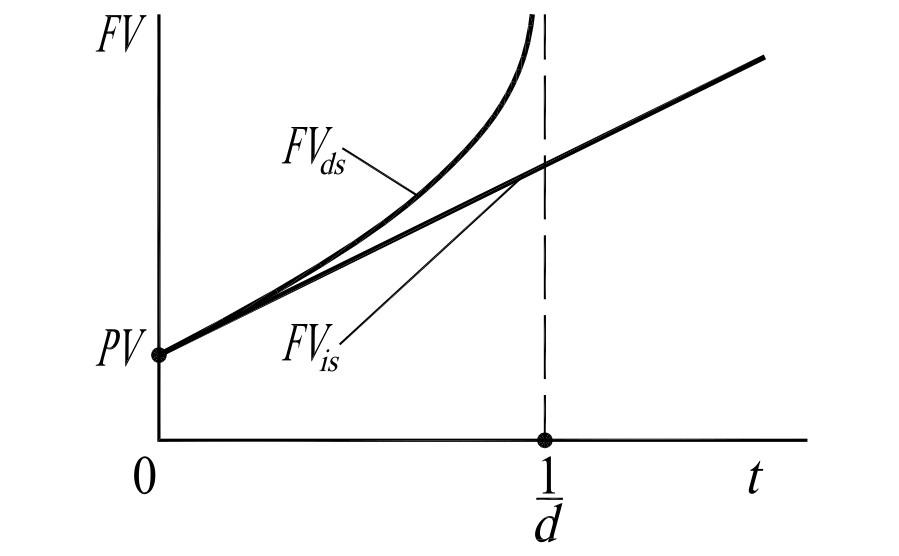

В данной формуле множитель называют множителем наращения. Этот множитель соответствует индексу роста B. Он всегда больше единицы, поэтому наращенная сумма FV всегда больше современной стоимости PV. Для этого знаменатель должен быть меньше единицы (но больше нуля), следовательно, должно выполняться неравенство , тогда . Таким образом, функция наращения по простой учетной ставке (рис. 2.4) асимптотически приближается к вертикальной линии . В предельном случае при расчет не имеет смысла, т. к. функция обращается в бесконечность. Темпы роста денежных средств при наращении по про­с­той учетной ставке выше, чем по простой процентной ставке.

Сумму процентов, начисленную за период времени t, с учетом формул (1.1) и (2.17) определяют по формуле

.

(2.18)

Формула (2.18) показывают, что зависимость суммы начисленных процентов I от продолжительности ФО t нелинейная (см. рис. 2.3, 2.4). Формула также показывает, что, в отличие от наращения по простой процентной ставке i, проценты, начисленные по простой учетной ставке d за очередной период начисления, выше, чем за предшествующий период, равный ему по продолжительности [2].

Если возникает необходимость определения суммы начисленных процентов за несколько промежуточных периодов или за отдельные промежуточные периоды, можно использовать следующие формулы:

• за первый период или , где  – наращенная сумма за первый период, определяемая по формуле (2.17);

• за два периода ;

за второй период

или . Сравнивая формулы для и , нетрудно заметить, что знаменатель в формуле меньше знаменателя в формуле в раз, т. к. величина в каждой скобке меньше единицы. Следовательно, в раз;

• …;

• за весь период ФО (за все t периодов) ;

за последний период

или .

2.7. Наращение денежных средств с использованием сложной учетной ставки

Операцию наращения по сложной учетной ставке применяют в средне- и долгосрочных ФО продолжительностью более одного года. Наращенную сумму F при этом определяют по формуле

.

(2.19)

В данной формуле множитель наращения равен . Этот множитель соответствует индексу роста B. Он всегда больше единицы, поэтому наращенная сумма FV всегда больше современной стоимости PV. Сумму процентов, начисленную за период времени t, с учетом формул (1.1) и (2.19) определяют по формуле

.

(2.20)

Формула (2.20) показывают, что зависимость суммы начисленных процентов I от продолжительности ФО t нелинейная (см. рис. 2.3). Формула также показывает, что, в отличие от наращения по простой процентной ставке i, проценты, начисленные по сложной учетной ставке d за очередной период начисления, выше, чем за предшествующий период, равный ему по продолжительности.

Если возникает необходимость определения суммы начисленных процентов за несколько промежуточных периодов или за отдельные промежуточные периоды, можно использовать следующие формулы:

• за первый период или , где  – наращенная сумма за первый период, определяемая по формуле (2.19);

• за два периода ;

за второй период или ;

• …;

• за весь период ФО (за все t периодов) ;

за последний период или .

Если в ФО предусмотрено начисление процентов k раз в году, то задают продолжительность ФО n в годах и номинальную годовую учетную ставку d. Тогда формула (2.19) примет вид:

.

(2.21)

Тогда можно считать формулу (2.19) частным случаем данной формулы при и . При использовании формулы (2.21) следует формально принимать в случаях, когда продолжительность ФО меньше или равна одному году.