6.3. Консолидация платежей

Под консолидацией платежей понимают такое изменение условий ФО, при котором несколько платежей, имеющих будущие стоимости и сроки погашения , заменяют одним новым платежом, имеющим будущую стоимость и срок погашения . Если при этом установлен срок погашения , то задача сводится к определению будущей стоимости заменяющего платежа. В зависимости от используемой ставки можно выразить величину из соответствующего уравнения эквивалентности (6.7)–(6.10):

• при использовании простой процентной ставки

;

(6.25)

• при использовании сложной процентной ставки [2]

;

(6.26)

• при использовании простой учетной ставки

;

(6.27)

• при использовании сложной учетной ставки [2]

.

(6.28)

Если сроки погашения платежей и заданы в днях , то с учетом формулы (1.6) можно преобразовать, например, формулу (6.25):

.

(6.29)

Если при консолидации платежей участники ФО пришли к соглашению о будущей стоимости заменяющего платежа, то задача сводится к определению срока погашения заменяющего платежа. В соответствии с уравнением эквивалентности (6.6) сумма не может назначаться меньше суммы приведенных стоимостей , которую можно определить из уравнений (6.7)–(6.10). Если это условие не будет выполнено, то получится отрицательное значение срока погашения . В зависимости от используемой ставки можно выразить величину из соответствующего уравнения эквивалентности (6.7)–(6.10), причём для сложных ставок обе части уравнения эквивалентности после элементарных алгебраических преобразований логарифмируют с использованием натуральных или десятичных логарифмов [2]:

• при использовании простой процентной ставки

,

(6.30)

где ;

• при использовании сложной процентной ставки

,

(6.31)

где ;

• при использовании простой учетной ставки

,

(6.32)

где ;

• при использовании сложной учетной ставки

,

(6.33)

где .

Если сроки погашения платежей и заданы в днях , то с учетом формулы (1.6) можно преобразовать, например, формулу (6.30):

.

(6.34)

Пример 6.3. Два платежа на суммы 10 000 рублей и 20 000 рублей со сроками уплаты 3 месяца и 4 месяца заменили одним платежом со сроком уплаты 5 месяцев. Ставка наращения – 20% годовых. Опре­делить сумму заменяющего платежа для четырех основных ставок ( , , , ).

Решение.

руб.;

мес.;

руб.;

мес.;

мес.;

.

Продолжительность данной ФО выражается в месяцах, поэтому в расчетных формулах выполняем подстановку (1.7): .

Для четырех основных ставок определим сумму заменяющего платежа по формулам:

– для простой процентной ставки (6.25)

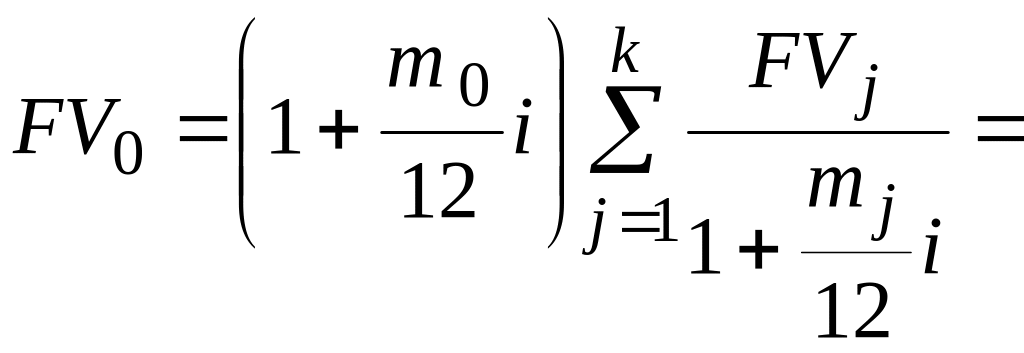
(руб.);

– для сложной процентной ставки (6.26)

(руб.);

– для простой учетной ставки (6.27)

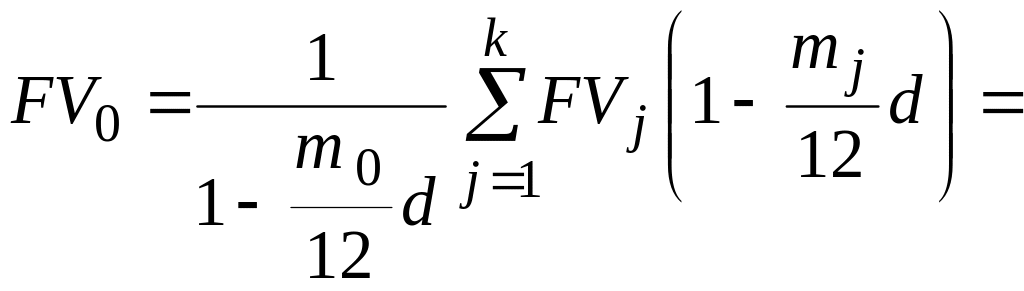
(руб.);

– для сложной учетной ставки (6.28)

(руб.).

Продолжительность данной ФО не превышает 1 года, поэтому наибольшая сумма заменяющего платежа получилась при использовании сложной учетной ставки.

Пример 6.4. Два платежа на суммы 10 000 рублей и 20 000 рублей со сроками уплаты 3 месяца и 4 месяца заменили одним платежом. Ставка наращения – 20% годовых. Опре­делить минимально возможную сумму заменяющего платежа для четырех основных ставок ( , , , ). В качестве примера увели­чить наибольшую из полученных сумм на 15% и определить срок уплаты полученного пла­тежа для четырех основных ставок.

Решение.

руб.;

мес.;

руб.;

мес.;

.

Продолжительность данной ФО выражается в месяцах, поэтому в расчетных формулах выполняем подстановку (1.7): .

Для четырех основных ставок определим минимально возможную сумму заменяющего платежа по формулам:

– для простой процентной ставки (6.30) ;

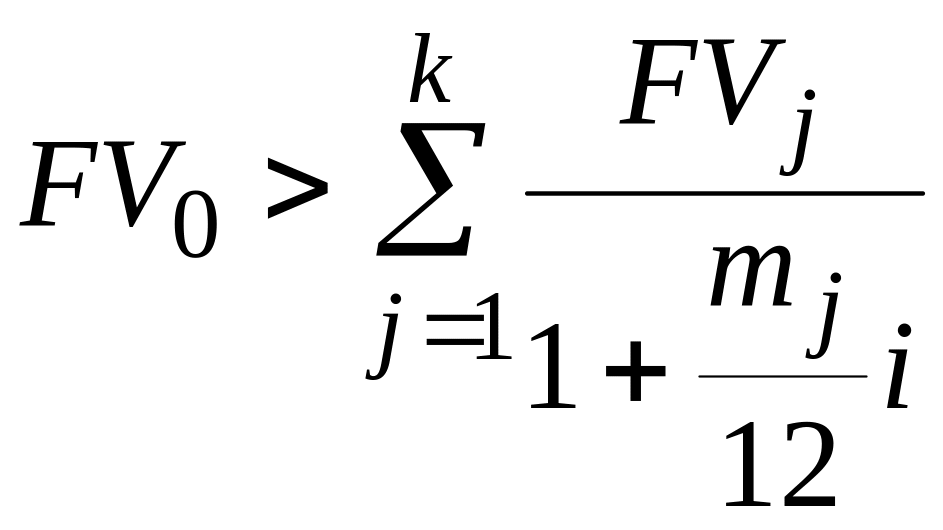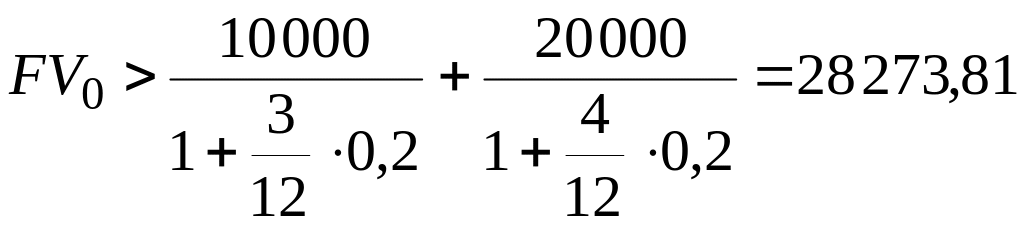; руб.;

– для сложной процентной ставки (6.31) ;

; руб.;

– для простой учетной ставки (6.32) ;

; руб.;

– для сложной учетной ставки (6.33) ;

; руб.

Наибольшая из полученных сумм составляет 28 375,15 руб. Увеличиваем ее на 15% и получаем условную сумму заменяющего платежа:

(руб.).

Для четырех основных ставок определим срок уплаты заменяющего платежа руб. по формулам:

– для простой процентной ставки (6.30)

(мес.);

– для сложной процентной ставки (6.31)

(мес.);

– для простой учетной ставки (6.32)

(мес.);

– для сложной учетной ставки (6.33)

(мес.).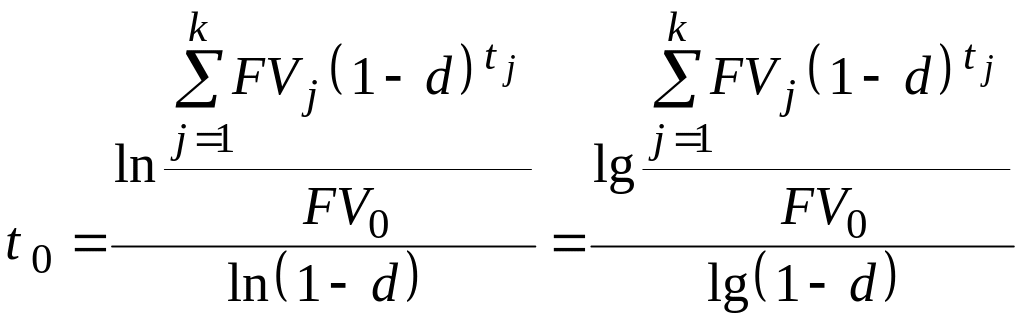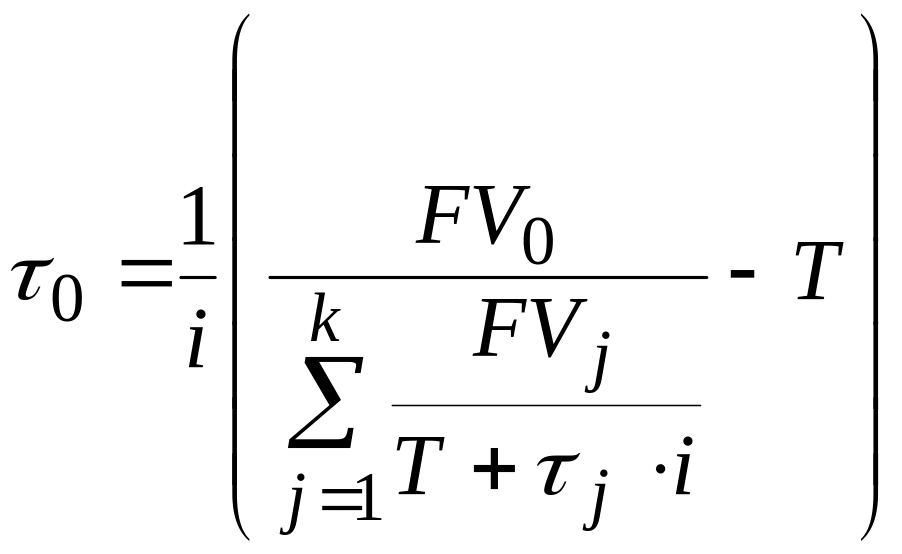