2.5 Усечённое нормальное распределение

Если в (2.1) положить x=t, то функция плотности распределения вероятностей классического нормального распределения запишется как

. (2.29)

Условие нормирования этой функции: 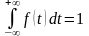, (2.30)

т.е. площадь под кривой распределения в пределах 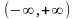равна 1.

Очевидным недостатком модели (2.29) является тот факт, что нормальная функция распределения не является односторонней, то есть отличной от нуля при t < 0 (см. Рис.2.3). Поскольку случайная величина – наработка до отказа Т – теоретически изменяется в пределах от нуля до бесконечности, необходимо часть кривой f(t), определяемой формулой (2.29), для t<0 отсечь (т.е. устранить из рассмотрения). В этом случае имеет место усечённое нормальное распределение (см. Рис.2.4). Чтобы сохранить условие нормирования, а именно – площадь под кривой усечённого нормального распределения должна быть равна единице, вводится коэффициент усечения С₀.

0,3

0,3

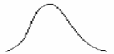f(t) f(t)

0,1

0,1

- 3 -2 -1 0 1 2 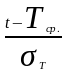0 Т t

Рис.2.3 Плотность вероятности Рис.2.4 Плотность вероятности

нормального распределения . усечённого нормального

распределения.

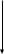
Для нахождения коэффициента усечения С₀ запишем условие нормирования, которое для классического нормального распределения определялось формулой (2.30): 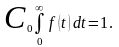(2.31)

Откуда коэффициент усечения 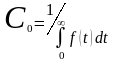. (2.32)

С учётом (2.29) 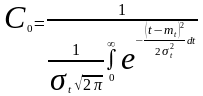. (2.33)

Введём новую переменную:

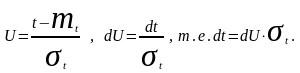
Пределы изменения новой переменной:

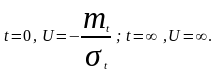
Подставив в (2.33) новую переменную с учётом новых пределов интегрирования, получим: (2.34)

Знаменатель формулы (2.34) есть интеграл Лапласа. Поясним далее понятия этого интеграла и нормированной функции Лапласа. Если принять условия нормирования m_t=0 и _t=1, то с учётом (2.29) нормированная функция плотности вероятности записывается как

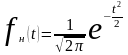. (2.35)

Эта функция симметрична относительно оси ординат, т.к. m_t=0; «высота» функции равна 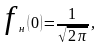а при ордината функции равна 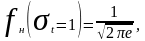т.е. она в 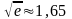раз меньше «высоты».

Интеграл Лапласа записывается в виде 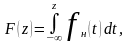(2.36)

где f(t) – нормированная функция классического нормального распределения (2.35). Выражение (2.36) определяет площадь под кривой распределения в пределах от 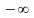до z. При z=0 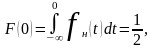(2.37)

т.к. кривая f(t) симметрична относительно оси ординат с учётом условия нормирования. При 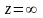с учётом (2.29) .

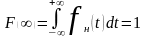Значения интеграла Лапласа приводятся в справочных таблицах.

Нормированная функция Лапласа имеет вид: (2.38)

где 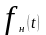определяется выражением (2.35). Формула (2.38) определяет площадь под кривой в пределах от 0 до z. При имеем:

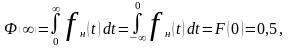(2.39)

то есть

Cледовательно, при 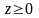F(z) = 0,5 +Ф(z). (2.40)

1.Нормированная функция Лапласа Ф(z) изменяется в пределах от нуля до 0,5 при изменении z от нуля до бесконечности.

2. Нормированная функция Лапласа Ф(z) является нечётной:

Ф(-z) = - Ф(z). (2.41)

Значения Ф(z) приводятся в справочных таблицах .

C учётом (2.40) можно записать 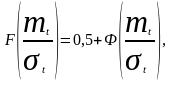следовательно, коэффициент усечения равен:

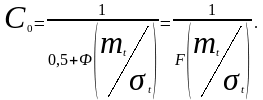(2.42)

Значения С₀ для различных соотношений 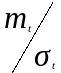приведены в табл.2.1

Таблица 2.1

	0,5	1,0	1,5	2,0	3,0	4,0	5,0
С0	1,446	1,188	1,071	1,023	1.001	,0	,0

Из таблицы видно, что С₀ – положительное число, большее единицы или близкое к ней. При этом C₀ > 1, если отношение находится в пределах (0,5 . . 1,5), т.е. функция плотности распределения «низкая» и «широкая» – в этом случае значение С₀, превышающее единицу, показывает, какая часть площади кривой отсекается усечённым распределением. К примеру, для = 1,0 отсекается 18,8% площади кривой.

С учётом (2.42) усечённое нормальное распределение записывается в виде: . (2.43)