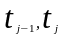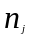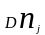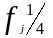5. Построение гистограмм

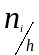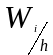Гистограммой частот (относительных частот) называют ступенчатую фигуру, состоящую из прямоугольников, основанием которых служат частичные интервалы (разряды) длиною h, а высоты равны отношению (оценка среднего значения плотности вероятностей частоты на интервале) или отношению (оценка среднего значения плотности вероятностей относительной частоты на интервале).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы (разряды) – их число обычно выбирают порядка 10-20, длины разрядов могут быть как одинаковыми, так и различными.

Над каждым из разрядов проводят отрезки, параллельные оси абсцисс на расстоянии , т.е. на каждом из разрядов как на основании строится прямоугольник, площадь которого равна частоте данного разряда. Площадь i-того частичного прямоугольника равна - сумме частот вариант i-того интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки.

На Рис.5.1 показана гистограмма частот распределения объёма n=100, приведенного в Таблице5.1

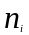
Частичный интервал длиною h=5	Сумма частот вариант Частичного интервала	Плотность частоты
5 – 10	4	0,8
10 – 15	6	1,2
15 – 20	16	3,2
20 – 25	36	7,2
25 – 30	24	4,8
30 – 35	10	2,0
35 - 40	4	0,8

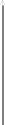
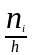
7

6

5

4

3

2

1

0 5 10 15 20 25 30 35 40 х

Рис.5.1 Гистограмма частот.

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы (разряды), а над ними проводят отрезки, параллельные оси абсцисс на расстоянии 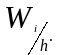Площадь i-того частичного прямоугольника равна 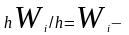относительной частоте вариант, попавших в i-тый интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

При обработке статистического материала по надёжности по данным выборки строят гистограммы показателей безотказности, для чего используют следующие формулы, предварительно разбив на интервалы t весь диапазон наработок:

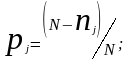
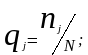
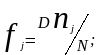
(5.1)

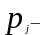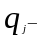где вероятность безотказной работы; вероятность отказа;

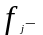плотность распределения относительных частот; 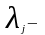интенсивность отказов;

j – номер интервала, j=1,2,…,k. k-число интервалов;

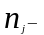число отказов к началу j-того интервала;

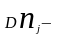число отказов в j-том интервале;

N – число изделий, поставленных на испытание (объём выборки).

Пример. Имеется выборка объёмом N=48 в виде вариационного ряда, представляющего собой наработки до отказа 2,3,4,5,5,6,7,7,8,8,9,9,9,10,

10,11,11.11,12,12,12,13,13,13.14,14,14.14,15,15,15,16,16,16,17,17.18,18,

18,19,19,20,20,21,21,22,23,24. Требуется: определить n(t) – число отказов за наработку t; 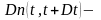число отказов в интервал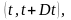е где 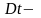длина интервала наработки; построить гистограммы плотности распределения относительных частот 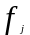, а также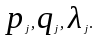

Решение: 1.Задаёмся значением наработки и находим число отказов за наработку t:

а) t=10 час. n(10) = 15; б) t=12 час. n(12) = 21; в) t=14 час. n(14) = 28.

2.Находим число отказов в интервале

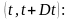
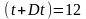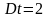а) t=10 час. час. час.

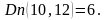
б) t=12 час. час. час.

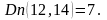
3.По данным выборки заполним Табл.5.2 для

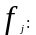
Таблица 5.2

Номер интервала
1	0….2	0	1	0,0104
2	2….4	1	2	0,0208
3	4….6	3	3	0,0312
4	6….8	6	4	0,0416
5	8….10	10	5	0,0520
6	10….12	15	6	0,0624
7	12….14	21	7	0,0728
8	14….16	28	6	0,0624
9	16….18	34	5	0,0520
10	18….20	39	4	0,0416
11 12	20….22 22….24	43 46	3 2	0,0312 0,0208

4.Гистограмма приведена на Рис5.2.

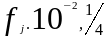
8

7

6

5

4

3

2

1

0 2 4 6 8 10 12 14 16 18 20 22 24 t

Рис.5.2. Гистограмма плотности распределения относительных частот.

Аналогично строят гистограммы используя формулы (5.1) и данные таблицы 5.2.