Элементарные путь и перемещение
Элементарное перемещение за бесконечно малый промежуток времени dt обозначается dr .
Элементарный путь обозначается как dS.
Для конечных промежутков времени в общем случае
|
S12 |
r |
Для элементарных перемещений можно записать dr dS.
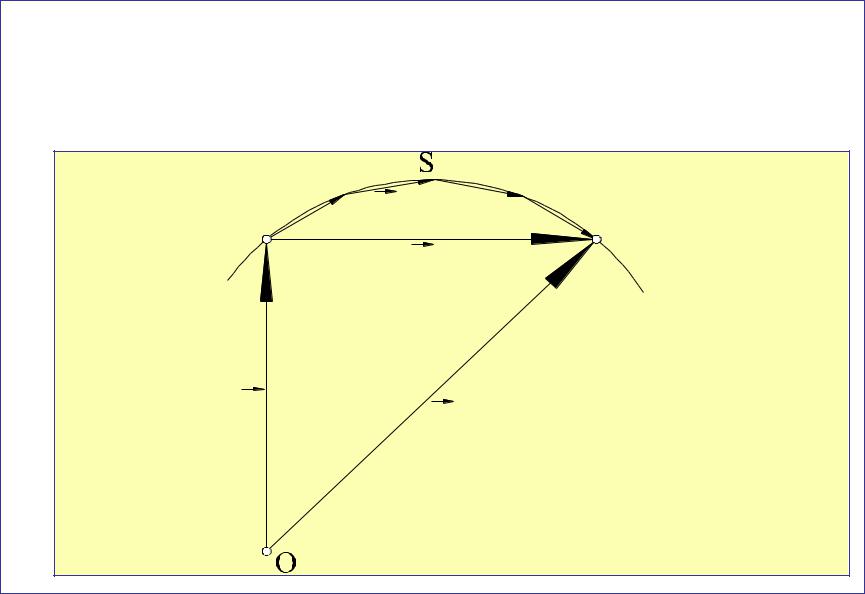
Перемещение по траектории из точки 1 в точку 2 можно представить как сумму бесконечно большого числа элементарных перемещений dr .
|
|
12 |
1 |
dr |
2 |
|
||
|
|
r |
r1 r2
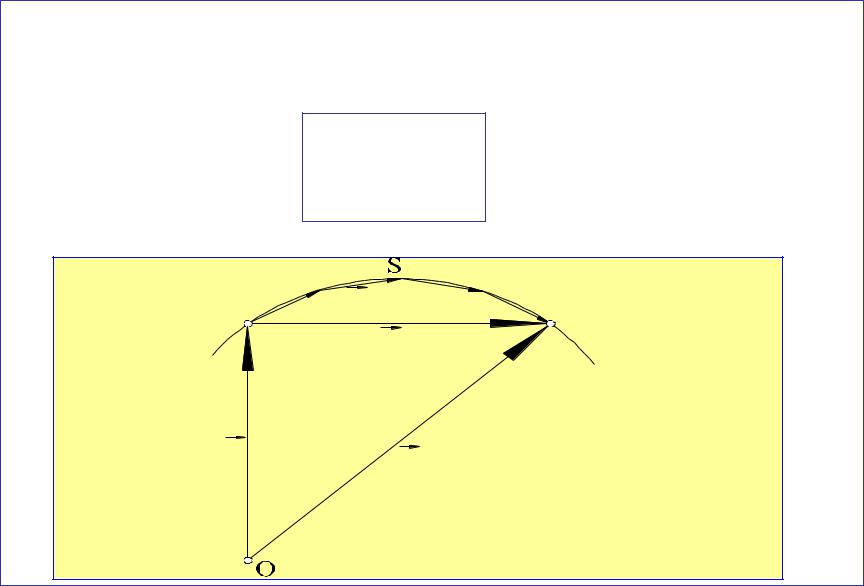
Вектор перемещения получим, просуммировав |
|||
элементарные перемещения: |
|||
|
|
r2 |
|
|
r dr |
||
|
|
|
|
|
|
r1 |
|
|
|
12 |
|
1 |
dr |
|
2 |
|
r |
||
|
|
|
|
r1 |
|
r2 |
|
|
|
|
|
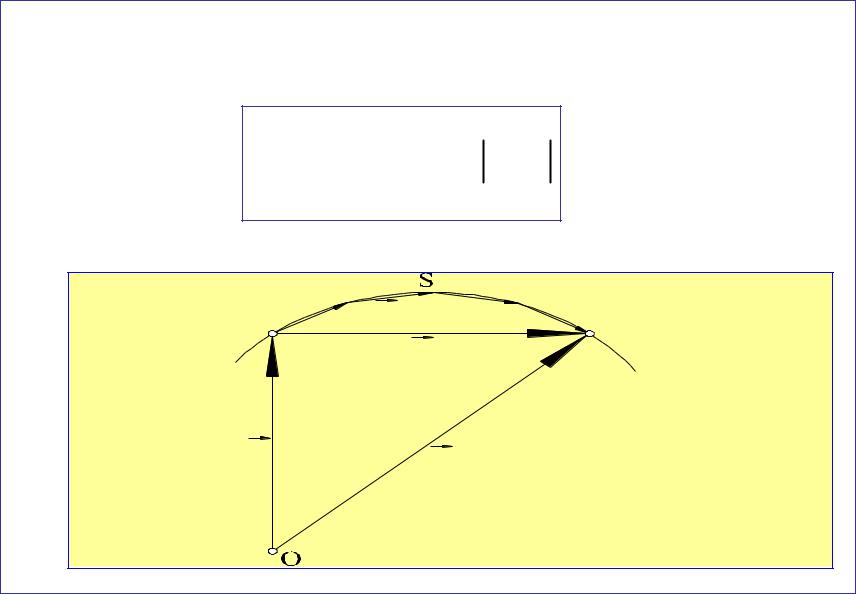
При интегрировании (суммировании) модулей |
|||
элементарных перемещений получим путь. |
|||
|
|
r2 |
|
|
|
|
|
S12 dS dr |
|||
|
S12 |
r1 |
|
|
|
12 |
|
1 |
dr |
|
2 |
|
r |
||
|
|
|
|
r1 |
|
r2 |
|
|
|
|
|
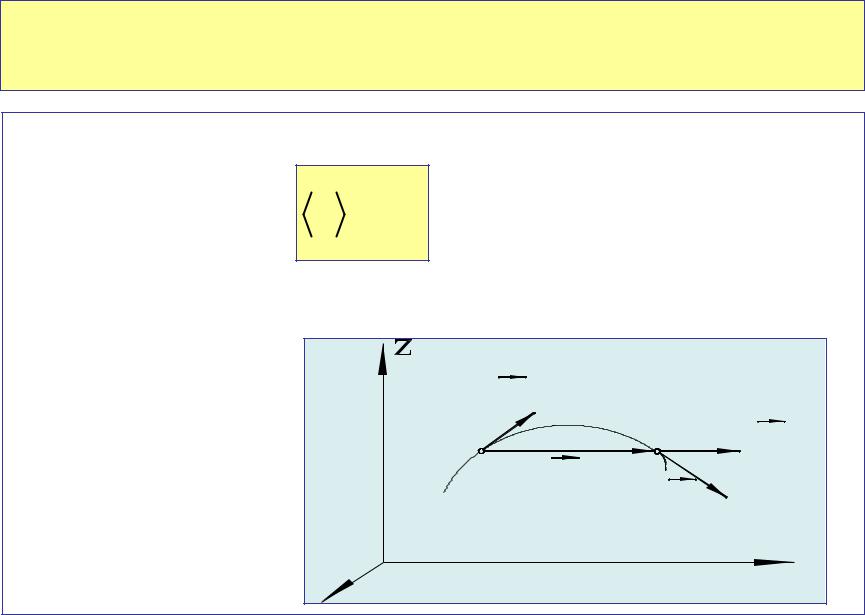
Скорость
Скорость характеризует быстроту изменения пространственного положения материальной точки.
Скорость равна перемещению, совершенному точкой за единицу времени.
|
|
V 1 |
<V > |
|
1 |
2 |
|
|
|
r |
2 |
|
|
|
|
x |
0 |
|
y |
|
Средняя скорость |
|
|
|
Вектор средней скорости за промежуток времени t |
||||
равен |
|
r |
|
|
|
v |
t |
|
|
Вектор средней скорости < v > направлен вдоль |
||||
вектора r . |
|
|
|
|
|
|
V 1 |
|
<V > |
|
|
1 |
2 |
|
|
|
r |
|
2 |
|
|
|
|
|
|
x |
0 |
|
y |
Среднее значение модуля скорости равно
v 
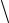S
t
Среднее значение модуля скорости - скалярная величина.
|
|
V 1 |
S |
<V > |
|
|
|
||
|
1 |
|
2 |
|
|
|
|
r |
2 |
|
|
|
|
|
x |
0 |
|
|
y |
При движении средняя скорость изменяет направление и величину.
Мгновенная скорость
Мгновенная скорость равна пределу вектора средней скорости при неограниченном убывании промежутка времени до нуля ( t 0).
|
|
|
|
|
|
|
lim |
Δr |
|
dr |
|||
v |
Δt |
dt |
||||
|
Δt 0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
v |
|
dr |
|
|
|
|
dt |
|
|
|
|
||
Мгновенная скорость равна первой производной от радиуса-вектора по времени.
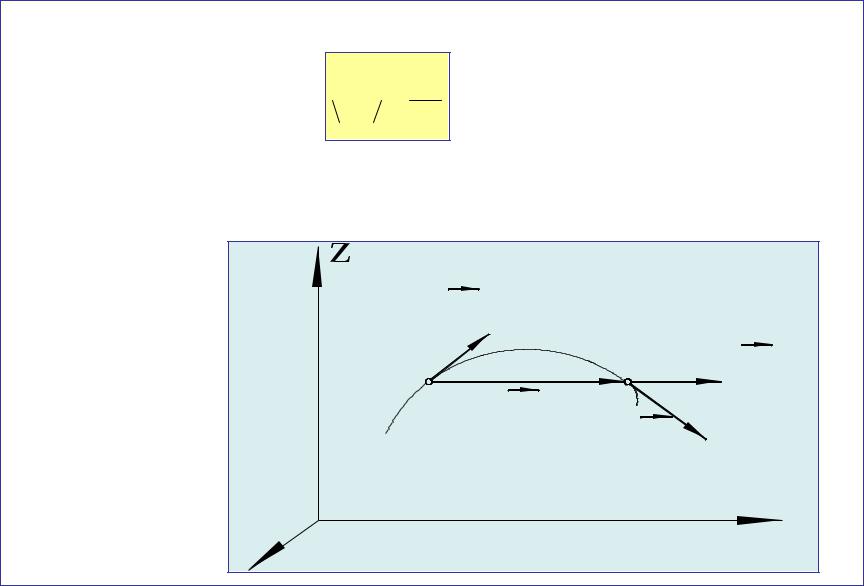
Вектор мгновенной скорости v направлен по вектору dr , т. е. по касательной к траектории.
Модуль мгновенной скорости равен:
v dr dS dt dt
Скорость измеряется в м/с.
|
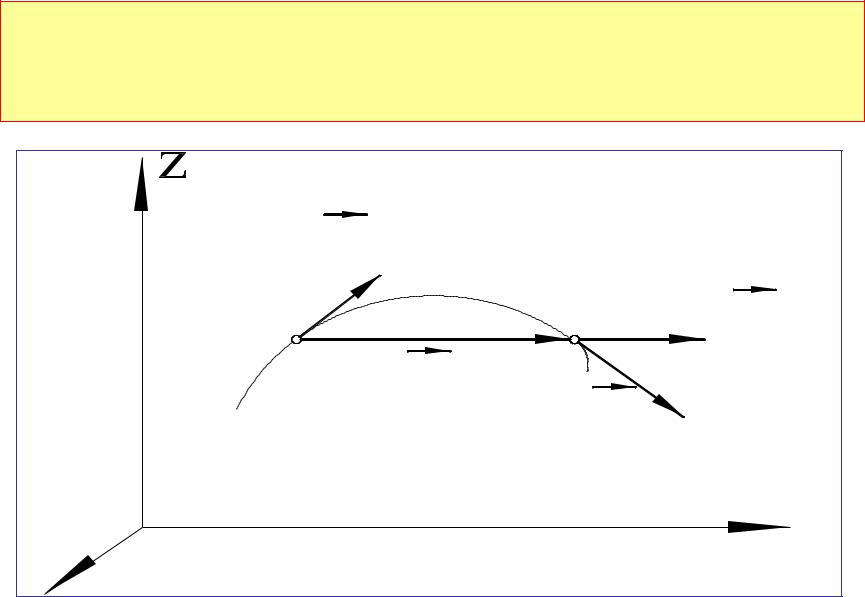
Направление средней и мгновенной |
||
|
|
скоростей |
|
|
|
V 1 |
<V > |
|
1 |
2 |
|
|
|
r |
2 |
|
|
|
|
x |
0 |
|
y |