19. Як змінилося б число днів у році, якщо б Земля оберталася навколо власної осі з тим же періодом, але в протилежному напрямку?

Розв’язок. 

У звичайному році приблизно 365,25 днів (сонячних діб). Оскільки зоряна доба, тривалість якої дорівнює періоду обертання Землі навколо осі, приблизно на 4^m (точніше, в середньому на 3^m56^s) коротша за сонячну, то в році вміщується зоряних діб рівно на одну більше, ніж сонячних, тобто 366,25. При зміні напрямку обертання Землі число зоряних діб у році не зміниться (366,25), адже це число періодів обертання навколо осі за рік, а от тривалість сонячної доби тепер буде меншою за тривалість зоряної на ті ж таки 4^m, оскільки видиме переміщення Сонця серед зір, яке обумовлене річним рухом Землі навколо Сонця, і напрямок добового обертання неба тепер будуть співпадати – кульмінація Сонця наставатиме раніше. Отже, тепер число сонячних діб у році буде на одну більше, ніж зоряних, тобто 367,25.

20. На Меркурії можна було б іноді спостерігати подвійний (повторний) схід або захід Сонця. Дайте пояснення цього незвичного явища.

Розв’язок. 

Як відомо, Меркурій має дуже повільне осьове обертання, тому сонячна доба на цій планеті триває майже два меркуріанських роки. Це означає, що видимий рух Сонця по небу відносно горизонту, який обумовлений накладанням його руху на фоні зір внаслідок переміщення планети по орбіті та її рівномірного осьового обертання досить повільний. Внаслідок значного ексцентриситету еліптичної меркуріанської орбіти швидкість переміщення Сонця на фоні зір може варіюватися в широких межах, що й призводить до описаних в умові завдання явищ.

21. Проникна сила телескопа . Чи можна з його допомогою зареєструвати кульове скупчення із мільйона зір подібних Сонцю, що знаходяться в сусідній галактиці на відстані 10Мпк.

Розв’язок.

За формулою Погсона ( , , 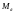– відповідно блиски і абсолютні зоряні величини Сонця й галактики 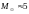) Тоді . Знайдемо видиму величину галактики , – відстань до галактики в парсеках. 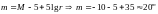. В телескоп галактику не видно

22. В максимумі затемнення змінна зоря має блиск , а в мінімумі . Вважаючи затемнення центральним і супутник темним, знайти відношення об’ємів компонентів цієї пари.

Розв’язок.

В максимумі світить весь диск зорі площею , а в мінімумі – тільки його частина, не закрита супутником, площею . Значить відношення блиску дорівнює . З другого боку відношення за формулою Погсона . Звідси відношення радіусів , а відношення об’ємів

23. Місяць у якийсь із днів знаходився у верхній кульмінації опівдні. Коли він буде кульмінувати наступного дня?

Вказівка: сидеричним, або зоряним Місяцем , називається проміжок часу, протягом якого Місяць здійснює повний оберт навколо Землі і повертається в попереднє положення відносно зірок (T=27,32 доби).

. Сидеричний період Місяця дорівнює 27,32 діб. За одну добу Місяць переміщається на величину

Проходження Місяцем кульмінації буде пізніше на 53 хв.

24. Розрахувати другу космічну швидкість для частинки поблизу нейтронної зорі, якщо її радіус 10 км та маса рівна сонячній масі. Маса Сонця рівна 1,989∙10³⁰ кг. (9 балів)

Відповідь: Параболічна швидкість (друга космічна) V_p= ,

Підставляємо значення G=6.67∙10^-11 Н∙м²/кг²; M =2∙10³⁰ кг; R = 10⁴м

V_p=1,63∙10⁸м/c (Більше половини швидкості світла!)

Бажано перевірити розмірність: (кг∙ м/c²∙м²/кг²∙ кг∙м)^1/2=м/c

25. Скільки має тривати доба на Землі для того, щоб на екваторі нашої планети всі тіла були в стані невагомості? Вважайте, що радіус Землі дорівнює 6400 км.

Для стану невагомості необхідно, щоб прискорення вільного падіння дорівнювало доцентровому прискоренню:

,

де - кутова швидкість обертання Землі навколо осі,

Т- тривалість доби.

Із цих формул знаходимо:

Це формула для періоду коливань математичного маятника, у якого довжина дорівнює радіусу Землі.

Підставляючи числові дані знаходимо: Т=5024 с ≈1,4 години.

26. Приблизно за добу після хромосферного спалаху на Сонці виникає збурення магнітного поля Землі. Зробіть оцінку енергії протонів сонячного вітру, що викликають це збурення. Відповідь дати в електрон-вольтах.

Протони, викинуті під час хромосферного спалаху із Сонця, летять до Землі з постійною швидкістю. Щоб знайти цю швидкість, треба просто поділити відстань від Сонця до Землі на час, за який частинки досягають Землі і який дорівнює одній добі, тому

Тепер нескладно знайти кінетичну енергію протонів, згадавши, що їхня маса дорівнює 1,7∙10^-30 кг. Ця енергія дорівнює 2,5 10^-15 Дж. Для того щоб знайти значення цієї енергії в електрон-вольтах, треба поділити її на заряд електрона в кулонах (1,6 10^-19 Кл) , тому що електрон-вольт — це енергія, якої набуває електрон, пройшовши шлях в електричному полі з різницею потенціалів в 1 В. Одержимо остаточно, що середня енергія протонів сонячного вітру дорівнює приблизно 15 кеВ. Нагадаємо, що електрон-вольт — одиниця енергії, зручна для застосування в атомній фізиці та фізиці елементарних частинок, а в астрофізиці відповідні процеси відіграють важливу роль.

Звернемо увагу на те, що в розрахунках ми отримували не більш ніж дві значущі цифри. Це пов'язано з тим, що насправді різні протони одержують під час спалаху неоднакову енергію, надто під час різних спалахів. Тому йдеться лише про певне середнє, характерне значення енергії протонів і відповідно про середній час досягнення ними Землі. Це підкреслено в умові задачі виразом «приблизно за добу».

27. Від Північного полюса до Південного крізь центр Землі прорита шахта. Один снаряд починає падати в шахту з нульовою початковою швидкістю, а інший запускається на низьку колову орбіту навколо Землі. Який зі снарядів раніше досягне Південного полюса? Чи буде всередині снаряда, що падає в шахті, стан невагомості? Яку швидкість матиме цей снаряд, коли він досягне Південного полюса?

Час досягнення Південного полюса снарядом-супутником Землі визначається як половина періоду його обертання навколо Землі. Щоб знайти цей час, треба довжину півкола πR_З (R_з — радіус Землі) поділити на першу космічну швидкість:

Одержимо, що час

Зауважимо, що формулу для першої космічної швидко­сті нескладно отримати, якщо дорівняти прискорення віль­ного падіння, яке визначається згідно із законом всесвітнього тяжіння як  

доцентровому прискоренню 

Час руху снаряда в шахті визначити складніше. Річ у тому, що в кожний момент він притягується лише тією частиною маси Землі, яка міститься всередині сфери, що проходить через миттєве положення снаряда. Тому першу половину свого шляху снаряд проходить, рухаючись прискорено, але величина прискорення зменшується до нуля в центрі Землі. Закон цього зменшення залежить від змінення величини маси, яка притягує снаряд, а остання, у свою чергу, залежить від закону зміни густини Землі вздовж її радіуса. Але можна відповісти на питання задачі, якщо розглянути прості граничні випадки розподілу густини в планеті, поміж якими знаходиться цей розподіл для реальної Землі.

Випадок 1. Однорідна планета (модель Ньютона) — густина ρ не залежить від відстані до її центра. Тоді на відстані r від центра маса, що притягує снаряд, дорівнює

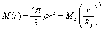
а прискорення снаряда дорівнює відповідно

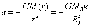
Знак «-» указує на те, що радіус-вектор і вектор прискорення протилежно спрямовані. Але вираз для прискорення показує, що воно за величиною є пропорційним відстані до центра, тобто ми маємо тут справу з таким же законом для сили, як у випадку пружних коливань. Це значить, що півперіод коливання (час, який нам і треба визначити), можна знайти за аналогією до формули для півперіоду малих коливань маятника:

де L — довжина маятника, а g — прискорення вільного падіння на поверхні Землі. Прискорення ж маятника

де r — відхилення маятника від положення рівноваги в горизонтальному напрямку. Порівнюючи вирази для прискорень маятника та нашого снаряда, одержимо, що час руху останнього

Цікаво, що цей час збігається з часом руху супутника по півколу.

 Випадок 2. Уся маса планети зосереджена в її центрі (дуже мале важке ядро й дуже легка оболонка, модель Гюйгенса). У цьому разі потрібний час можна знайти двома шляхами. Перший — це інтегрувати від 0 до R_З рівняння прямолінійного руху з прискоренням 

 другий — розглянути прямолінійний рух снаряда від поверхні до центра Землі як рух за гранично стисненим еліпсом з ексцентриситетом, що дорівнює 1. Те ж стосується й руху снаряда від центра до Південного полюса. Тоді, за третім законом Кеплера, повний час руху снаряда дорівнюватиме періоду руху за еліпсом із великою піввіссю

та відрізнятиметься від випадків Т₁ і Т_2а множником 

.

 Тож ми отримаємо, що час

Час руху снаряда в реальній Землі задовольнятиме нерівність Т_2b<Т₂<Т_2а і буде меншим від часу руху снаряда-супутника за коловою орбітою.

Стан невагомості в снаряді, що рухається в шахті, звичайно, буде, бо вага — це реакція опори, а за будь-якого вільного руху ця реакція відсутня.

До Південного полюса снаряд у шахті прийде з нульовою швидкістю. У першому випадку це випливає з аналогії з маятником, а в загальному випадку — із симетрії задачі відносно центра Землі.

Корисно звернути увагу учнів на те, що прийом, застосований у цій задачі,— знаходження меж, у яких лежить шукана величина,— є досить типовим для фізики й астрономії.