30. Классификация разрывов функций. Разрывы непрерывности функций
Точки разрыва функции |
|
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
|
Непрерывна при x = a. Имеет разрыв при x = a.
Непрерывна при x = a. Имеет разрыв при x = a.
Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
и
правосторонний предел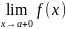 
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов 
называется скачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
31.
Производная функции. Левосторонняя и
правосторонняя производные. Теорема о
существовании производной.
Производная функции
в точке — основное понятие дифференциального
исчисления,
характеризующее скорость изменения
функции (в данной точке). Определяется
как предел отношения
приращения функции к приращению
ее аргумента при
стремлении приращения аргумента к нулю,
если такой предел существует. Процесс
вычисления производной
называется дифференцированием.
Обратный процесс —
нахождение первообразной —интегрирование.
Производная функции 
в
точке
определяется
как предел отношения приращения функции
к приращению аргумента при стремлении
приращения аргумента к нулю:
где 
.
Графически
это тангенс угла наклона касательной
к кривой, изображающей
функцию
.
При
достаточно малых изменениях 
аргумента
выполнено равенство.
В общем случае
именно такая форма определения принимается
за основу для обобщения понятия
производной.
Правой
производной 
функции
в
данной точке
называется
величина:
а левой производной - величина:
если эти пределы существуют.
Для
того чтобы в точке существовала
производная, необходимо и достаточно,
чтобы в точке функция
имела правую и левую производные, и
эти производные были равны между собой:
32. Дифференциал функции. Теорема о дифференцируемости функции в точке. Теорема о связи дифференцируемости и непрерывности функции в точке.
Дифференциалом
функции называется
линейная относительно 
часть
приращения функции. Она обозначается
как 
или 
.
Таким образом:
Теорема
Ферма.
Пусть функция 
определена
на интервале 
и
в некоторой
точке 
имеет
наибольшее или наименьшее значение.
Тогда, если в
точке 
существует
производная, то она равна нулю, то
есть 
.
Доказательство.
Пусть
в точке
максимум
функции, тогда для всех 
выполняется
соотношение 
,
а значит 
.Если 
,
то 
и 
.Если 
,
то 
и 
.Из
существования производной следует,
что 
,
а это возможно, только когда
.Случай,
когда в точке
минимум
функции, доказывается аналогично.
Теорема доказана
Теорема. Если
функция 
дифференцируема
в точке X,
то она и непрерывна в этой точке. Обратное
не гарантировано.
Доказательство. Пусть
функция
Дифференцируема
в точке X.
Это значит, что ее производная 
существует
и конечна в точке X.
То есть
Существует и конечен. По определению предела это значит, что
при 
.
То есть при малых 
имеем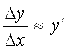 
,
откуда 
,
причем это приближенное равенство тем
точнее, чем меньше
.
Устремляя в нем
,
получаем, что и 
.
А этои означает непрерывность функции
в
точке X.
Первая часть теоремы доказана.
Обратно, если функция непрерывна в некоторой точке X, то это еще не значит, что она дифференцируема в этой точке. Например, функция непрерывна в любой точке X, ибо её график сплошной (без разрывов). И, тем не менее, в точках X1, X2 и X3, как было показано выше, она не дифференцируема.