
- •17. Определение ограниченной и неограниченной функции. Теорема об ограниченной функции, имеющей предел. ?Теорема об ограниченности обратной функции.
- •18. Бесконечно малые и их свойства.
- •19. Основные теоремы о пределах.
- •26. Теорема Вейерштрасса об ограниченности функции на замкнутом промежутке.
- •29. Равномерная непрерывность функции. Теорема Кантора.
- •30. Классификация разрывов функций. Разрывы непрерывности функций
- •32. Дифференциал функции. Теорема о дифференцируемости функции в точке. Теорема о связи дифференцируемости и непрерывности функции в точке.
- •33. Геометрический смысл производной и дифференциала и физический смысл производной.
- •34. Дифференцирование функций
- •35. Правила вычисления производных, связанные с арифметическими действиями над функциями. Производные алгебраической суммы, произведения, частного. Примеры
- •36. Дифференциал суммы, произведения, частного.
- •37. Производная обратной функции
- •38. Производная и дифференциал сложной функции
- •39. Производная и дифференциал неявно заданной функции
- •40. Производная функции, заданной параметрически
- •41. Производная и дифференциал высших порядков. Формула Лейбница.
- •42. Теоремы о дифференцируемых функциях. Определение локального экстремума. Теорема Ферма. Теорема Ролля. Теорема Лагранжа.
- •43. Теорема о возрастании функции. Постоянство функции. Теорема Коши
- •Условие постоянства функции
- •44. Раскрытие неопределенности. Правило Лопиталя
- •45. Формула Тейлора. Теорема Тейлора. Ряд Маклорена
- •Формула Тейлора
- •Остаточный член формулы Тейлора
- •Формулировка теоремы
- •46. Ряды Маклорена для элементарных функций
- •48. Исследование функций. Условие постоянства функции. Признак монотонности функции Исследование функции и построение ее графика
- •49. Отыскание наибольшего и наименьшего значения функции. Критерий существования точек экстремума
- •Необходимое условие экстремума
- •Первое достаточное условие экстремума
- •50. Выпуклость, вогнутость и точки перегиба
- •Теоремы о выпуклости функции и точках перегиба
- •51. Асимптоты графика функции Асимптоты графика функции Виды асимптот
- •52. Общий план исследования функции и построения графика
- •1.Комплексные числа. Сложение и вычитание, умножение и деление кч. Возведение в степень и извлечение корня.
- •Извлечение корня из комплексного числа
- •2.Показательная функция. Формулы Эйлера. Логарифм комплексного числа Показательная функция
- •3.Тригонометрические и гиперболические функции
- •4.Алгебраические многочлены. Теорема Безу. Основная теорема алгебры- теорема Гаусса
- •Формулировка теоремы Безу
- •Следствия из теоремы Безу
- •5. Разложение полинома на множители. Кратные корни. Теорема о необходимом и достаточном условии существовании кратного корня
- •6. Наибольший общий делитель. Алгоритм Евклида
- •Алгоритм Евклида для целых чисел
- •7. Операция освобождения полинома от кратных корней
- •8.Вещественные полиномы. Разложение полинома на множители первой и второй степени.
- •9. Зависимость между корнями алгебраического уравнения и его коэффициентами
- •10. Рациональные алгебраические дроби. Простейшие рац. Дроби
- •11. Разложение правильной рац. Дроби на простейшие
- •3.Геометрическое и механическое истолкование задачи нахождения первообразной ф-ции
- •8. Интегрирование выражений, содержащих радикалы
- •9. Интегрирование биномиальных дифференциалов
- •10. Интегрирование квадратичных иррациональностей подстановками Эйлера
- •11. Другие способы интегрирования иррациональностей
- •12. Интегрирование выражений, содержащих тригонометрические ф-ции
- •13. Тригонометрические подстановки
- •4. Классы интегрируемых функций
- •Свойства определенных интегралов, выраженные неравенствами
- •7 Интеграл с переменным верхним пределом. Теорема Барроу. Формула Ньютона-Лейбница
- •10. Интегрирование четных и нечетных функций в симметричных пределах
- •Формула трапеций
- •1 Несобственный интеграл 1-го рода. Абсолютно сходящиеся интегралы
Билет 1
Величины: постоянные и переменные. Числа: вещественные, рациональные, иррациональные. Область изменения переменной. Промежутки. Абсолютные значения. Неравенства. Окрестность точки.
Переменные величины — это такие величины, которые в условиях данного вопроса могут принимать различные значения
Постоянные величины — это такие величины, которые в условиях данного вопроса сохраняют неизменные значения.
Одни и те же величины в условиях одного вопроса могут быть постоянными, а в другом переменными.
Различие постоянных и переменных величин особенно часто применяется в высшей математике. В элементарной математике основную роль играет разделение величин на известные и неизвестные. Последнее сохраняется и в высшей математике, но не играет там основной роли.
Действительными или вещественными числами называются все положительные числа, отрицательные числа и нуль.
Множество действительных чисел объединяет в себе множество рациональных и иррациональных чисел. Обозначается множество действительных чисел
Рациональное
число (лат. ratio -
отношение, деление, дробь) - это число
которое может быть представлено в виде
дроби ![]() , где числитель
, где числитель ![]() -
целое число, а знаменатель
-
целое число, а знаменатель ![]() -
натуральное. Множество рациональных
чисел
-
натуральное. Множество рациональных
чисел ![]() обозначается
(от англ. quotient "частное")
и может быть записано в виде:
обозначается
(от англ. quotient "частное")
и может быть записано в виде: ![]() .
Числа вида
- называют еще обыкновенными
дробями. Если
.
Числа вида
- называют еще обыкновенными
дробями. Если![]() ,
то дробь
называется правильной, если
,
то дробь
называется правильной, если ![]() ,
то - неправильной.
,
то - неправильной.
Иррациональным числом называется действительное число, которое нельзя представить в виде рациональной дроби .
Множество всех значений, которые может принимать данная переменная, называется областью изменения этой переменной. Это множество и задаёт переменную, то есть формально и является ей.
Промежуток,
или более точно, промежуток числовой
прямой —
множество вещественных
чисел, обладающее тем свойством, что
вместе с любыми двумя числами содержит
любое, лежащее между ними. С
использованием логических
символов, это определение можно
записать так: ![]() —
промежуток, если
—
промежуток, если
![]()
Абсолю́тная
величина́ или мо́дуль числа ![]() —
неотрицательное число, определение
которого зависит от типа числа
.
Обозначается:
—
неотрицательное число, определение
которого зависит от типа числа
.
Обозначается: ![]() .
.
В случае вещественного абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:
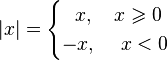
Обобщением
этого понятия является модуль комплексного
числа ![]() ,
также иногда называемый абсолютной
величиной[1].
Он определяется по формуле:
,
также иногда называемый абсолютной
величиной[1].
Он определяется по формуле:
![]()
Неравенство в математике — утверждение об относительной величине или порядке двух объектов (один из объектов меньше или не больше другого), или о том, что два объекта не одинаковы (отрицание равенства). В элементарной математике изучают числовые неравенства, в общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы.
Окрестностью точки называется любой интервал, содержащий эту точку.
Пусть ![]() произвольное
фиксированное число.
произвольное
фиксированное число.
Окрестностью
точки ![]() на
числовой прямой (иногда говорят
на
числовой прямой (иногда говорят ![]() -окрестностью)
называется множество точек, удаленных
от
менее
чем на
,
то есть
-окрестностью)
называется множество точек, удаленных
от
менее
чем на
,
то есть ![]() .
.
Билет 2
Функция. Область определения. Способы задания. Классификация функций. Обратная функция.
Функция ![]() (отображение, операция, оператор) —
это закон или правило,
согласно которому каждому элементу
из
множества
(отображение, операция, оператор) —
это закон или правило,
согласно которому каждому элементу
из
множества ![]() ставится
в соответствие единственный элемент
ставится
в соответствие единственный элемент ![]() из
множества
из
множества ![]() .
.
При этом говорят, что функция задана на множестве , или что отображает в .
Если
элементу ![]() сопоставлен
элемент
сопоставлен
элемент ![]() ,
то говорят, что элемент
находится
в функциональной
зависимости
от
элемента
.
При этом
переменная
называется аргументом функции
или независимой переменной,
множество
называется
областью
задания или областью
определения функции,
а элемент
,
соответствующий конкретному
элементу
— частным
значением функции
в
точке
.
Множество
всех
возможных частных значений
функции
называется
её областью
значений или областью
изменения.
,
то говорят, что элемент
находится
в функциональной
зависимости
от
элемента
.
При этом
переменная
называется аргументом функции
или независимой переменной,
множество
называется
областью
задания или областью
определения функции,
а элемент
,
соответствующий конкретному
элементу
— частным
значением функции
в
точке
.
Множество
всех
возможных частных значений
функции
называется
её областью
значений или областью
изменения.
Функция ![]() есть
множество упорядоченных
пар
есть
множество упорядоченных
пар ![]() ,
которое удовлетворяет следующему
условию: для любого[3]
существует
единственный элемент
такой,
что
,
которое удовлетворяет следующему
условию: для любого[3]
существует
единственный элемент
такой,
что ![]() .
.
Таким
образом, функция —
это упорядоченная
тройка (или кортеж)
объектов ![]() ,
где
,
где
множество называется о́бластьюопределе́ния;
множество называется о́бластьюзначе́ний;
множество упорядоченных пар
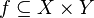 или,
что то же самое, график
функции.
или,
что то же самое, график
функции.
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.
Функция может быть определена разными формулами на разных участках области своего задания.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.
Пример 1: функция E(x) — целая часть числа x. Вообще через E(x) = [x] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, где r — целое число (может быть и отрицательным) и q принадлежит интервалу [0; 1), то [x] = r. Функция E(x) = [x] постоянна на промежутке [r; r+1) и на нем [x] = r.
Пример 2: функция y = {x} — дробная часть числа. Точнее y ={x} = x - [x], где [x] — целая часть числа x. Эта функция определена для всех x. Если x — произвольное число, то представив его в виде x = r + q ( r = [x]), где r — целое число и q лежит в интервале [0; 1), получим {x} = r + q - r=q
Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически.
Характеристики функций (классификация):
Функция ![]() называетсянечётной,
если справедливо равенство
называетсянечётной,
если справедливо равенство
![]()
Функция называетсячётной, если справедливо равенство
![]()
График четной функции симметричен относительно оси Oy, а нечетной – относительно начала координат.
Пусть
дана функция ![]() Тогда
Тогда
функция
называется возраста́ющей на ![]() ,
если
,
если
![]() .
.
функция называется стро́говозраста́ющей на , если
![]() .
.
функция называется убыва́ющей на , если
![]() .
.
функция называется стро́гоубыва́ющей на , если
![]() .
.
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Функция ![]() называется
периодической с пери́одом
называется
периодической с пери́одом ![]() ,
если справедливо
,
если справедливо
![]() .
.
Если
это равенство не
выполнено ни для какого ![]() ,
то функция
называется апериоди́ческой.
,
то функция
называется апериоди́ческой.
Функция ![]() называется ограниченной
сверху на
множестве
называется ограниченной
сверху на
множестве ![]() ,
если существует такое число
,
если существует такое число ![]() ,
что
,
что ![]() для
любого
для
любого ![]() .
.
Замечание. Без ущерба для смысла определения нестрогое неравенство можно заменить на строгое.
Ограничивающее число называется верхней границей или мажорантой функции.
Обра́тнаяфу́нкция — функция,
обращающая зависимость, выражаемую
данной функцией. Например, если функция
от x даёт y,
то обратная ей функция от y даёт x.
Обратная функция функции
обычно
обозначается ![]() ,
иногда также используется обозначение
,
иногда также используется обозначение ![]() .
.
Функция ![]() является
обратной к функции
является
обратной к функции ![]() ,
если выполнены следующие тождества:
,
если выполнены следующие тождества:
![]() для
всех
для
всех ![]()
![]() для
всех
для
всех ![]()
Чтобы найти
обратную функцию, нужно
решить уравнение ![]() относительно
.
Если оно имеет более чем один корень,
то функции обратной к
не
существует. Таким образом, функция
относительно
.
Если оно имеет более чем один корень,
то функции обратной к
не
существует. Таким образом, функция ![]() обратима
на интервале
обратима
на интервале ![]() тогда
и только тогда, когда на этом интервале
она биективна.
тогда
и только тогда, когда на этом интервале
она биективна.
Для непрерывной
функции ![]() выразить
из
уравнения
выразить
из
уравнения ![]() возможно
в том и только том случае, когда
функция
монотонна.
Тем не менее, непрерывную функцию всегда
можно обратить на промежутках её
монотонности. Например,
возможно
в том и только том случае, когда
функция
монотонна.
Тем не менее, непрерывную функцию всегда
можно обратить на промежутках её
монотонности. Например, ![]() является
обратной функцией к
является
обратной функцией к ![]() на
на ![]() ,
хотя на промежутке
,
хотя на промежутке ![]() обратная
функция другая:
обратная
функция другая: ![]() .
.
Билет 3
Метод математической индукции. Неравенство Бернулли. Бином Ньютона.
Метод математической индукции является важным способом доказательства предложений (утверждений), зависящих от натурального аргумента.
Метод математической индукции состоит в следующем:
Предложение (утверждение) P(n), зависящее от натурального числа n, справедливо для любого натурального n если:
P(1) является истинным предложением (утверждением);
P(n) остается истинным предложением (утверждением), если n увеличить на единицу, то есть P(n + 1) - истинное предложение (утверждение).
Таким образом метод математической индукции предполагает два этапа:
Этап проверки: проверяется, истинно ли предложение (утверждение) P(1).
Этап доказательства: предполагается, что предложение P(n) истинно, и доказывается истинность предложения P(n + 1) (n увеличено на единицу).
Нера́венство Берну́лли утверждает:
если ![]() ,
то
,
то
![]() для
всех
для
всех ![]()
Доказательство неравенства проводится методом математической индукции по n. При n = 1 неравенство, очевидно, верно. Допустим, что оно верно для n, докажем его верность для n+1:
![]() ,
,
ч.т.д.
Обобщенное
неравенство Бернулли утверждает,
что при ![]() и
и ![]() :
:
если ![]() ,
то
,
то
если ![]() ,
то
,
то ![]()
при
этом равенство достигается в двух
случаях: ![]()
Бино́мНью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
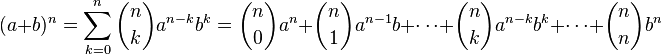
где 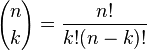 — биномиальные
коэффициенты,
— биномиальные
коэффициенты, ![]() —
неотрицательное целое
число.
—
неотрицательное целое
число.
В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное действительное (или даже комплексное) число. В этом случае бином представляет собой бесконечный ряд.
Формула
бинома Ньютона является частным случаем
разложения функции ![]() в ряд
Тейлора:
в ряд
Тейлора:
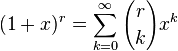 ,
,
где r может быть комплексным числом (в частности, отрицательным или вещественным). Коэффициенты этого разложения находятся по формуле:
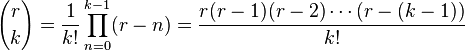
При этом ряд
![]() .
.
сходится
при ![]() .
.
В
частности, при ![]() и
и ![]() получается
тождество
получается
тождество
![]()
Переходя
к пределу при ![]() и
используя второй
замечательный предел
и
используя второй
замечательный предел ![]() ,
выводим тождество
,
выводим тождество
![]()
которое именно таким образом было впервые получено Эйлером.
Билет 4
Множества. Алгебра множеств. Конечное, бесконечное и счетное множества. Ограниченные и неограниченные множества. Наибольшая нижняя и наименьшая верхняя грани множества.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.
Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).
Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.
Например, перечислением заданы следующие множества:
А={1,2,3,5,7} — множество чисел
Х={x1,x2,...,xn} — множество некоторых элементов x1,x2,...,xn
N={1,2,...,n} — множество натуральных чисел
Z={0,±1,±2,...,±n} — множество целых чисел
Множество (-∞;+∞) называется числовой прямой, а любое число — точкой этой прямой. Пусть a — произвольная точка числовой прямой иδ — положительное число. Интервал (a-δ; a+δ) называется δ-окрестностью точки а.
Множество Х ограничено сверху (снизу), если существует такое число c, что для любого x ∈ X выполняется неравенство x≤с (x≥c). Число с в этом случае называется верхней(нижней) гранью множества Х. Множество, ограниченное и сверху и снизу, называется ограниченным. Наименьшая (наибольшая) из верхних (нижних) граней множества называется точной верхней (нижней) гранью этого множества.
В теории
множеств, счётное
мно́жество есть бесконечное
множество,
элементы которого возможно
пронумеровать натуральными
числами.
Более формально:множество
является
счётным, если существует биекция ![]() ,
где
,
где ![]() обозначает
множество всех натуральных чисел.
Другими словами, счётное множество —
это множество, равномощное множеству
натуральных чисел.
обозначает
множество всех натуральных чисел.
Другими словами, счётное множество —
это множество, равномощное множеству
натуральных чисел.
Счётное
множество является «наименьшим»
бесконечным множеством, то есть в любом
бесконечном множестве найдётся счётное
подмножество. Мощность
множествавсех
натуральных чисел обозначается
символом ![]() (произносится:
"алеф-нуль").
(произносится:
"алеф-нуль").
Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным.
Алгебра множеств
Объединением
(суммой) двух множеств A и B называется
множество (его принято обозначать ![]() ) состоящее
из всех тех и только тех элементов,
которые принадлежат хотя бы одному из
этих множеств - либо A, либо B.
) состоящее
из всех тех и только тех элементов,
которые принадлежат хотя бы одному из
этих множеств - либо A, либо B.
![]()
Пересечением
(произведением) двух множеств A и B
называется множество (его принято
обозначать ![]() ) состоящее
из всех тех и только тех элементов,
которые принадлежат каждому из множеств
A и B.
) состоящее
из всех тех и только тех элементов,
которые принадлежат каждому из множеств
A и B.
![]()
Разностью двух множеств A и B называется множество (его обычно обозначают A\B или A-B), состоящее из тех и только тех элементов, которые принадлежат множеству A и не принадлежат множеству B.
|
Симметрической
разностью множеств A и B называется
множество обозначаемое через A ![]() B
и определяемое следующим образом:
B
и определяемое следующим образом:
|
Билет 5
Понятие числовой последовательности. Классификация последовательностей
Последовательностью называется
функция, которая переводит
множество натуральных
чисел ![]() в
некоторое множество
в
некоторое множество ![]() :
: ![]()
Элемент ![]() называется первым
членом последовательности,
называется первым
членом последовательности, ![]() -
вторым, ... ,
-
вторым, ... , ![]() -
-ым
или общим
членом последовательности.
-
-ым
или общим
членом последовательности.
Последовательность ![]() называется ограниченной
сверху,
если существует такое число
называется ограниченной
сверху,
если существует такое число ![]() ,
что для любого номера
,
,
что для любого номера
, ![]()
Последовательность
называется ограниченной
снизу,
если существует такое число ![]() ,
что для любого номера
,
,
что для любого номера
, ![]()
Последовательность
называется ограниченной,
если она ограниченная сверху и ограниченная
снизу, то есть существует такое число ![]() ,
что для любого номера
,
,
что для любого номера
, ![]()
Последовательность
называется неограниченной,
если существует такое число
,
что существует такой номер
,
что ![]()
Последовательность
называется монотонно
возрастающей,
если для любого ![]() ,
, ![]()
Последовательность
называется монотонно
возрастающей,
если для любого
, ![]()
Последовательность
называется монотонно
убывающей,
если для любого
, ![]()
Или,
Последовательность
называется монотонно
убывающей,
если для любого
, ![]()
Билет 6
Предел последовательности. Теорема о единственности предела. Сходящиеся и расходящиеся последовательности. Свойства ограниченных последовательностей.
Число ![]() называется пределом
последовательности
и
обозначается
называется пределом
последовательности
и
обозначается ![]() ,
,![]()
Число
называется пределом
последовательности
,
если для любого ![]() существует
номер
существует
номер![]() такой,
что для любого
такой,
что для любого ![]() выполняется
неравенство
выполняется
неравенство ![]() :
:
![]()
Если
функция ![]() в
точке
в
точке ![]() имеет
предел, то этот предел единственный
имеет
предел, то этот предел единственный
Последовательность, которая имеет предел, называется сходящейся; иначе - расходящейся.
Сходящаяся последовательность имеет только один предел.
Последовательность называется ограниченной сверху, если существует такое число , что для любого номера ,
Последовательность называется ограниченной снизу, если существует такое число , что для любого номера ,
Последовательность называется ограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число , что для любого номера ,
Последовательность называется неограниченной, если существует такое число , что существует такой номер , что
Свойства ограниченных последовательностей
Ограниченная сверху числовая последовательность имеет бесконечно много верхних граней.
Ограниченная снизу числовая последовательность имеет бесконечно много нижних граней.
Ограниченная последовательность имеет по крайней мере одну предельную точку.
У ограниченной последовательности существуют верхний и нижний пределы.
Для любого наперёд взятого положительного числа все элементы ограниченной числовой последовательности
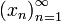 ,
начиная с некоторого номера, зависящего
от
,
лежат внутри интервала
,
начиная с некоторого номера, зависящего
от
,
лежат внутри интервала 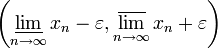 .
.Если за пределами интервала
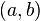 лежит
лишь конечное число элементов ограниченной
числовой последовательности
,
то интервал
лежит
лишь конечное число элементов ограниченной
числовой последовательности
,
то интервал 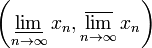 содержится
в интервале
.
содержится
в интервале
.Справедлива теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Билет 7
Точная верхняя и нижняя границы последовательностей. Теорема Вейерштрасса
Точной
(наименьшей) верхней гранью (границей),
или супре́мумом (лат. supremum —
самый высокий) подмножества
упорядоченного
множества (или класса)
,
называется наименьший элемент
,
который равен или больше всех
элементов множества
.
Другими словами, супремум — это
наименьшая из всех верхних граней.
Обозначается ![]() .
.
Более формально:
![]() —
множество верхних
граней
,
то есть элементов
,
равных или больших всех элементов
—
множество верхних
граней
,
то есть элементов
,
равных или больших всех элементов
![]()
Точной
(наибольшей) нижней гранью (границей),
или и́нфимумом (лат. infimum —
самый низкий) подмножества
упорядоченного
множества (или класса)
,
называется наибольший элемент
,
который равен или меньше всех
элементов множества
.
Другими словами, инфимум — это
наибольшая из всех нижних граней.
Обозначается ![]() .
.
Мажоранта или верхняя
грань (граница) числового
множества
—
число ![]() ,
такое что
,
такое что ![]() .
Миноранта или нижняя
грань (граница) числового
множества
—
число
.
Миноранта или нижняя
грань (граница) числового
множества
—
число ![]() ,
такое что
,
такое что ![]() .
.
Теорема Вейерштрасса. (Основная теорема теории последовательностей).
Если последовательность является нестрого возрастающей (нестрого убывающей) и ограничена сверху (снизу), то является сходящейся.
Данную теорему можно сформулировать немного иначе - Любая монотонная и ограниченная последовательность имеет предел.
Билет 8
Определение бесконечно большой и бесконечно малой последовательности
Последовательность
называется бесконечно
малой последовательностью (б.м.п.),
если для любого
существует
номер ![]() такой,
что для любого
такой,
что для любого ![]() выполняется
неравенство:
выполняется
неравенство:![]()
Последовательность
называется бесконечно
большой (б.б.п.),
если для любого ![]() существует
номер
такой,
что для любого
выполняется
неравенство:
существует
номер
такой,
что для любого
выполняется
неравенство: ![]()
Основные свойства б.м. и б.б. последовательностей
1° Сумма б.м. последовательностей есть б.м.п.
2° Произведение ограниченной последовательности и б.м. есть б.м.п.
3° Если -б.м.п., то - ограниченная последовательность.
4° Произведение б.м.п. есть последовательность б.м.
5°
Если
-б.м.п.
и ![]() ,
то
,
то ![]() ,
т.е.
,
т.е. ![]()
6°
Если
-б.м.п.
и ![]() ,
то последовательность
,
то последовательность ![]() -
б.б.п.
-
б.б.п.
7°
Если
-б.б.п.,
то ![]() и
последовательность
-
б.м.п.
и
последовательность
-
б.м.п.
Билет 10
Неопределенные выражения
Неопределенные
выражения (неопределенности). Иногда
при формальной подстановке числа а вместо
аргумента х под
знак функции у = f(x) и
дальнейшем проведении алгебраических
действий над получившимся выражением
или при переходе к пределу получаются
выражения типа:
![]() (*)
(*)
Эти выражения бессмысленны с алгебраической точки зрения. Иногда, исходя из понятий математического анализа, таким выражениям удается придать определенный удобный смысл.
Чаще всего,
в случае непрерывности функции у = f(x)
в некоторой окрестности точких = а,
исключая саму эту точку, под f(a)
понимают ![]() .
.
Более того, неопределенные выражения часто возникают при вычислении пределов функций, построении графиков и т.д. В этих случаях имеется ряд приемов «раскрытия неопределенностей».
Иногда неопределенными называют выражения, предел которых не может быть найден путем непосредственного применения теорем о пределе.
Основными инструментами для раскрытия неопределённостей служат: формула Тейлора,первый замечательный предел, второй замечательный предел, правило Лопиталя и т.п.
Билет 11
Определение последовательности. ТеоремаБольцано-Вейерштрасса
Последовательностью называется функция, которая переводит множество натуральных чисел в некоторое множество :
Элемент называется первым членом последовательности, - вторым, ... , - -ым или общим членом последовательности.
Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер.
Другим
способом задания последовательности
является задание последовательности
с помощью рекуррентного соотношения.
В этом случае задается один или несколько
первых элементов последовательности,
а остальные определяются по некоторому
правилу. Например, известен первый
член
последовательности
и известно, что ![]() ,
то есть
,
то есть ![]() и
так далее до нужного члена.
и
так далее до нужного члена.
Теорема Больцано-Вейерштрасса (или лемма Больцано-Вейерштрасса о предельной точке).
Из всякой ограниченной
последовательности точек
пространства ![]() можно
выделить сходящуюся подпоследовательность.
можно
выделить сходящуюся подпоследовательность.
Так как последовательность
ограничена, то она имеет хотя бы одну
предельную точку ![]() .
В таком случае из этой последовательности
можно выделить подпоследовательность,
сходящуюся к точке
.
.
В таком случае из этой последовательности
можно выделить подпоследовательность,
сходящуюся к точке
.
Из любой ограниченной последовательности можно выделить монотонную подпоследовательность.
Действительно, согласно теореме Больцано-Вейерштрасса, из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность, а из этой подпоследовательности можно выделить монотонную подпоследовательность.
Пусть
-
ограниченная последовательность,
элементы которой принадлежат промежутку ![]() .
Тогда предел
.
Тогда предел ![]() любой
сходящейся подпоследовательности
любой
сходящейся подпоследовательности ![]() этой
последовательности также находится на
сегменте
.
этой
последовательности также находится на
сегменте
.
Билет 12
Критерий Коши сходимости последовательностей
В математике сходимость означает существование конечного предела у числовой последовательности или суммы бесконечного ряда или несобственного интеграла. Соответственно, расходимость — отсутствие конечного предела.
Из
определения сходимости последовательности ![]() к
точке a вытекает, что для любого
интервалом
длиной 2
можно
накрыть всю эту последовательность,
исключением может быть конечное число
ее элементов, если середину интервала
поместить в точке
.
Справедливо и обратное : если
последовательность
такова,
что для любого
можно
накрыть всю эту последовательность,
исключая может быть конечное число ее
элементов, поместив центр интервала в
некоторую точку, то она сходится.
Сформулируем это утверждение более
точно.
к
точке a вытекает, что для любого
интервалом
длиной 2
можно
накрыть всю эту последовательность,
исключением может быть конечное число
ее элементов, если середину интервала
поместить в точке
.
Справедливо и обратное : если
последовательность
такова,
что для любого
можно
накрыть всю эту последовательность,
исключая может быть конечное число ее
элементов, поместив центр интервала в
некоторую точку, то она сходится.
Сформулируем это утверждение более
точно.
Определение. Подпоследовательность ![]() называется последовательностью
Коши или фундаментальной,
если
называется последовательностью
Коши или фундаментальной,
если ![]()
Последовательность
называется фундаментальной,
если для ![]() существует
номер
такой,
что для любых
существует
номер
такой,
что для любых ![]() выполняется
неравенство:
выполняется
неравенство: ![]()
Если последовательность фундаментальная, тогда существует такой номер , что в
 -окрестности
точки
-окрестности
точки содержатся
все члены последовательности, начиная
с этого номера.
содержатся
все члены последовательности, начиная
с этого номера.Последовательность сходится тогда и только тогда, когда она ограниченная и верхний предел равен нижнему.
Теорема ( Критерий Коши ). Для того, чтобы последовательность сходилась, необходимо и достаточно чтобы она была фундаментальной.
Билет 13
Число е
e — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».
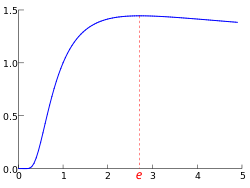
Максимум
функции ![]() достигается
при
достигается
при ![]() .
.
Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.
Поскольку
функция экспоненты ![]() интегрируется
и дифференцируется «в саму
себя», логарифмы именно
по основанию e принимаются
как натуральные.
интегрируется
и дифференцируется «в саму
себя», логарифмы именно
по основанию e принимаются
как натуральные.
Число e может быть определено несколькими способами.
Через предел:
![]() (второй замечательный
предел).
(второй замечательный
предел).
Как сумма ряда:
![]() или
или ![]() .
.
![]()
Как единственное число a, для которого выполняется
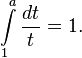
Как единственное положительное число a, для которого верно
![]()
![]() Данное
свойство играет важную роль в решении
дифференциальных уравнений. Так,
например, единственным решением
дифференциального уравнения
Данное
свойство играет важную роль в решении
дифференциальных уравнений. Так,
например, единственным решением
дифференциального уравнения ![]() является
функция
является
функция ![]() ,
где c —
произвольная константа.
,
где c —
произвольная константа.
![]()
Билет 14
Предел функции. Определение окрестности предела. Определение предела по Гейне на языке последовательностей. Определение предела по Коши. Теорема о равносильности определений по Гейне и по Коши
Преде́лфу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
Определение по Гейне (на языке последовательностей):
Значение ![]() называется пределом (предельным
значением)
функции
называется пределом (предельным
значением)
функции ![]() в
точке
,
если для любой последовательности точек
в
точке
,
если для любой последовательности точек ![]() ,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции ![]() сходится
к
сходится
к
Определение по Коши:
Значение
называется пределом (предельным
значением)
функции
в
точке
,
если для любого наперёд взятого
положительного числа
найдётся
отвечающее ему положительное число ![]() такое,
что для всех аргументов
,
удовлетворяющих условию
такое,
что для всех аргументов
,
удовлетворяющих условию ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .
.
![]()
Все данные выше определения предела функции в точке эквивалентны. Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных.
Билет 15
Односторонние пределы. Теорема о существовании предела
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Число ![]() называется правым
пределом функции
называется правым
пределом функции ![]() в
точке
,
если для
в
точке
,
если для
![]() такое,
что для любого
такое,
что для любого ![]() и
и ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() (рис.
1). Правый предел обозначается
(рис.
1). Правый предел обозначается ![]()
Число
называется левым
пределом функции
в
точке
,
если для
такое,
что для любого
и ![]() ,
выполняется неравенство
(рис.
2). Левый предел обозначается
,
выполняется неравенство
(рис.
2). Левый предел обозначается ![]()
Левый и правый пределы функции называются односторонними пределами.
Если существуют ![]() и
и ![]() ,
причем
,
причем ![]() ,
то существует и
,
то существует и ![]() .
Обратное утверждение также верно.
.
Обратное утверждение также верно.
В случае, если ![]() ,
то предел
,
то предел ![]() не
существует.
не
существует.
Признаки существования пределов:
(О пределе промежуточной функции).
Если имеет место
соотношение ![]() и
,
и
, ![]() ,
то и
,
то и ![]()
(О пределе монотонной функции).
Если функция
является
монотонной и ограниченной в области ![]() или
или ![]() ,
то соответственно существует ее левый
предел
или
ее правый
предел
.
,
то соответственно существует ее левый
предел
или
ее правый
предел
.
Ограниченная монотонная последовательность имеет предел.
Билет 16
Критерий Коши о существовании предела
Для того чтобы
функция f, x ![]() X, имела
в (конечной
или бесконечно удаленной) точке x0 конечный
предел, необходимо
и достаточно, чтобы
для любого
X, имела
в (конечной
или бесконечно удаленной) точке x0 конечный
предел, необходимо
и достаточно, чтобы
для любого ![]() >
0 существовала
такая окрестность
U(x0) точки x0, что
для любых x'
X
>
0 существовала
такая окрестность
U(x0) точки x0, что
для любых x'
X ![]() U(x0) и x"
X
U(x0)
выполнялось бы неравенство
U(x0) и x"
X
U(x0)
выполнялось бы неравенство
| f(x") - f(x')|< . |
(6.39) |
![]() Докажем
необходимость условия (6.39). Пусть
Докажем
необходимость условия (6.39). Пусть ![]() f(x)
= a
R,
тогда для любого
>
0 существует такая окрестность U(x0)
точки x0,
что для каждого x
X
U(x0)
справедливо неравенство
f(x)
= a
R,
тогда для любого
>
0 существует такая окрестность U(x0)
точки x0,
что для каждого x
X
U(x0)
справедливо неравенство
| f(x) -a| < /2.
Поэтому если x' X U(x0) и x" X U(x0), то
| f(x") - f(x')| = |[f(x") - a] + [a - f(x')]| < < |f(x") - a| + |a - f(x')| < /2 + /2 = .
Докажем
достаточность условий (6.39) для
существования конечного предела
f(x).
Пусть произвольно фиксировано
>
0; тогда существует такая окрестность U(x0),
что для всех x'
X
U(x0)
и всех
x"
X
U(x0)
выполняется неравенство | f(x") - f(x')|
<
.
Возьмем какую-либо
последовательность xn![]() x0, xn
X, n = 1,
2, ... В силу определения предела
последовательности существует такой
номер n0,
что для всех
n > n0 имеет
место включение xn
U(x0),
а поскольку xn
X,
то и включение xn
X
U(x0).
Тогда для всех номеров n > n0 и m > n0 будем
иметь xn
X
U(x0), xm
X
U(x0),
и, следовательно, будет выполняться
неравенство | f(xn) - f(xm)|
<
.
Это означает, что последовательность
{ f(xn)}
удовлетворяет критерию сходимости Коши
для последовательностей и, следовательно,
имеет конечный предел.
Таким образом, для любой
последовательности xn
x0, xn
X, n = 1,
2, ..., последовательность { f(xn)}
имеет конечный предел. Отсюда в силу леммы
2 п. 6.4
сразу следует, что функция fимеет
в точке x0 конечный
предел.
x0, xn
X, n = 1,
2, ... В силу определения предела
последовательности существует такой
номер n0,
что для всех
n > n0 имеет
место включение xn
U(x0),
а поскольку xn
X,
то и включение xn
X
U(x0).
Тогда для всех номеров n > n0 и m > n0 будем
иметь xn
X
U(x0), xm
X
U(x0),
и, следовательно, будет выполняться
неравенство | f(xn) - f(xm)|
<
.
Это означает, что последовательность
{ f(xn)}
удовлетворяет критерию сходимости Коши
для последовательностей и, следовательно,
имеет конечный предел.
Таким образом, для любой
последовательности xn
x0, xn
X, n = 1,
2, ..., последовательность { f(xn)}
имеет конечный предел. Отсюда в силу леммы
2 п. 6.4
сразу следует, что функция fимеет
в точке x0 конечный
предел. ![]()
Замечание.
Сформулируем критерий Коши существования
конечного предела функции в терминах
неравенств для случая, когда x0 -
действительное число: функция f, x
X, имеет
в точке x0
R конечный
предел тогда и только тогда, когда
для любого
>
0 существует
такое ![]() >
0, что для всех
точек
x'
X, x"
X,
|x' - x0|
<
,
|x" - x0|
<
, выполняется
неравенство | f(x") - f(x')|
<
.
>
0, что для всех
точек
x'
X, x"
X,
|x' - x0|
<
,
|x" - x0|
<
, выполняется
неравенство | f(x") - f(x')|
<
.
17. Определение ограниченной и неограниченной функции. Теорема об ограниченной функции, имеющей предел. ?Теорема об ограниченности обратной функции.
Пусть
задана функция y=f(x), определенная на
некотором множестве D значений
аргумента.
Функция
y=f(x) называется ограниченной
на множестве D, если существует
положительное число М такое, что для
всех значений x из рассматриваемого
множества, выполняется неравенство
|f(x)|≤M. Если же такого числа М не существует,
то функция f(x) называется неограниченной
на множестве D.
Пример:
Функция
y=sin x, определенная при -∞<x<+∞,>0, что
при всех значениях х, удовлетворяющих
неравенству |x|>N, функция f(x) ограничена.
Если
функция f(x) имеет предел в точке a ![]() ,то
она ограничена в некоторой окрестности
точки a.
Доказательство:
,то
она ограничена в некоторой окрестности
точки a.
Доказательство:
Пусть
,
тогда ![]() ,
отсюда
получаем
,
отсюда
получаем ![]() .
Обратное неверно.
.
Обратное неверно.
Контрольный
пример:
![]() в
окрестности точки 0.
в
окрестности точки 0.
![]() –
не существует.
–
не существует.
18. Бесконечно малые и их свойства.
Функция y=f(x) называется бесконечно
малой при x→a или
при x→∞,
если ![]() или
или ![]() ,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
,
т.е. бесконечно малая функция – это
функция, предел которой в данной точке
равен нулю.
П римеры.
римеры.
Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как
 (см.
рис.).
(см.
рис.).Функция f(x) = tgx – бесконечно малая при x→0.
f(x) = ln (1+x)– бесконечно малая при x→0.
f(x) = 1/x– бесконечно малая при x→∞. Основные свойства бесконечно малых функций (б.м.)
1°
Сумма конечного числа б.м. функций
является функцией бесконечно малой.
2°
Произведение б функции на ограниченную
есть функция бесконечно малая.
3°
Произведение двух б.м функций есть
функция бесконечно малая..
4°
Произведение б.м функции на константу
является бесконечно малой функцией.
5°
Частное от деления б.м функции на
функцию, предел которой
не равен нулю, есть функция бесконечно
малая.
6° Функция ![]() ,
обратная к б.м функции
,
обратная к б.м функции ![]() ,
есть функция бесконечно большая. Верно
и обратное.
,
есть функция бесконечно большая. Верно
и обратное.
19. Основные теоремы о пределах.
Теорема
1. Предел
суммы равен сумме пределов, если
они
существуют: ![]()
Доказательство:
![]()
![]() Из
теоремы о связи между пределом и
бесконечно малой величиной
следует:
Из
теоремы о связи между пределом и
бесконечно малой величиной
следует:
![]()
![]()
![]() Получаем
Получаем ![]()
![]()
Теорема
2. Предел
произведения равен произведению
пределов, если они
существуют: ![]() Доказательство:
Доказательство:
![]()
![]() Из
теоремы о связи между пределом и
бесконечно малой величиной
следует:
Из
теоремы о связи между пределом и
бесконечно малой величиной
следует:![]()
![]() Получаем
Получаем ![]()
![]()
![]() Теорема
3. Предел
частного равен частному пределов:
Теорема
3. Предел
частного равен частному пределов:  .
При
условии: все пределы существуют
и
.
При
условии: все пределы существуют
и ![]() .
Доказательство:
.
Доказательство:
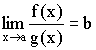
![]() Из
теоремы о связи между пределом и
бесконечно малой величиной
следует:
Из
теоремы о связи между пределом и
бесконечно малой величиной
следует:
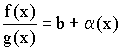 ;
Получаем:
;
Получаем: 

Теорема
4. Предел
сохраняет знак неравенства. Если ![]()
![]() .
.
Доказательство:
![]() Следовательно,
Следовательно, ![]()
![]() Следствие:
Следствие:

Теорема
5. Если
функция ограниченна и монотонна на
(a, b), то она имеет предел: ![]()
20-21.
Первый и второй замечательные пределы
и следствия.
Теорема. Первый
замечательный предел ![]() .
Доказательство (геометрическое):
.
Доказательство (геометрическое):
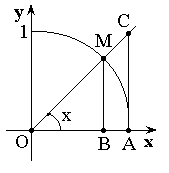
![]()
![]()
![]()
![]()
![]()


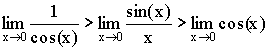 Так
как
Так
как 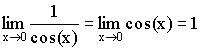 ,
то
.
,
то
.
Следствия из теоремы:
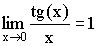 2)
2)  3)
3) 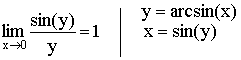 4)
4) 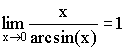 5)
5) 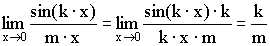 Теорема. Второй
замечательный предел
Теорема. Второй
замечательный предел 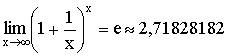 .
Доказательство:
Бином
Ньютона:
.
Доказательство:
Бином
Ньютона:
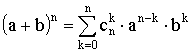 ,
где
,
где 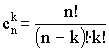 .
Используем
бином Ньютона для доказательства
неравенства:
.
Используем
бином Ньютона для доказательства
неравенства: 
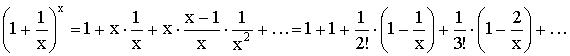 Отсюда
заключаем, что
,
а значит
Отсюда
заключаем, что
,
а значит  .
Следствия
из теоремы:
1)
.
Следствия
из теоремы:
1) 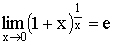 2)
2) 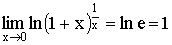 3)
3)  4)
4) 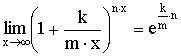
22.
Сравнения бесконечно малыхвеличин
(б.м.в.) Эквивалентные бесконечно
малые.
Пусть ![]() –
бесконечно малые величины при
–
бесконечно малые величины при ![]() ,
т.е.
,
т.е. ![]() .
Определение
1. Если
.
Определение
1. Если  ,
то
–
б.м.в. одного порядка малости.
Определение
2. Если
,
то
–
б.м.в. одного порядка малости.
Определение
2. Если  ,
то
,
то ![]() –
б.м.в. более высокого порядка,
чем
–
б.м.в. более высокого порядка,
чем ![]() .
.
![]() –
– ![]() более
высокого порядка, чем
более
высокого порядка, чем ![]() ("о"
– читается как "о малое").
("о"
– читается как "о малое").
![]() –
более
низкого порядка, чем
("О"
– читается как "О большое").
Определение
3. Если
–
более
низкого порядка, чем
("О"
– читается как "О большое").
Определение
3. Если  ,
то
и
эквивалентны
–
,
то
и
эквивалентны
– ![]() .
Следствие
из определения 3:
.
Следствие
из определения 3: ![]() при
при ![]() Теорема. Если
и
эквивалентны
(
Теорема. Если
и
эквивалентны
(![]() )
, то
)
, то ![]() и
и ![]() Доказательство:
Пусть
–
бесконечно малые величины при
и
они эквивалентны
).
Тогда
Доказательство:
Пусть
–
бесконечно малые величины при
и
они эквивалентны
).
Тогда 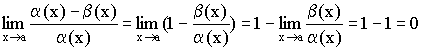 .
Б.м.
функции
.
Б.м.
функции ![]() и
и ![]() называются эквивалентными или равносильными
б.м. одного порядка при
называются эквивалентными или равносильными
б.м. одного порядка при ![]() ,
если
,
если ![]() Обозначают:
Обозначают: ![]() при
.
при
.
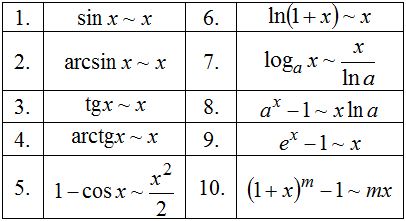
25. Непрерывность функции. Определение непрерывности функции в точке и на промежутке. Теорема об арифметических действиях над непрерывными функциями. Непрерывность сложной функции. Ограниченность непрерывной функции.
Функция, непрерывная во
всех точках некоторой области,
называется непрерывной
в этой области.
Функция
называется непрерывной
справа в точке
,
если ![]() .
Функция
называется непрерывной
слева в точке
,
если
.
Функция
называется непрерывной
слева в точке
,
если ![]() .
Функция
.
Функция ![]() называется непрерывной
в интервале
называется непрерывной
в интервале ![]() ,
если она непрерывна в каждой точке этого
интервала.
Функция
называется непрерывной
на отрезке
,
если она является непрерывной в
интервале
,
непрерывной справа в точке
,
то есть
,
если она непрерывна в каждой точке этого
интервала.
Функция
называется непрерывной
на отрезке
,
если она является непрерывной в
интервале
,
непрерывной справа в точке
,
то есть ![]() и
непрерывной слева в точке
,
то есть
и
непрерывной слева в точке
,
то есть ![]() .
Теорема
об арифметических действиях:
Если
функция f(x)-
непрерывна в т. x0, j(x)
непрерывна в т. x0,
тогда:
1) f(x) ± j(x)
- непрерывная функция в т. x0,
2) f×j -
непрерывная функция в т. x0,
3) f/j, j(x0)¹0
- непрерывно в т. x0.
.
Теорема
об арифметических действиях:
Если
функция f(x)-
непрерывна в т. x0, j(x)
непрерывна в т. x0,
тогда:
1) f(x) ± j(x)
- непрерывная функция в т. x0,
2) f×j -
непрерывная функция в т. x0,
3) f/j, j(x0)¹0
- непрерывно в т. x0.
