Тема 3: Математичні методи розв’язання інженерних задач

Чисельні (математичні) методи дозволяють звести розв’язання задачі до кінцевого числа арифметичних дій, при цьому результат отримують у вигляді числового значення. В теперішній час є основним інструментом для розв’язання складних інженерних задач. Чисельні методи є наближеними і дозволяють розв’язувати задачі із деякою (заданою) точністю δ.

Ітераційні методи розв’язання задач – методи, за якими розв’язок шукають методом послідовних наближень (циклів обчислень, ітерацій). Значення невідомого в кожному наступному наближенні розраховують за рекурентними формулами.

3.1. Розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) ітераційними методами

Задача 10. При розрахунку аркових гребель за методом арок центральної консолі (рис.3.1) величина прогину ω(у) може бути знайдена із розв’язання диференціального рівняння прогину консолі на пружній основі [7]

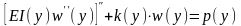, (3.9)

де ЕІ(у) – жорсткість консолі; k(y) – коефіцієнт постелі;

p(y) – гідростатичне навантаження.

Рис.3.1. Схема до розрахунку аркової греблі методом арок центральної консолі

При розв’язанні рівняння (3.9) методом скінченних різниць отримують СЛАР. Припустимо, що отримана СЛАР має одну з форм, зазначених в табл.3.1. Розв’язати СЛАР ітераційними методами. Точність δ=0,05.

Таблиця 15

№ вар.	СЛАР	Схема перетворення СЛАР
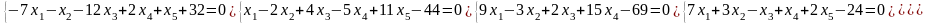
1		Поміняти рівняння між собою місцями

Розв’язання задачі 10 :

Таблиця 16

k	х1	х2	х3	х4	х5	δ( х1)	δ( х2)	δ( х3)	δ( х4)	δ( х5)
1	3,429	0,600	2,667	4,600	2,941
2	2,055	1,989	1,628	2,307	5,227	-0,401	2,315	-0,389	-0,498	0,777
3	0,986	1,792	2,122	3,548	4,475	-0,520	-0,099	0,303	0,538	-0,144
4	1,178	1,887	2,906	4,084	4,783	0,195	0,053	0,369	0,151	0,069
5	1,085	2,004	2,901	3,883	5,030	-0,079	0,062	-0,002	-0,049	0,052
6	0,992	1,988	2,933	3,963	4,966	-0,085	-0,008	0,011	0,021	-0,013
7	1,010	1,991	2,996	4,011	4,983	0,018	0,002	0,022	0,012	0,003

Таблиця 17

k	х1	х2	х3	х4	х5	δ( х1)	δ( х2)	δ( х3)	δ( х4)	δ( х5)
1	3,429	0,600	2,667	4,600	2,941
2	2,055	1,928	2,319	3,443	4,896	-0,401	2,213	-0,130	-0,251	0,665
3	1,043	1,910	2,881	3,972	4,976	-0,493	-0,009	0,242	0,154	0,016
4	1,033	2,000	2,974	3,984	4,998	-0,010	0,047	0,032	0,003	0,004

Відповідь: За методом простої ітерації із точністю δ =0,05, розв’язками системи є: х₁=1,010; х₂=2,996; х₃= 4,011; за методом Зейделя: х₁=1,033; х₂=2,000; х₃= 2,974.

Лабораторна робота № 11