2. Ввести вихідні дані.
Групи рівноточних вимірювань (вибірки) обробляються відповідно до п.3 задачі 2. Для кожної із груп вимірювань визначають оцінки параметрів закону розподілу: математичного сподівання за формулою (1.1) та дисперсії D(x) за формулою (1.3).
Обчислюють значення критерію Кохрана за формулою (1.10).
Перевіряють гіпотезу про однорідність дисперсій за умовою (1.11).
Якщо гіпотеза про однорідність дисперсій підтверджується, визначають оцінку середньої дисперсії
.
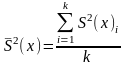(1.12)
Таблиця 7
№з/п |
V |
h 1 |
h 2 |
h 3 |
|||
|
Варіант 1 |
||||||
1 |
0 |
53,1 |
54,5 |
53,5 |
|
||
2 |
1 |
42,8 |
43,6 |
42,6 |
|
||
3 |
2 |
35,5 |
36,1 |
35,8 |
|
||
4 |
3 |
26,9 |
25,8 |
26,1 |
|
||
5 |
4 |
14,7 |
15,2 |
15,8 |
|
||
Статистичну обробку даних проведено у вигляді табл. 8.
Значення
G
– критерію Кохрана
.
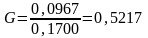Табличне значення критерію Кохрана при кількості ступенів вільності f=2; k=5 G0.05=0,6838.
Таблиця 8
№з/п |
v |
h1 |
h2 |
h3 |
hcep |
S |
D |
1 |
0 |
53.1 |
54.5 |
53.5 |
57.3 |
0.721 |
0.520 |
2 |
1 |
42.8 |
43.6 |
42.6 |
43 |
0.529 |
0.280 |
3 |
2 |
35.5 |
35.8 |
35.8 |
35.8 |
0.3 |
0.090 |
4 |
3 |
26.9 |
26.1 |
26.1 |
26.267 |
0.569 |
0.323 |
5 |
4 |
14.7 |
15.8 |
15.8 |
15.233 |
0.551 |
0.303 |
|
|
|
|
|
|
|
0,997 |
|
|
|
|
|
|
|
1,517 |
0,5686<0,5981 - умова (1.11) виконується; гіпотеза про однорідність дисперсій приймається.
Середня
дисперсія
.
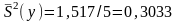Відповідь:
Дисперсії груп вимірювань можна вважати
однорідними. Оцінка середньої дисперсії
.
Лабораторна робота №4
Середньоквадратичне відхилення результату непрямих вимірювань
Якщо
деяка величина z
залежить від ряду незалежних величин
,
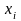
середньоквадратичні відхилення яких
відомі, середньоквадратичне відхилення
цієї величини визначають за залежністю
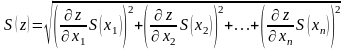(1.13)
де
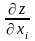– часткові похідні від функції
по її аргументах.
В
частковому випадку, якщо величина
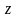залежить лише від однієї змінної z=f(x),
формула (1.13) спрощується до виду
.
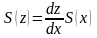(1.14)
Задача 4. Знайти середньоквадратичне відхилення результату непрямих вимірювань, якщо задані середньоквадратичні відхилення величин, отриманих прямими вимірюваннями, та функціональна залежність між величинами. Вихідні дані – з табл.10.
Таблиця 10
№ вар. |
Вид залежності |
|
|
|
3 |
|
Q=0,5см3/с S(Q)=0,005см3/с |
d=0,4cм S(d)=0,01см |
z=6,1 cм S(z)=0,1 см |
Знайдемо часткові похідні:
∂μ/∂Q=1/((3.14*(0.4)^2)/4*(2*9.8*6.1)^0.5)=0.728144
∂μ/∂d=-2*0.5/((3.14*(0.4)^3)/4*(2*9.8*6.1)^0.5)=-1.82036
∂μ/∂z=-0.5/((3.14*(0.4)^2)/4*(2*9.8)^0.5*(6.1)^(3/2))=-0.02984
За формулою 1.13
S(z)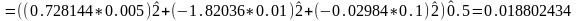
Відповідь: S(z)=0.018802434