
- •Топ, сақина, өріс туралы түсініктер, операциялардың қарапайым қасиеттері және мысалдар.
- •2. Комплекс сандар. Комплекс санның тригонометриялық түрі.
- •3. Муавр формуласы. Комплекс санның n-дәрежелі түбірін есептеу.
- •4. Матрицалар және оларға амалдар қолдану. Квадрат матрицалар.
- •5. Алмастыру мен қойылым. Инверсия, транспозиция ұғымдары. Алмастыру мен қойылымның жұп-тақтығы.
- •6. Анықтауыштар және олардың қасиеттері.
- •7. Минор. Алгебралық толықтауыш. Кері матрица. Матрицалық теңдеу.
- •8. Сызықтық алгебралық теңдеулер жүйесі. Гаусс әдісі. Крамер ережесі.
- •9. Матрицаның рангісі. Көпмүшеліктер. Көпмүшеліктерді қалдықпен бөлу. Горнер схемасы.
- •10. Евклид алгоритмі. Көпмүшеліктің түбірлері, түбірдің еселігі.
- •11. Сызықтық кеңістік. Векторлар жүйесінің сызықтық тәуелділігі. База, өлшемділік. Берілген базадағы вектор координаталары. Басқа базаға көшу.
- •12. Сызықтық қабықшалар және векторлар жүйелерінің базасы. Ішкі кеңістіктер қиылысуы мен қосындысы.
- •13. Евклид кеңістігі. Ортогоналдау процесі. Коши-Буняков теңсіздігі. Ортогоналды толықтауыш. Вектор нормасы, векторлар арасындағы бұрыш.
- •14. Сызықтық операторлар. Оператордың меншікті мәні мен меншікті векторы.
- •15. Квадраттық формалар. Инерция заңы. Оң анықталған квадраттық формалар. Сильвестр белгісі.
4. Матрицалар және оларға амалдар қолдану. Квадрат матрицалар.
$$$072
Матрицаларға келесі амалдар қолдануға болады:
A) қосу
B) бөлу
C) қатар бойынша жіктеу
D) бір біріне көбейту
E) баған бойынша жіктеу
F) санға көбейту
G) бас диагоналі бойынша жіктеу
H) қосымша диагоналі бойынша жіктеу
{Дұрыс жауаптары}=A,D,F
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$073
Матрицаны транспонирлеу дегеніміз
A) қатарлар мен бағандардың орнын аустыру
B) бағандар мен қатарлардың орнын аустыру
C) қатар бойынша жіктеу
D) бір біріне көбейту
E) баған бойынша жіктеу
F) санға көбейту
G) бас диагоналі бойынша жіктеу
H) қатарларын бағандарға жазу және бағандарын қатарлардың орнына жазу
{Дұрыс жауаптары}=A,B,H
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$074
Екі матрицаны қосу үшін
A) олардың қатарлар саны тең болуы жеткілікті
B) олардың қатарлар мен бағандар саны сәйкес тең болуы керек
C) олардың бағандар саны тең болуы жеткілікті
D) екі қатары тең болуы керек
E) олардың бағандар мен қатарлар саны сәйкес тең болуы керек
F) екі бағаны тең болуы керек
G) өлшемділіктері тең болуы керек
H) барлық элементтері тең болуы керек
{Дұрыс жауаптары}=B,E,G
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$075
Матрицаны санға көбейту үшін
A) бірінші қатарын сол санға көбейтеміз
B) олардың қатарлар мен бағандар саны сәйкес тең болуы керек
C) бірінші бағанын сол санға көбейтеміз
D) екі қатарын сол санға көбейтеміз
E) матрицаның барлық элементтерін сол санға көбейтеміз
F) матрицаның әр элементін сол санға көбейтеміз
G) матрицаның әр қатарын сол санға көбейтеміз
H) бас диагоналін сол санға көбейтеміз
{Дұрыс жауаптары}=E,F,G
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$076
Екі матрицаны көбейту үшін
A) біріншінің қатарлар саны екіншінің бағандар санына тең болуы керек
B) олардың қатарлар мен бағандар саны сәйкес тең болуы керек
C) біріншінің бағандар саны екіншінің қатарлар санына тең болуы керек
D) бағандар саны тең болуы керек
E) қатарлар саны тең болуы керек
F) екеуі бір өлшемді квадрат болуы жеткілікті
G) екі бағаны тең болуы керек
H)
біріншісі
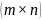 -өлшемді
болса, екіншісі
-өлшемді
болса, екіншісі
 -өлшемді
болуы қажет
-өлшемді
болуы қажет
{Дұрыс жауаптары}=C,F,H
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$077

A)
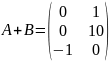
B)
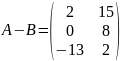
C)

D)
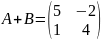
E)
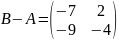
F)

G) мен
мен
 -ны
көбейтуге болмайды
-ны
көбейтуге болмайды
H)
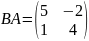
{Дұрыс жауаптары}=A,B,G
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$078

A)

B)
C)
D)
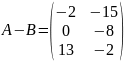
E) мен -ны көбейтуге болады
F)
G) мен -ны көбейтуге болмайды
H)
{Дұрыс жауаптары}=B,D,G
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$079
A)
B)
C)
D)
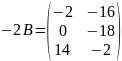
E) мен -ны көбейтуге болады
F)

G)
H) мен -ны көбейтуге болмайды
{Дұрыс жауаптары}=D,F,H
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
