Топ, сақина, өріс туралы түсініктер, операциялардың қарапайым қасиеттері және мысалдар.
$$$001
– топ,
ал
оның нормаланған ішкі тобы болсын. Онда
A) Бұл ішкі топ абелдік болады
B)
C) Алмастырулар n элементті жиыннан n элементті жиыннға съюрективті, бірақ инъективті емес бейнелеулер
D)
Алмастырулар n элементті жиыннан n
элементті жиыннға инъективті, бірақ
съюрективті емес бейнелеулер
E)
F)
G)
H)
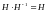
{Дұрыс жауаптары}=В,E,H
{Күрделілігі}=C
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$002
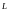– векторлық
кеңістік, ал
,
0 – нөлдік вектор болса, онда
A) абелдік топ
B) абелдік топ емес
C)
D)
E)
F)
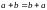
G)
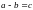
H)
{Дұрыс жауаптары}=А.D,F
{Күрделілігі}=C
{Оқулық}= Бадаев С.А. Сызықтық алгебра және аналитикалық геометрия. 1-ші,2-ші және 3-ші бөлімдер
$$$003
– векторлық
кеңістік, ал
,
– нөлдік вектор
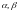скалярлар болса, онда
A) сақина болады
B) абелдік топ емес
C)
кез келген
векторы үшін
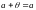
D)
E)
F)
кез келген
векторы үшін
G)
H)
{Дұрыс жауаптары}=C.D,F
{Күрделілігі}=C
{Оқулық}= Бадаев С.А. Сызықтық алгебра және аналитикалық геометрия. 1-ші,2-ші және 3-ші бөлімдер
$$$004
– векторлық кеңістік, ал , – нөлдік вектор скалярлар болса, онда
A) сақина болады
B) абелдік топ емес
C)
кез келген
векторы үшін
D)
E)
F)
кез келген
векторы үшін
G)
H)
{Дұрыс жауаптары}=C.D,F
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра және аналитикалық геометрия. 1-ші,2-ші және 3-ші бөлімдер
$$$005
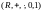– коммутативті
сақина және
болса, онда
A)
B)
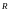қосу амалына қарағанда абелдік топ емес
C) кез келген векторлары үшін
D) қосу және көбейту амалдарына қарағанда өріс болады
E)
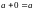
F) сақинаның кез келген элементіне кері элемент бар
G)
H)
{Дұрыс жауаптары}=А,C.Е
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра және аналитикалық геометрия. 1-ші,2-ші және 3-ші бөлімдер
2. Комплекс сандар. Комплекс санның тригонометриялық түрі.
$$$006
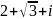комплекс
санының аргументі
A)
B)
C)
D)
E)
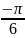
F)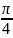
G)
H)
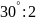
{Дұрыс жауаптары}=C,G,H
{Күрделілігі}=C
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$007
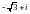санының
тригонометриялық түрі.
A)
B)
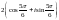
C)
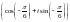
D)
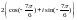
E)
F)
G)
H)
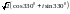
{Дұрыс жауаптары}=B,D, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$008
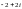санының
тригонометриялық түрі.
A)
B)
C)
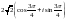
D)
E)
F)
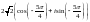
G)
H)
{Дұрыс жауаптары}=C,F, H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$009
санының
тригонометриялық түрі.
A)
B)
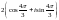
C)
D)
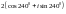
E)
F)
G)
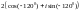
H)
{Дұрыс жауаптары}=B,C,G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$010
-
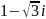комплекс саны берілген, онда оның
аргументі
A)300
B) 4/3
C) /3
D) -2/3
E) 2400
G) -5/3
H) 3300
D) 600
F) –600
{Дұрыс жауаптары}=В,D, Е
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$011
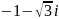комплекс
саны берілсе, оңда оның модулі
A) 2
B)
C)
D) 3
F) 4
E)
G)[1, 2.2] аралығында
H) оң сан
{Дұрыс жауаптары}=A, G, H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$012
комплекс
саны берілген, онда оның аргументі
орналасқан ширек
A)1-ші
B) 2-ші
C) [2700,3600 ]
D) [3/2, 2 ]
E) 3-ші
F) [/6, ]
G) 4-ші
H) [1800,2700 ]
{Дұрыс жауаптары}=С,D, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$013
комплекс
саны берілген, онда оның аргументі
орналасқан ширек
A)1-ші
B) 2-ші
C) [2700,3600 ]
D) [3/2, 2 ]
E) 3-ші
F) [, 3/2 ]
G) 4-ші
H) [1800,2700 ]
{Дұрыс жауаптары}=E,F, H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$014
комплекс
саны берілген, онда оның аргументі
орналасқан ширек
A)1-ші
B) 2-ші
C) [900,1800 ]
D) [/2, ]
E) 3-ші
F) [, 3/2 ]
G) 4-ші
H) [1800,2700 ]
{Дұрыс жауаптары}=B,C, D
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$015
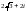комплекс
саны берілген, онда оның аргументі
орналасқан ширек
A)1-ші
B) 2-ші
C) [2700,3600 ]
D) [3/2, 2 ]
E) 3-ші
F) [0, /2 ]
G) 4-ші
H) [00,900 ]
{Дұрыс жауаптары}=A,F, H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$016
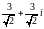комплекс саны берілген, онда оның
аргументі
A)450
B) 4/3
C) /4
D) -2/3
E) 450
F) –600
G) 2/8
H) 00
{Дұрыс жауаптары}=A,C, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$017
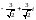комплекс саны берілген, онда оның
аргументі
A)300
B) 3/4
C) /4
D) -2/3
E) 1350
F) –600
G) -5/4
H) [00,900 ]
{Дұрыс жауаптары}=B,E, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$018
комплекс саны берілген, онда оның
аргументі
A)300
B) 3/4
C) 7/4
D) -2/3
E) 3150
F) –450
G) -5/4
H) [00,600 ]
{Дұрыс жауаптары}=C,E,F
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$019
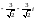комплекс саны берілген, онда оның
аргументі
A)2250
B) 3/4
C) 7/4
D) 5/4
E) 3150
F) –450
G) -5/4
H) -3/4
{Дұрыс жауаптары}=A,D,H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$020
комплекс саны берілген, онда оның аргументі орналасқан ширек
A)1-ші
B) 2-ші
C) [2700,3600 ]
D) [3/2, 2 ]
E) 3-ші
F) [0, /2 ]
G) 4-ші
H) [00,900 ]
{Дұрыс жауаптары}=C,D, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$021
комплекс саны берілген, онда оның аргументі орналасқан ширек
A)1-ші
B) 2-ші
C) [1800,2700 ]
D) [3/2, 2 ]
E) 3-ші
F) [, 3/2 ]
G) 4-ші
H) [00,900 ]
{Дұрыс жауаптары}=C,E, F
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$022
комплекс саны берілген, онда оның аргументі
A)0
B) 5/3
C) /3
D) -/3
E) 3000
G) -5/3
F) –300
H) 3300
D) 600
H) 3300
{Дұрыс жауаптары}=В,D, Е
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$023
комплекс саны берілсе, оңда оның модулі
A)
B)
C)
D) 2
F) 4
E)
G)[1, 2.2] аралығында
H) оң сан
{Дұрыс жауаптары}=D, G, H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$024
комплекс саны берілген, онда оның аргументі орналасқан ширек
A)1-ші
B) 2-ші
C) [2700,3600 ]
D) [3/2, 2 ]
E) 3-ші
F) [/2, ]
G) 4-ші
H) [1800,2700 ]
{Дұрыс жауаптары}=С,D, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$025
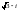санының
тригонометриялық түрі.
A)
B)
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=А,D, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$026
комплекс
санының модулін, аргументін және
координаталық жазықтықтың қай ширегінде
орналасқанын тап.
A) I-ші ширекте
B)бәрі дұрыс емес
C)II-ші ширекте
D) модулі 2-ге
E) модулі 4-ке тең
F) аргументі 1200
G) аргументі 1500
H) модулі 0-ге тең
{Дұрыс жауаптары}=C,D,F
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 .
$$$027
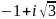комплекс
санының аргументі
A)
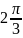
B)
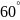
C)
D)
E)
F)
G)
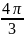
H)
{Дұрыс жауаптары}=A,D,H
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$028
комплекс санының модулі
A) 12:6
B)
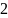
C)
D)
E)
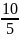
F)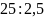
G)
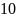
H)
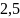
{Дұрыс жауаптары}=A,B,E
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$029
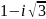комплекс
санының аргументі
A)
B)
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=A,B,E
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$030
комплекс санының модулі
A)
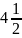
B)
C)
D)
E)
F)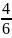
G)
H)
{Дұрыс жауаптары}=A,B,E
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$031
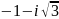комплекс
санының аргументі
A)
B)
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=A,D,H
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$032
комплекс санының модулі
A)
B)
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=A,B,E
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$033
комплекс
санының аргументі
A)
B)
C)
D)
E)
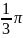
F)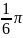
G)
H)
{Дұрыс жауаптары}=A,B,E
{Күрделілігі}=B
{Учебник}=Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$034
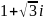комплекс
санының модулі
A)
B)
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=A,B,E
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$035
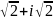комплекс
санының аргументі
A)
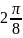
B)
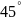
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=A,B,F
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$036
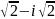комплекс
санының аргументі
A)
B)
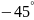
C)
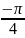
D)
E)
F)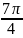
G)
H)
{Дұрыс жауаптары}=B,C,F
{Күрделілігі}=B
{Учебник}=Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$037
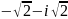комплекс
санының аргументі
A)
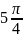
B)
C)
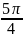
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=A,C,H
{Күрделілігі}=B
{Учебник}=Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$038
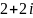комплекс
санының аргументі
A)
B)
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=A,B,F
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$039
комплекс санының модулі
A)
B)
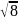
C)
D)
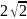
E)
F)
G)
H)
{Дұрыс жауаптары}=A,B,D
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$040
комплекс
санының модулі
A)
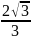
B)
C)
D)
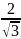
E)
F)
G)
H)
{Дұрыс жауаптары}=A,D,E
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$041
комплекс санының аргументі
A)
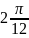
B)
C)
D)
E)
F)
G)
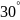
H)
{Дұрыс жауаптары}=A,C,G
{Күрделілігі}=B
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010 ;
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1978.
$$$042
санының тригонометриялық түрі.
A)
B)
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=А,D, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$043
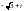санының
тригонометриялық түрі.
A)
B)
C)
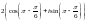
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=С,D, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$044
санының
тригонометриялық түрі.
A)
B)
C)
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=С,D, F
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$045
санының тригонометриялық түрі.
A)
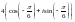
B)
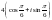
C)
D)
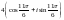
E)
F)
G)
H)
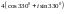
{Дұрыс жауаптары}=А,D, H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$046
санының тригонометриялық түрі.
A)
B)
C)
D)
E)
F)
G)
H)
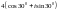
{Дұрыс жауаптары}=B,E, H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$047
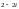санының
тригонометриялық түрі.
A)
B)
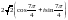
C)
D)
E)
F)
G)
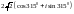
H)
{Дұрыс жауаптары}=B,C, G
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$048
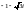санының
тригонометриялық түрі.
A)
B)
C)
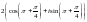
D)
E)
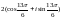
F)
G)
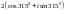
H)
{Дұрыс жауаптары}=B,C, H
{Күрделілігі}=А
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$049
арқылы
санына түйіндес санды белгілейміз. Егер
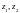комплекс сандар болса, онда
A)
B)
C)
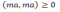
D)
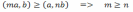
E)
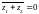
F)
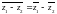
G)
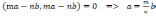
H)
{Дұрыс жауаптары}=B,C,F
{Күрделілігі}=В
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$050
арқылы
санына түйіндес санды белгілейміз. Егер
комплекс сандар болса, онда
A)
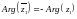
B)
C)
D)
E)
F)
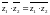
G)
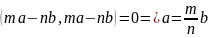
H)
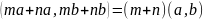
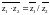
{Дұрыс жауаптары}=A,F,G
{Күрделілігі}=С
{Оқулық}= Бадаев С.А. Сызықтық алгебра және аналитикалық геометрия. 1-ші,2-ші және 3-ші бөлімдер
$$$051
Егер комплекс сандар болса, онда
A)
B)
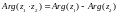
C)
D)
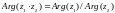
E)
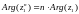
F)
G)
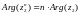
H)
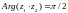
{Дұрыс жауаптары}=А,C,G
{Күрделілігі}=С
{Оқулық}= Бадаев С.А. Сызықтық алгебра мен аналитикалық геометрия:оқу құралы, 1-ші, 2-ші және 3-ші бөлімдер – Алматы: Қазақ университеті, 2010
$$$052
арқылы
санының модулін,
арқылы
санына түйіндес санды белгілейміз. Егер
комплекс сандар болса, онда
A)
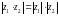
B)
C)
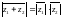
D)
E)
F)
G)
H)
{Дұрыс жауаптары}=A,D,H
{Күрделілігі}=С
{Оқулық}= Бадаев С.А. Сызықтық алгебра және аналитикалық геометрия. 1-ші,2-ші және 3-ші бөлімдер
$$$053
арқылы санының модулін, арқылы санына түйіндес санды белгілейміз. Егер комплекс сандар болса, онда
A)
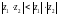
B)
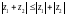
C)
D)
E)
F)
G)
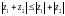
H)
{Дұрыс жауаптары}=B,E,G
{Күрделілігі}=С
{Оқулық}= Бадаев С.А. Сызықтық алгебра және аналитикалық геометрия. 1-ші,2-ші және 3-ші бөлімдер