2. Спектральна теорема для компактного самоспряженого оператора.

Лема 1. 1) Власні значення самоспряженого оператора А L (Н) – дійсні числа. 2) Різним власним значенням оператора А = А відповідають ортогональні власні вектори.

Довести самостійно.

Означення. Підпростір називається інваріантним для оператора А L (Н), якщо .

Лема. Якщо G – інваріантний підпростір для оператора А L (Н), то G є інваріантний підпростір для оператора А .

Довести самостійно.

Теорема. Нехай А – компактний самоспряжений оператор в Н, - сукупність всіх ненульових власних значень А, Р( ) – ортопроектор на власний підпростір . Для кожного х маємо представлення , де ряд збігається в нормі Н. Крім того, .

Доведення. Згідно з теоремою у А є власний вектор , що відповідає власному значенню ( ), тобто множина ₵} і Ø. Підпростір Н = інваріантний для самоспряженого оператора А. Візьмемо звуження оператора А на Н , будемо мати самоспряжений компактний оператор А , що діє в Н . Якщо А = 0, то теорема доведена. У противному випадку А має власний вектор , що відповідає власному значенню ( ). Зазначимо, що . Дійсно, з нерівності , отже .

Якщо , то в Н існує послідовність {x } така, що . Як і в доведенні першої теореми, в Н будемо мати власний вектор оператора А, що відповідає власному значенню , а це не можливо.

Згідно з попередньою лемою . Покладемо Н = , Н інваріантно для А, нехай А звуження А на Н . Якщо А = 0, то теорема доведена, у противному випадку продовжимо далі. Покладемо = . Всі власні вектори А, що відповідають не нульовим власним значенням , належать Н, отже = Ker A (в другому випадку у підпросторі знайдеться власний вектор А, що відповідає власному значенню не рівному нулю, а це суперечить означенню ). Таким чином, має місце розклад, що вказаний в умові теореми, звідки випливає і друга рівність.

Лекція 12. Розклад одиниці. Спектральні інтеграли та спектральний розклад обмеженого самоспряженого оператора.

1. Розклад одиниці.

Нехай R абстрактний простір, R деяка - алгебра множин з R. Крім того Н – гільбертовий простір.

Означення. Операторозначна функція R Е ( ) L (Н) називається розкладом одиниці (на R), якщо виконуються вимоги:

1. R Е ( ) – ортопроектор в Н; Е( Ø ) = 0, Е(R) = Е;

2. для будь – якої послідовності таких, що R ( і ) і = Ø (i j), виконується , де ряд збігається на кожному векторі f Н по нормі Н.

Зауважимо, що якщо R Е ( ) – розклад одиниці, то для фіксованого f Н, функція множин R ( ) = (Е ( )f, f) = буде мірою на R.

Крім того, при фіксованих f, g H функція множин R w ( ) = (Е ( )f, g) C буде комплексним зарядом на R (вона є лінійною комбінацією мір, що випливає з полярізаційной рівності).

Приклади. 1. Нехай R = R , деяка послідовність точок з R , (Р ) – послідовність проекторів в Н така, що . У якості R візьмемо, наприклад, B (R ) і покладемо R . Сукупність Е( ) – розклад одиниці.

Зауважимо, що компактний самоспряжений оператор породжує такий розклад одиниці, що відповідає сукупності його власних значень.

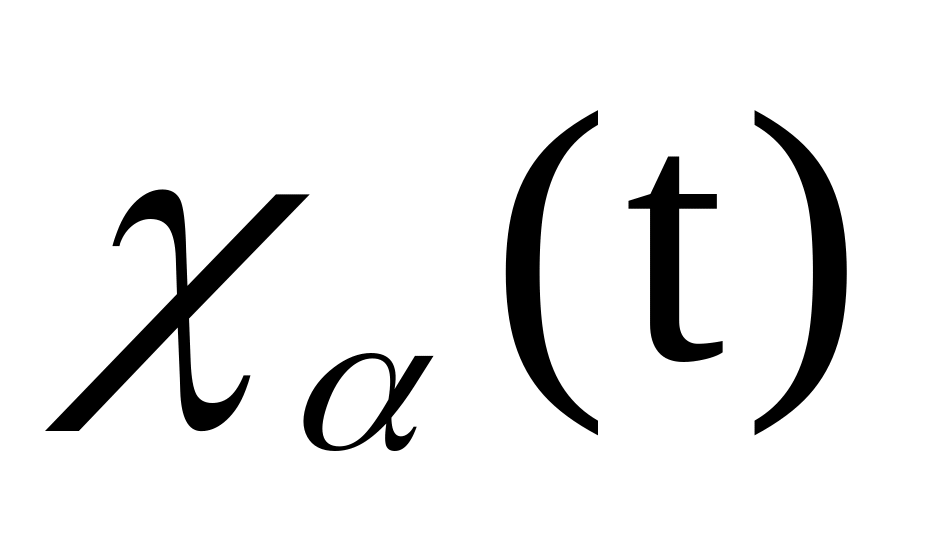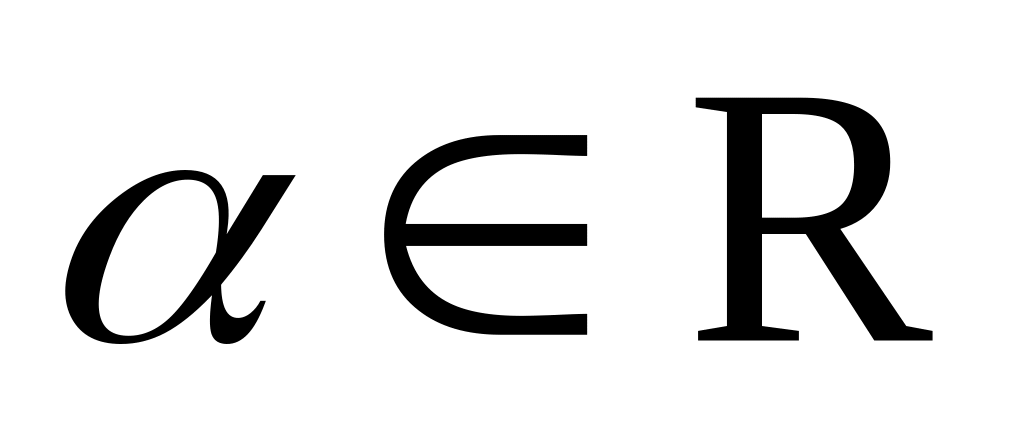2. Нехай (R, R), довільний простір, μ деяка міра на ньому. Покладемо Н = L (R, dμ) і розглянемо в L (R, dμ) оператор Е( ) – як оператор множення на - індикатор множини , т.п. (Е ( )f )(t) = f(t).

Тоді Е ( ) = Е( ), Е ( ) = Е( ), Е( ) L (Н). Тобто Е( )- ортопроектор. - адитивність розкладу одиниці випливає з - адитивності інтеграла Лебега.