17.Знакопостоянные ряды. Сравнительные признаки сходимости.

Ряд называется знакопеременным, если он имеет бесконечное число как положительных, так и отрицательных членов.

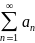Ряд называется абсолютно сходящимся, если сходится абсолютный ряд .

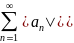Если ряд сходится, то и ряд сходится.

Ряд называется условно сходящимся, если абсолютный ряд расходится, а исходный ряд сходится.

Сравнительные признаки сходимости.

Даны два ряда и − такие, что для всех n. Тогда справедливы следующие признаки:

1)Если сходится, то также сходится;

2)Если расходится, то также расходится.

Предельные признаки сравнения рядов

Пусть даны два ряда и , у которых члены a_n и b_n положительны для всех n. Тогда справедливы следующие предельные признаки:

Если , то оба ряда и либо сходятся, либо расходятся;

Если , то ряд сходится, если сходится ряд ;

Если , то ряд расходится, если расходится ряд .

Так называемый обобщенный гармонический ряд сходится при p > 1 и расходится при 0 < p ≤ 1.

18.Признак Даламбера. Интегральный признак сходимости.

Признак Даламбера.

Пусть для положительного ряда существует предел .

Тогда:

1. если q<1, то ряд сходится;

2. если q>1, то ряд расходится;

3. если q=1, то вопрос о сходимости остается открытым.

Интегральный признак сходимости.

Если функция f(x) неотрицательна и убывает на промежутке [a,+∞), где a≥1, то ряд и интеграл сходятся и расходятся одновременно.

19. Знакочередующиеся ряды. Признак Лейбница.

(Теорема Римана) При перестановке членов условно сходящегося ряда можно получить ряд, имеющий заранее заданную сумму, и даже расходящийся ряд. Числовой ряд называется знакочередующимся, если для любого nчлены ряда и 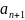имеют разные знаки. Ряд можно записать в виде: , >0.

Признак Лейбница: пусть для знакочередующегося ряда выполнены условия: 1. Последовательность является невозрастающей. 2. =0 , тогда ряд сходится.

20. Знакопеременные ряды. Достаточный признак сходимости. Абсолютно и условно сходящиеся ряды.

Ряд называется знакопеременным, если он имеет бесконечное число как положительных так и отрицательных членов. Ряд называется абсолютно сходящимся , если сходится абсолютный ряд . Если ряд сходится, то и ряд сходится.

Ряд называется условно сходящимся, если абсолютный ряд расходится , а исходный ряд сходится.

21. Степенные ряды. Область сходимости степенного ряда.

Ряд вида , где -действительные части , называется степенным рядом по степеням ( x- ).

Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости R:

| x-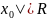 или

Сходимость ряда на границах (при ) необходимо исследовать дополнительно.

Радиус сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле

R=

или на основе признака Даламбера:

R=

22. Теорема Абеля. Интегрирование и дифференцирование степенных рядов.

Если степенной ряд ( сходится в точке , то он сходится в абсолютно в интервале, соответствующим неравенству

Если в точке степенной ряд расходится , то он расходится во всех точках x таких , что

Если степенной ряд сходится хотя бы в одной точке , то всегда существует число такое, что степенной ряд сходится абсолютно для всех и расходится для всех

Функция является непрерывной функцией при |x| <R. Степенной ряд внутри интервала сходимости можно дифференцировать почленно. При этом производная степенного ряда выражается формулой

Степенной ряд можно также почленно интегрировать на отрезке, который расположен внутри интервала сходимости. Следовательно, если − R < b < x < R, то выполняется равенство

Если ряд интегрируется на отрезке [0; x], то справедлива формула: