
- •Ответы по теории к экзамену по дисциплине «Математический анализ»
- •1.Понятие определенного интеграла. Понятие интегральной суммы, предел интегральной суммы. Геометрический, физический и экономический смысл.
- •2.Необходимые условия, достаточные условия существования, свойства определенного интеграла.
- •3.Определенный интеграл как функция верхнего предела. Формула Ньютона – Лейбница.
- •4. Замена переменной в определенном интеграле. Интегрирование по частям в определенном интеграле.
- •5.Несобственные интегралы первого и второго рода. Признаки сходимости несобственных интегралов.
- •6.Геометрические приложения определенного интеграла. Вычисление площадей и объемов тел вращения.
- •7.Дифференциальные уравнения. Виды дифференциальных уравнений. Существование и единственность решения дифференциального уравнения первого порядка.
- •8.Общее решение дифференциального уравнения. Семейства интегральных кривых, фазовый портрет. Особые точки.
- •9. Дифференциальные уравнения первого порядка. Неполные дифференциальные уравнения.
- •10.Уравнения с разделяющимися переменными.
- •11.Однородные дифференциальные уравнения первого порядка. Линейные уравнения первого порядка.
- •12.Уравнение Бернулли. Уравнения в полных дифференциалах.
- •13.Дифференциальные уравнения n-го порядка. Уравнения, допускающие понижение порядка.
- •14.Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •15 .Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •16.Основные понятия числовых рядов. Свойства сходящихся рядов.
- •17.Знакопостоянные ряды. Сравнительные признаки сходимости.
- •18.Признак Даламбера. Интегральный признак сходимости.
- •19. Знакочередующиеся ряды. Признак Лейбница.
- •20. Знакопеременные ряды. Достаточный признак сходимости. Абсолютно и условно сходящиеся ряды.
- •21. Степенные ряды. Область сходимости степенного ряда.
- •22. Теорема Абеля. Интегрирование и дифференцирование степенных рядов.
- •23. Ряд Тейлора. Применение рядов в приближенных вычислениях.
14.Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Алгоритм
нахождения общего решения линейного
однородного дифференциального уравнения
второго порядка с постоянными
коэффициентами
![]() .
p
и
q
- произвольные
действительные числа.
.
p
и
q
- произвольные
действительные числа.
Записываем характеристическое уравнение k2 + p ⋅ k + q = 0.
Находим корни характеристического уравнения k1 и k2.
В зависимости от значений корней характеристического уравнения записываем общее решение ЛОДУ с постоянными коэффициентами в виде:
 ,
если
,
если
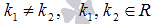 ;
;
 ,
если
,
если
 ;
;
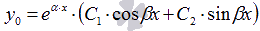 ,
если
,
если

15 .Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейное
неоднородное дифференциальное уравнение
(ЛНДУ) второго порядка с постоянными
коэффициентами имеет вид
![]() ,
где p
и q
– произвольные действительные числа,
а функция f(x)
– непрерывна на интервале интегрирования
X.
,
где p
и q
– произвольные действительные числа,
а функция f(x)
– непрерывна на интервале интегрирования
X.
1)Если
f(x)
является многочленом n-ой
степени f(x)
= Pn(x),
то частное решение ЛНДУ ищется в виде
![]() ,
где Qn(x)
– многочлен степени n,
а r
– количество корней характеристического
уравнения, равных нулю. Так как
,
где Qn(x)
– многочлен степени n,
а r
– количество корней характеристического
уравнения, равных нулю. Так как
![]() -
частное решение уравнения
,
то коэффициенты, определяющие многочлен
Qn(x),
находятся методом неопределенных
коэффициентов из равенства
-
частное решение уравнения
,
то коэффициенты, определяющие многочлен
Qn(x),
находятся методом неопределенных
коэффициентов из равенства
![]() .
.
2)
Если функция f(x)
представлена произведением многочлена
степени n
и экспоненты
![]() ,
то частное решение ЛНДУ второго порядка
ищется в виде
,
то частное решение ЛНДУ второго порядка
ищется в виде
![]() ,
где Qn(x)
– многочлен n-ой
степени, r
– число корней характеристического
уравнения, равных
,
где Qn(x)
– многочлен n-ой
степени, r
– число корней характеристического
уравнения, равных
![]() .
Коэффициенты многочлена Qn(x)
определяются из равенства
.
.
Коэффициенты многочлена Qn(x)
определяются из равенства
.
3)
Если функция f(x)
имеет вид
![]() ,
где А1
и В1
– числа, то частное решение ЛНДУ
представляется как
,
где А1
и В1
– числа, то частное решение ЛНДУ
представляется как
![]() ,
где А
и В
– неопределенные коэффициенты, r
– число комплексно сопряженных пар
корней характеристического уравнения
равных
,
где А
и В
– неопределенные коэффициенты, r
– число комплексно сопряженных пар
корней характеристического уравнения
равных
![]() .
Коэффициенты многочлена А
и В
находятся из равенства
.
Коэффициенты многочлена А
и В
находятся из равенства
4)
Если
![]() ,
то
,
то
![]() ,
где r
– число комплексно сопряженных пар
корней характеристического уравнения,
равных
,
где r
– число комплексно сопряженных пар
корней характеристического уравнения,
равных
![]() ,
Pn(x),
Qk(x),
Lm(x)
и Nm(x)
- многочлены степени n,
k,
m
и m
соответственно, m
= max(n, k).
Коэффициенты многочленов Lm(x)
и Nm(x)
находятся из равенства
.
,
Pn(x),
Qk(x),
Lm(x)
и Nm(x)
- многочлены степени n,
k,
m
и m
соответственно, m
= max(n, k).
Коэффициенты многочленов Lm(x)
и Nm(x)
находятся из равенства
.
5) Для любого другого вида функции f(x) применяется следующий алгоритм действий:
находится общее решение соответствующего линейного однородного уравнения как y0 = C1 ⋅ y1 + C2 ⋅ y2, где y1 и y2 - линейно независимые частные решения ЛОДУ, а С1 и С2 – произвольные постоянные;
варьируются произвольные постоянные, то есть, в качестве общего решения исходного ЛНДУ принимается y = C1(x) ⋅ y1 + C2(x) ⋅ y2;
производные функций C1(x) и С2(x) определяются из системы уравнений
 ,
а сами функции C1(x)
и C2(x)
находятся при последующем интегрировании.
,
а сами функции C1(x)
и C2(x)
находятся при последующем интегрировании.
16.Основные понятия числовых рядов. Свойства сходящихся рядов.
Числовой
ряд
– это сумма членов числовой
последовательности вида
![]() .
.
Частичная
сумма числового ряда
– это сумма вида
![]() ,
где n
– некоторое натуральное число.
,
где n
– некоторое натуральное число.
![]() называют
также n-ой
частичной суммой числового ряда
называют
также n-ой
частичной суммой числового ряда
Числовой
ряд
![]() называется
сходящимся,
если существует конечный предел
последовательности частичных сумм
называется
сходящимся,
если существует конечный предел
последовательности частичных сумм
![]() .
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
называется
расходящимся.
.
Если предел последовательности частичных
сумм числового ряда не существует или
бесконечен, то ряд
называется
расходящимся.
Суммой
сходящегося числового ряда
называется
предел последовательности его частичных
сумм, то есть,
![]() .
.
Свойства сходящихся рядов.
1. Члены сходящегося ряда можно умножить на одно и то же число k. Полученный ряд будет сходиться, а сумма его будет в k раз больше суммы исходного ряда.
2. Члены сходящегося ряда можно группировать. Полученный ряд будет сходиться, и сумма его не изменится.
3. В сходящемся ряде можно отбросить конечное число первых членов . Полученный ряд будет сходиться, а его сумма будет меньше суммы исходного ряда на B.
4. Для того чтобы ряд сходился необходимо и достаточно, чтобы сходился остаток ряда. (Докажите это самостоятельно, используя доказательство свойства 3).
5. Сходящиеся ряды можно складывать (или вычитать), получая сходящийся ряд с суммой, равной сумме (или разности) сумм исходных рядов.
